基于随机过程的磨料面形成方法研究

（延边大学机械工程系，吉林 延 吉 1 33002）

磨料磨损是由外界硬质颗粒或硬表面的微峰在摩擦副对偶表面相对运动过程中，引起表面擦伤与表面材料脱落的现象，也称为(磨粒磨损)。其特征是在摩擦副对偶表面沿滑动方向形成划痕。对磨料磨损的分类[1]，当前主要根据系统中是否存在第三体而分为二体磨料磨损和三体磨料磨损两种形式。由于磨料磨损问题的复杂性、材料的特性决定了磨料磨损问题不存在通用的模型，所以对磨料磨损问题的研究多依赖于从实验数据中得到特性规律，因此，对磨料磨损计算及建模有重大的实际意义。但由于对磨料磨损机理的研究还不够充分，长期以来，人们主要是利用简化模型和基于实验数据拟合的经验公式进行研究。

对磨料磨损机理的研究源于分析黏着磨损机制的Archard模型，并通过实验证明其用于磨料磨损是可行的，并且在以后关于磨料磨损的很多模型都是以Archard模型为基础的。该模型可表述为磨损率正比于载荷，磨损率与滑动速度无关，磨损率与材料硬度成反比，虽然模型存在着一定的局限性，但一直都是研究摩擦磨损的经典模型。Jacobson建立了二维的磨料磨损统计学模型，该模型在Archard磨损模型基础之上，运用随机函数，仿真了变化的磨粒高度、直径的情况下的磨损情况，但是没有考虑磨料磨损过程中，三维形状参数的随机模拟。Rabinowicz从接触力学的角度研究了单颗粒切削模型，假设磨粒形状为圆锥形，在切向力作用下，产生位移S，以犁出的沟槽推导了材料磨损率公式。该模型从力学角度对磨料磨损进行了研究，为磨料磨损有限元方法研究奠定了一定基础。

在近40年来的文献中有300多个磨损公式，但都是在特定条件下并存在很大的局限性前提下得到的[2]。在磨料磨损过程中同时存在几种机理，由于外界条件及材料组织的影响，磨损机理发生了变化，为了在模型中尽可能更多的引入参数的影响，综合磨损机理的研究，使模型更符合实际情况，把磨损过程以随机过程的方法建立数学模型，并用概率论的方法来描述和求解磨料磨损问题是可行的[3]。图1给出了磨料磨损系统中影响磨损的各种相关参数。

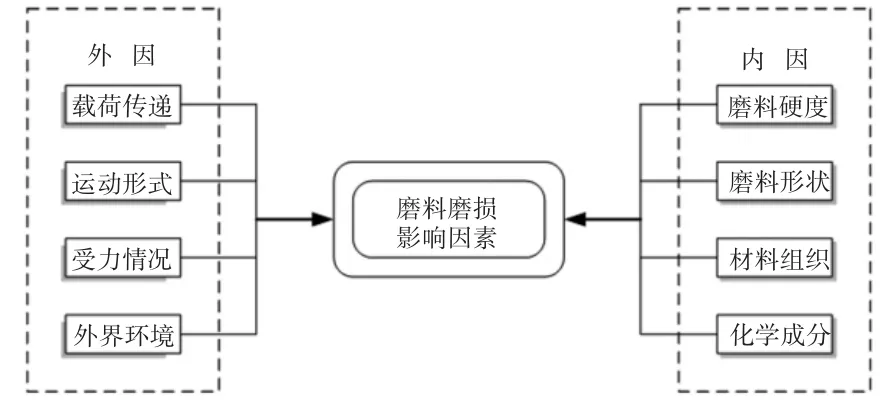
图1 磨料磨损影响因素

1 基于随机过程的磨料模型

1.1 磨粒形状确定

磨料形状的不规则性导致了无法通过确定的数值关系建立磨料模型，这就为仿真带来了很大的困难。目前主要采取简化复杂形状并将其视为简单几何体，例如圆锥、棱锥、针形等。Stachowiak通过理论和实验分析认为参与磨损的磨料压入磨损表面的部分为圆锥形状，并就此提出了“圆锥拟合分析法”并进行了计算机模拟[4]。本文考虑在实际工况中，由于磨损过程一旦发生，磨料与工件表面之间的相对运动将导致材料的塑性变形，并且发生围观材料损失现象。为了更加真实地反映磨料磨损情况，以及数学模型的可实现性这两方面因素，以圆台型磨料实现磨料面的生成。图2给出了任意形状的磨料压入情况，图3为圆台拟合磨料示意图。

图2 随机形状磨料磨损示意图

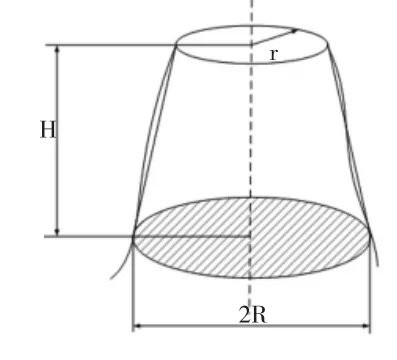
图3 圆台拟合法磨料形状

1.2 Monte Carlo方法求解磨料磨损问题

由于磨料磨损过程的不确定性和随机性，决定了对磨损问题的研究不可能通过建立确定的模型来描述，通过经验公式对数据进行拟合的方法在针对具体问题时又失去了很多特有性质，所得到的结果也是不真实的。因而通过统计学方法建立磨料磨损过程的数学模型是一种重要的方法。Monte Carlo方法是一种采用统计抽样理论近似求解数学、物理及工程问题的方法，根据Monte Carlo基本解题思路，首先应建立与磨料磨损过程相似的概率统计模型，然后进行随机模拟、求解。

文献[4]对木里图石英砂做了颗粒分布测试试验，通过对该实验数据进行统计、筛选，得到了砂子粒径呈正态分布，并就此得到粒径的平均估计量值为：0.180，标准差为：0.027。故本文中磨料的几何参数设为正态分布，在磨料面中的位置参数服从均匀分布。在图3中，磨料的相关参数确定如下：

磨料底面中心在磨料面上位置的横坐标值x：均匀分布；

磨料底面中心在磨料面上位置的纵坐标值y：均匀分布；

磨料底面半径R：正态分布；

磨料顶面半径r：正态分布；

磨料高度H：正态分布。

2 磨料面生成方法研究

2.1 磨料面随机模型

在建立磨料面模型时，需要用到正态分布和随机分布两种分布规律。在用Monte Carlo方法进行仿真的过程中，只要已知统计规律，从理论上来说就可以通过变换得到所需要的任何随机变量。而当以离散分布的随机数代替连续分布的随机数时，实际上计算机随即发生器产生的是周期性出现的伪随机数[5~6]。从表面上看和真正的随机数是违背的，但是只要我们将得到的伪随机数的数值序列数通过统计检验，就可以以此代替真正的随机数。然后利用反函数法可以将伪标准分布的随机数转换成所需要任何数值区间的正态分布和均匀分布的随机变量。

式中，

准为正态分布N（μ，σ2）的随机变量；

γ1、γ2为（0，1）之间均匀分布的随机数；

μ为正态分布N（μ，σ2）的均值。

设连续型随机变量所具有的概率密度为

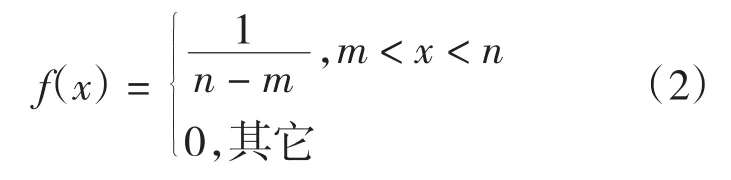
则x在区间(m，n)上服从均匀分布，要得到该区间上的随机数，将(0，1)区间的均匀分布的随机数的区间变换为(m，n)，有

式中，

φ为区间(m，n)上均匀分布的随机变量；

γ为(0，1)之间均匀分布的随机数。

通过上述关系的建立，从数学关系上可以实现磨料磨损过程中磨料参数的随机实现，真实地反映了磨料的分布情况。并且通过检验区间(0，1)上的均匀分布的参数是否显著，以此来验证数学模型的可行性。

2.2 磨料面生成算法研究

当磨料随机模型的参数确定后，需要考虑磨料在磨料面上的分布情况。磨料面的生成包括磨料本身几何参数及磨料和平面之间的相对位置，以计算机模拟磨料面的生成需要算法实现在平面上的取点，并且放置新的磨料时候，需要去除上一磨料所占用的区域。除此之外，还要考虑具体的磨料的面密度情况来实现磨料的疏密程度，尽可能的避免磨料之间的重叠现象。本文以打靶法实现了磨料在磨料面上的取点，以圆台型磨料底面位置参数作为程序控制点，首先指定第一点坐标(x1，y1)及底面直径D1，并判断该点是否处在所处的区域内，如果是则存储该点参数值到预定义的结构单元中，反之，则重新生成随机点坐标及参数。在产生第二点坐标(x2，y2)及底面直径D2时，判断第二点是否在指定区域内，而且需要判断第二点是否与第一点存在相交区域，如果两个条件都满足则存储第二点到结构体中，以此进行直到达到所要求磨料密度值为止，图4为磨料在磨料面上找点算法图示。

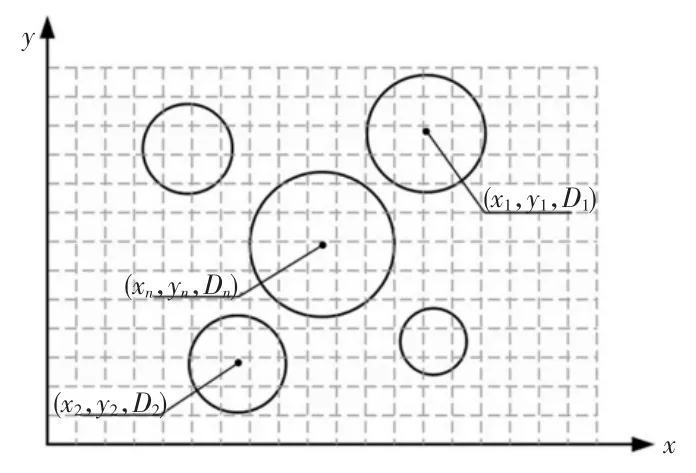
图4 磨料位置求点算法图示

3 仿真实例验证

通过对给定数值的磨料参数进行统计检验，使相对误差控制在0.3%以内，该方法在工程上是可行的。为了更准确的验证该方法在磨料磨损仿真应用上的可靠性，以MatLab软件为平台，利用MatLab自带图形函数并编写算法程序实现了图5所示的磨料面形貌，可以对磨料面进行三维观察。图中给出了3.0×3.0 mm范围内的磨料表面。

图5 磨料面仿真形貌

4 结束语

本文研究了磨料磨损过程中磨料面的形成规律，并利用统计学的方法对磨料的参数进行了建模，并以MatLab软件为平台编程仿真了磨料面的形成。通过仿真结果可以看出该方法为磨料磨损的仿真研究提供了方便、快捷及有效的手段。在以后的学习中将以此为基础，进行磨料磨损过程的仿真、有限元模型的研究。

[1]赫罗绍夫，巴比切夫.金属的磨损[M].北京:机械工业出版社，1996.

[2]欧阳习科，蒋业华，周 荣.磨料磨损理论发展[J].水利电力机械，2004,26(6):25-28.

[3]D.V.De Pellegrin,G.W.Stachowiak.Simulation of three-dimensional abrasive particles[J].Wear，2005,258(26):208-216.

[4]吴国清，张晓峰，方 亮，邢建东.两体磨料磨损的三维动态模拟[J].摩擦学学报，2000,20(5):360-364.

[5]Staffan Jacobson,Per Wallén,Sture Hogmark.Fundamental aspects of abrasive wear studied by a new numerical simulation model[J].Wear，1988,123(2):207-223.

[6]M.Barge,G.Kermouche,P.Gilles,J.M.Bergheau.Experimental and numerical study of the ploughing part of abrasive wear[J].Wear，2003,255(6):30-37.