公交专用道对车辆间隔时间的影响分析

顾天鸿， 吴世迪

(大连科技学院 机械工程系，辽宁 大连 116052)

0 引言

公共交通是城市客运交通的主体，然而我国绝大多数城市的公交系统都存在着准点率差，公交出行效率低的状况，实际经验表明，仅依靠拓宽道路来提高公共汽车的行驶速度，其效果并不明显。目前，很多城市都采用了公交专用道的形式，通过设置一些特定的专用道来让公共汽车享有更多的优先权，以提高公共交通车辆的行驶速度和运行准点率，鼓励公众使用公交出行方式，最终实现缓解交通拥挤的目的［1］。那么，公交专用道的设置对公交准点运行的影响程度究竟怎样，这里应用概率与统计的方法对这一问题进行了分析。

1 公交车辆到达间隔时间的调查取样

公交专用道是指在特定路段上，通过标志、标线等画出一条或几条车道供公交车专用，其他车辆不得随意驶入，同时，公交车享有在其他车道上行驶的权利［2］。设置公交专用道的目的在于给公共汽车较高等级的专用权，从而改善公共交通车辆的运行环境，提高公共交通的运输服务水平。为了研究公交专用道的设置对公交车辆准点运行情况的影响程度，现对某城市的241 路公交线路进行了调查，调查对象的基本情况如下:241 路公交线路全长6．4 km，全线设为公交专用道，沿途共设13 个车站，全程准点运行时间为20 min，发车间隔为高峰时段4 ～6 min，平峰时段5 ～8 min。

调查采用驻站的形式，时间为正常工作日的平峰时段，地点选取241 路公交线路的5 个重要且近似等距的车站，每个车站记录100 个时距(即车辆到达间隔时间)数据，共采集车辆到达间隔时间的样本数据500 个。除去受交通事故、恶劣天气等因素影响的不良数据45 个，最终得到样本有效数据共455 个，其散点图见图1。

图1 有公交专用道线路样本数据散点图

2 车辆到达间隔时间X 的概率分析

2．1 绘制样本数据直方图

确定组数。由斯特格斯经验公式:组数K = 1 + log2n，其中，n 为样本数据的个数，结果取整。当n =455 时，得K =10。

确定组距。样本数据中最小值为185，最大值为679。可认为样本数据都介于区间(180，680)之间，故组距=(680 -180)/10 =50，统计各组的频数(各组元素个数)并整理成频数分布表(表1)，画出样本数据直方图(图2)。

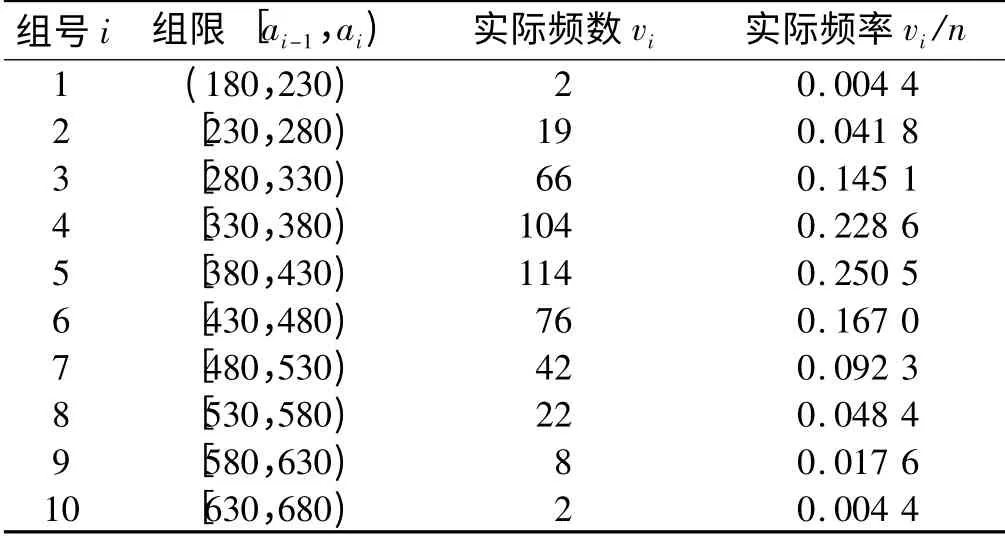
表1 样本频数分布表

图2 有公交专用道线路样本数据直方图

2．2 数据拟合

由图2 可看出，样本直方图基本上是单峰对称的，外轮廓线接近于正态分布的概率密度曲线

根据最大似然估计的方法求解正态分布中的未知参数μ，σ2为

2．3 χ2 检验

当理论分布与实际观测数据的拟合进行比较时，要求有一些评价拟合质量的方法，在交通工程中目前最为常用的是χ2检验。在满足样本量要求的前提下应用χ2进行拟合优度检验时，要求各组样本的实际频数不能小于5，若实际频数小于5 时，应将该组样本适当合并，合并后的分组情况及各组样本的实际频数见表2，检验如下:

基本假设为H0:车辆到达间隔时间X ～N(402．132，6 101．512)，由K．Pearsn 统计量［3］

式中，pi为理论概率，各计算数据见表2。

表2 χ2 检验的数据计算表

2．4 “有-无”对比分析

在对有公交专用道的公交线路进行调查取样的同时，对无公交专用道的公交线路以同样的方法进行取样，图3 为该城市240 路公交线路(无公交专用道)车辆到达间隔时间的数据散点图，对比图1 可知，在无公交专用道时车辆到达间隔时间随机性很大，说明车辆运行过程中受外界因素的干扰较大，运行准点率较低。

图3 无公交专用道线路样本数据散点图

3 结束语

由以上分析可知，有公交专用道的车辆到达间隔时间服从正态分布，且概率密度曲线的峰值集中在5 ～8 min(发车间隔时间)，说明设置公交专用道后，大部分车辆基本能够以发车间隔时间到达(概率为76．4%)，车辆在行驶过程中外界因素的干扰很小，车辆运行的准点率较高。

实际情况表明，公交专用道作为一种非常重要的公交优先措施，能够最大限度地减少行程延误，在有限的道路条件下提高公共汽车的服务水平，是创造良好交通环境的有效措施［5］。

［1］丁卫东，柳祖鹏，刘明．城市公交专用车道系统规划与设置研究［J］．交通科技，2004，205(4):96-98．

［2］裴玉龙，李洪萍，蒋贤才，等．城市交通规划［M］．北京:中国铁道出版社，2007．

［3］吴群英，林亮．应用数理统计［M］．天津:天津大学出版社，2004．

［4］朱勇华，邰淑彩，孙韫玉．应用数理统计［M］．武汉:武汉水利电力大学出版社，2000．

［5］李彬，郭冠英，杨东援． 城市公共交通专用道规划研究［J］． 合肥工业大学学报:自然科学版，1999，22(3):57-61．