调和级数与P级数敛散性简证

吴章文

（长江工程职业技术学院，武汉 430212）

1 证明调和级数是发散的

在数学的教学与学习中，学生是学习与研究的主体，也是认识与发展的主体。理想的教学过程中学生可以充分体现自主性、能动性及创造力。教学中教师的变化和灵活能促使学生对自己的学习方法不断地进行总结、评价和改进，不断修订、补充和完善，使之达成有特色的高效的学习。

从这一目的出发，下面试用不同的方法讨论调和级数。证法1：

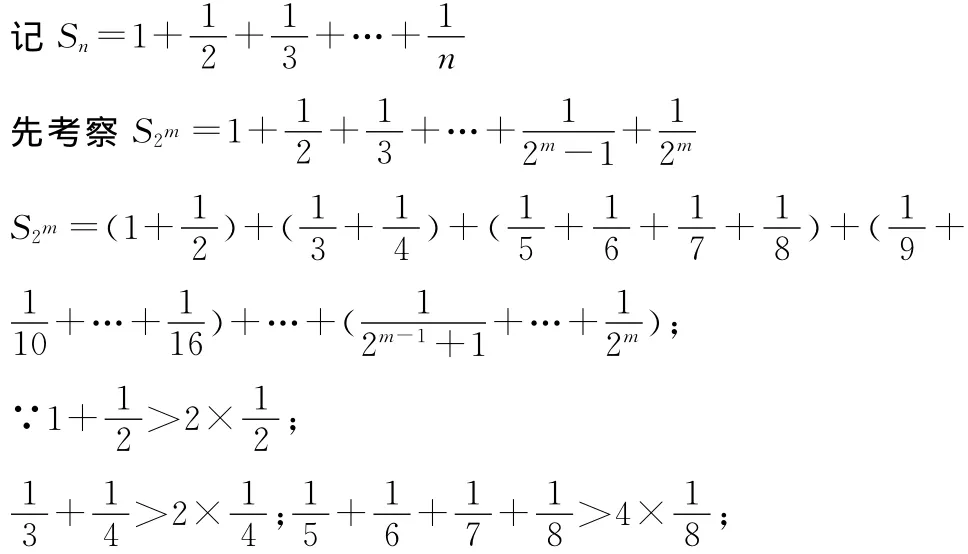
问题已经解决了，多数学生不会满足。他们在总结，反思，回顾，消化中会进一步思考。方法技巧能否改进？能否从特别到一般？有没有更高层次的数学理论与数学思想？

就数学的学习与研究而言，其中重要的一点就是要清楚地表明教学的联系和发展。教学中的灵活性，能否引发学生的积极性和创造性？教学的基础和发展往往是高度统一的。我们要有教学共通性的直觉。数学的教学过程当然也是一个发展的过程。这里我们再来论证P－级数的问题。

教学过程中，教师要让学生成为学习主体，从不同的方面去思考，去探讨不同的解决问题的思路和方法，主动地去发展数学的学习。

下面换一种方式继续讨论问题。

任一自然数n，总可以对应地找一个与n最近的自然

3 结束语

在教学中，教师要有常教常新的感觉，学生也要在学习中不断体验知识的多样性和趣味性。从引导学生学习，启迪学生智慧出发，从充实课堂内容，为教学实际服务着想，老师与学生要加强互动，讨论时不拘泥于经典和范例。这样可指导学生从不同侧面，用不同的方法技巧解决一些问题。

［1］同济大学数学系.高等数学（第6版）［M］.北京：高等教育出版社，2007：256-257.

［2］陈盛双，梅汇海.高等数学［M］.武汉：武汉理工大学出版社，2010：290-291.

［3］Cohen and Knight.P级数敛散性的一个简单证法［J］.数学通报，1982，（5）：31-32.

［4］华科技大学高等数学课题组.微积分［M］.武汉：华中科技大学出版社，2001：430-432.

［5］华罗庚.高等数学引论（第1卷第1分册，第5版）［M］.北京：科学出版社，1979：221-223.