应用标签域的贝叶斯网络图像分割算法
2013-02-09李鹏
李 鹏
(长江大学 计算机科学学院,湖北 荆州434023)
0 引 言
图像分割是一种常见的图像处理过程中的预处理过程,其中包括基于区域的紧凑图像场景描述,可将它分解成具有相似属性的空间相关区域来进行实现[1-2]。此类底层视觉任务往往是许多图像理解算法和计算机视觉应用的起始步骤,同时也是重要的预处理步骤[3-4]。
本文提出的图像分割方法在理论上与文献 [5]是有区别的,它不是考虑复杂质感设计的自然图像分割模型,本文探讨用来进行替换的融合 (即有效结合形式)进行快速估计的图像分割模型,从而能够最终得到可靠准确的图像分割结果。文献 [6]中在概念上增加有区别的标签领域融合模型,并提出混合空间图像分割目标和快速估计应用领域 (例如运动估计/字段分割、封闭图像等)。目标融合过程的相关解释是在于当地融合的标签领域涉及两个不同性质标签在不同的抽象层次 (即逐像素、逐区域)。更确切的说,它的目标是以迭代形式来修改相关应用领域,使其区域适合的颜色区域进行空间分割与假设颜色分割比的应用领域的区域更详细。在这种方式中,错误分类的像素中应用领域过滤并锐化blobby形状,并产生更精确的最终应用标签字段。
1 相关融合模型
1.1 概率等级索引
概率等级索引 (probabilistic rand index,PRI)是由Unnikrishnan[7]提出的新概念,它考虑在人类观察者之间可能的解释固有变化的图像,即多个可接受的地面真像与每个自然图像之间进行的图像分割。最近文献 [8]指出观察者之间的这种变化在Berkeley分割数据集上得到体现。其实,每个人在不同程度上选择的图像分割都有区别。这种变化是由于图像分割是高斯法问题,不同可能值的数量对应Apriori应具有多种解决方案。
因此,在特有的地面真像进行分割的情况下,对聚类质量进行度量是具有自动量化分割的协议,此协议可用手动分割来代表一组相关变化。实际上规模非常小的样本集对于一致的相关解释图像具有所有可能的感知[9]。文献[10]对于解决此问题中不均匀加权的图像像素对这种可变性设置在地面真像的统计方法。更确切地说,考虑一组相对应的手动分割分段图像其图像大小为N,设定Stest是手动标记集合和进行比较的分割指定的相关联区域标签与图像分割图Sgtk的像素位置xi,概率等级索引PRI的定义如式 (1)所示

其中针对pij估计值 (i和j像素具有相同的根据分割图的标签概率)的简单经验比例进行较好选择的方法,pij估计值计算如式 (2)所示

式中的δ符号是Kronecker函数。在此计算方法中,PRI计算方法是针对像素对进行简单等级索引计算得到的平均值[6]。因此,PRI计算方法将有利于得到可接受的分割图形,这种方法比较符合人类进行手动分割从而得到图像分割结果。图像分割也可能会有折中解决或一致共识,在水平层次详情和每个地面真像分割表现出的轮廓精度执行水平。在图1给出了融合图像实例,使用手动生成的图像分割,在细节水平上表现出细致变化。这个概率度量不会退化,所有的不良分割将提供低评价且不会出现例外。

图1 融合结果实例 (PRIF[K1=16|K2=10|K3=2])
1.2 正确分割产成Gibbs分布模型
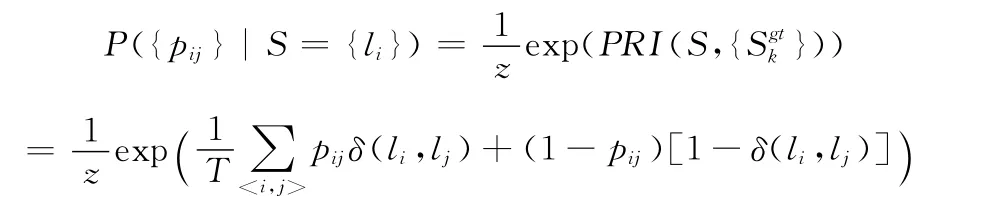
在文献 [6]中,{pij}(即在 {Sgtk}中进行计算每个像素对的成对经验概率定义)的集合定义正确分割小规模有吸引力的生成模型图像,简单表示为Gibbs分布模型。Gibbs分布模式可以生成正确的分割模式 (S={li}),这也可以当作是S的似然估计值。在这种方式中,基于PRI的含义可将后验概率表示为如下变化形式此式中的〈i,j〉是基于二阶派系或二进制派系的马尔可夫随机场 (MRF)模型定义的完整图形 (每个节点或像素点xi都连接到所有其它像素点图像)和T=N(N-1)是符合Boltzmann—Gibbs分布模型,这是两次小于等级索引中的归一化因子的温度因数。因为当i<j时,有两次以上的二进制派系比〈i,j〉对像素。Z是恒定分区函数,经过简化后表示为如式 (3)所示

其中,Z1=Z/exp(r)是恒定分区函数 (r参数只依赖数据因素),即表达为如下形式。
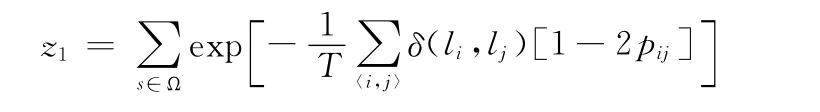
Ω是集中所有可能配置区域(S={li})且大小为N的像素分割而成的集合。因为类数量或者分割区域数目不是先验概率已知的情况,类数量之间并不同于区域数目N在此图像中的像素点位置。在此配置区域中,(1-2pij)可被看作潜在的空间变化二进制派系 (或成对相互作用区域)的等效非平稳马尔可夫随机场,其中被设定为一组代表地面真像分割情况下的正确分割生成模型。此外,针对S中的分割结果进行比较后可得 ({Sgtk}),可看作是实现与PRI生成模型,其极大似然估计是成比例的统计测量方法。S集合的估计值在此生成模型中最大似然估计可以得到的图像分割结果 (即融合结果),具有较高准确度以待融合的组分割
1.3 标签字段融合模型的图像分割
针对L集合的分割 {S1,S2,...,SL}子集,与大小为 N的相互关联的集合关系是紧密的 (即可以有效进行融合),以便能够获得最终可靠准确的分割图像结果。式 (3)中所提到的正确分割,可以在生成Gibbs分布模型中提供一个有效融合模型的分割图形,最大的PRI值或等价意义的基础Gibbs模型的最大似然估计 (maximum likelihood Estimator,MLE)表示如式 (3)所示。
在本框架中,{pij}集合的计算与经验比例估计 (具体见式 (2))的数据 {S1,S2,...,SL}。如果 {pij}具有估计值,极大似然估计融合分割映射则定义为最大似然分布具体如式 (4)所示

式中:UL——生成融合模式的可能性能量,应该尽量减少,以方便求解
对于相同或不同的像素标签,UL对约束集执行编码从而提供每个已被融合的L集合进行分隔。针对最小集UL执行生成的图像分割,还能够优化PRI具体标准。
1.4 贝叶斯融合模型的图像分割
图像分割问题是高斯法问题。它可以表达出多种不同可能值的类数量。要呈现此问题必须提出特定解决方案,在分割过程中定义部分必要的约束条件有利于减少过分割区域。从概率角度出发,可将这些正则约束看成是通过本地未知分割S={li}的具体实现。例如,随机字段内部的MRF框架或分析,编码所显示的现有能量的本地或全局先验概率可加入似然估计术语。
在本文提出的框架中,本文认为设置指定融合过程中的全局约束能量函数。此函数可在所得的图像分割结果图中限制区域数量。因此,本文将能量函数定义如式 (5)所示

式中:|R(S)|——在图像分割S中的区域数量 (设定连接属于同类型像素),H(·)——Heaviside函数,τ——融合模型内部参数的物理表示数目。以上这种存在约束限制区域数量。从概率来看,正规化约束对应到从τ开始的简单移动,随着最终分割显示区域数量呈现指数分布。
正规化解决方案对应的最大后验概率解决方案的融合模型的解决方案,即的最大后验分布定义是P(S|{pij}∝P(S)P({pij}|S)),因此可得式 (6)

在式 (6)中的β是正则化参数控制术语,UL表达进行组分割的准确度和融合后与UP关于可接受的最终分割作为估计的类型。以这种方式得到的相关标准,使用在本小节所得的融合模型可以看作是指定参数的最大等级估计值。
2 融合图像分割
由本文融合框架将被融合的初始分割简单映射,在应用程序中通过K—means聚类方法来对输入图像表示的不同色彩空间和不同数量的类进行应用。作为输入多维特征描述符,本文使用重新量化的颜色直方图的数值集合来与等距进行分级,从而通过估计周围像素来进行分类。在应用程序中,这个局部直方图同样进行重新量化,为每个图像的3种彩色通道运用Nb=q3b进行描述,计算重叠平方围绕来进行分类像素尺寸 (Nw=7)和固定邻域。
算法1:每个像素的Bin描述符估计算法:
参数:
(1)Nx:在Nw×Nw邻居区域设置以x为像素中心的位置x;
(2)h[]:Bin描述符,Nb实数数组 (h[0],h[1],...,h[Nb-1]);
(3).:取整数部分。
针对每个像素点x∈Nx,具有颜色值Rx,Gx,Bx,执行循环体:
(1)k←q2q·Rx/256 +q· q·Gx/256 + q·Bx/256 ;
(2)h[k]←h[k]+1/N2w;
(3)直到遍历所有像素点为止。
在这个简单模型中,纹理基元 (即重复字符或元素中有纹理的图像)在本文中其特征在于由更精确的混合颜色通过重新量化的本地颜色直方图的数值。这种模式是种简化计算模式,可以明显减少实际数据量,同时噪声和当地图像转换效率可证明相关跟踪应用。
最后,(q3b-bin)中的描述符可分为不同类型的簇,对应每个类的图像,通过经典的K—means算法中的L1范数(也称为Manhattan距离)。最后合并步骤中加入每个分割结果图,由定影每个小区域 (即:小区域大小为不超过200个像素)与该区域的共享最长边界。
每个分割结果图可通过执行时间来保持简单分割模式,根据K和q,未优化的C++代码执行时间在0.25秒至2秒之间。
这种简单的分割策略中的输入图像为K类进行不同的色彩空间 (它可被看作是不同图像通道提供的各种传感器或捕捉器),并为不同类型的K值和不同的qb值提供具体依据,qb值是不同值的重新量化颜色直方图的数量。
每种颜色空间都有一种属性,它可以使最终的融合过程结果更加可信。
基于RGB三原色理论的加色系统属于非线性视觉感知。这种色彩空间是用于跟踪的最佳应用程序。由于HSV具有优秀的去除相关属性的识别能力和传输效率,YIQ系统的优点是利用人类颜色响应特性。XYZ具有心理视觉特性,它是具有非线性分量和线性分量混合色彩的优点。LAB颜色系统则接近人类视觉,L分量密切匹配人类感知亮度。LUV组件提供欧氏颜色空间来产生听觉均匀的间距颜色近似Riemannian空间 (在此空间内的两点之间的欧氏距离可表示更多或更少感知区别)。I1I2I3是近似Karhunen Loeve转换的RGB空间。它创建颜色通道是正交性完全相关。因此,这个颜色系统具有的属性,以实现最佳的能量压缩并呈现出亮点和光照强度不变。H1H2H3是唯一的颜色空间,它也是唯一具有通道差异的。最后,针对TSL彩色空间使用高斯模型是行之有效的皮肤分割和检测方法。
这些有待融合的初始分割可以提供由不同分割模型或不同分割结果来提供的不同随机分割模型。不同结果与不同初始化都是由不同通道提供的,不同图像中相同确定性分割器或传感器,最后提供不同评价指标的K—Means聚类得到的输出结果。
3 图像分割实验结果
3.1 实验环境说明
在本文实验中,已经考虑本文融合方法中平方窗口大小主要用来计算初始分割的局部直方图的简单分割模型,在第2节种得到初始分割大小为Nw=7×7。
实验表明,本文融合模型是行之有效的。如果要融合的初始分割是多样化的,同时为了方便实验具有普适性,作者考虑进行60种融合分割。
(1)10种不同的颜色空间 (NS=10),具体分别是RGB,HSV,YIQ,XYZ,LAB,LUV,I1I2I3,H1H2H3,YCbCr,TSL。
(2)3个不同数值的类,分别为K1,K2和K3。
(3)两种不同数目的量化颜色直方图,即:Nb=53与Nb=43情况。
3.2 性能比较及对策
在本文实验中,首先测试本文分割算法在Berkeley分割数据库中的结果。Berkeley数据库由300幅大小为481×321的彩色图像构成,数据库分为200幅训练图像集合和100幅测试图像集合。针对每幅彩色图像,人类观察者提供的一组基准分割结果是有效的,将被用于量化进行图像分割算法可靠性。为了确保评价完整性,本算法的内部参数 (K1,K2,K3,β、τ)在参数空间上和在有效范围内的参数值 (即:K1,K2,K3∈ [2-20][步长为2],β∈ [0-4000][步长为1000],τ∈ [5-20][步长为5])。该算法是通过在标记使用独立测试集的最佳训练参数,我们把本文算法与5种无监督公开算法进行比较,称为PRIF[K1|K2|K3][β,τ],PRIF 、K1、K2、K3、β和τ 是它的内部参数。对于每个算法来说,内部参数设置为最佳值和本文建议数值。这些算法的均值漂移 (hs=13,hr=19),所有彩色图像归一化到具有第320个像素的最长边为止。然后,超级采样分割结果与原来分辨率 (481×321)的估计性能度量以获得分割结果图像。
基于PRI性能比较方法,即:PRI=0.80意思是平均80%的像素对所在标签能够进行正确分类并得到图像分割结果。F—Measure方法能够推论出的图像分割的准确度/反馈值,表示两个图像分割区域边界之间的协议。F—Measure方法目前已广泛应用于计算机视觉和边缘检测领域。准确度测量Measure(P)定义为真实边界的检测部分;F—Measure数值低表示有明显的过分割现象,或大量边界像素具有较差的本地化趋势。反馈值Recall(R)的测量结果可提供真实边界检测,反馈值较低时通常表示根据分割结果表示未能获得显著的图像结构。因此,在精确量化的噪声检测器输出结果中,而回收量量化的检测到的地面真像。边界检测器性能可提供由精确反馈的平面中的像素点的二进制输出表示。如果输出的是软边界图像,参数的精确反馈曲线则表示主要参数各不相同的边界探测器中没有噪声和真实度之间的折中解决地面真像。查准率和查全率可以结合质量统计措施,F—Measure方法 (F=2PR/(P+R))定义为它们的调和平均值能够结合精确度和反馈值作为衡量性能的相关标准。精确反馈可用曲线上的最大F—Measure数值性能的探测器的图像作为简要统计数据。
3.3 测试结果
在PRI方法中,本文观察到所讨论的融合策略提供了有效结果 (PRI=0.80意思是平均80%的像素对所在标签能够进行正确分类并得到图像分割结果),在相对较低的方差Berkeley图像数据库的图像设置。图2算法PRIF[K1=18|K2=10|K3=2]是针对 Berkeley图像数据集中的300张图像,在表示出的分布PRI方法。

图2 Berkeley数据库中PRI性能指标分布
在F—Measure方法中,可以发现所获图像分割与较低的F—Measure值相比现有的最好的边界检测算法的最高分数是F=0.70@(0.71,0.68)。本文算法也给出了比较大部分边界探测器基准的一组封闭曲线,这组曲线表示为“硬”边界。基于此原因,本文算法与最佳边界检测算法[4]中提出的确定图像分割图 (即封闭曲线)来进行比较,F—Measure值则是F =0.67@(0.69,0.66)。
因为基础算法 (计算F—Measure)将会在不要封闭轮廓的基础上寻找最优阈值,“软”输出这项措施更为适合本文算法。本文分割结果和地面真像所提供的Berkeley数据库的对比结果表明,本文算法往往有过分割现象,从而导致噪声信号 (即假轮廓)在最终分割结果中出现。为了证明此情况,并客观比较的本文分割方法与最佳边界探测器(探测器一般提供 “软”输出,其阈值操作不能保证是封闭轮廓),本文测试使用的是最终 “硬”边界表示转换到“软”版本,只需更换由数值梯度幅值的每一个检测到的边界像素的Nb-bin描述符 (即:重新在基于初始颜色图像的小型平方大小窗口上量化本地计算颜色直方图,请参阅算法1)。通过计算每个位于行与列的像素点 (检测为分界点),下面计算简单距离的公式为
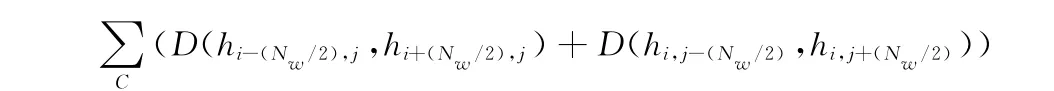
求和运算在10个不同色彩空间种,D(hi-d,j,hi+d,j)是Manhattan距离 (L1范数)之间的矢量,计算一个平方Nw-size的窗口hi-d,j和hi+d,j分别在中心位置 (i-d,j)和(i+d,j)(参见算法1)。根据结果显示得分最高的FMeasure值为F=0.63@(0.62,0.63)。
3.4 结果讨论
通过图4可见当Ns(针对分割数进行融合)较高时,PRI测量性能更好。同样可在F—Measure方法中进行测量。本实验表明本文融合过程具有不断完善的算法有效性。如果需要进一步改进,可以增加与Nb=33进行融合,或使用不同的特征描述符或不同的相似性度量直方图之间的通过下列方式获得的聚类结果,来获得图像分割映射到组分割的描述符。
例如分割Berkeley数据库图像区域的大小区域数量和分布情况,由本文方法的图像分割结果执行统计,算法PRIF[K1=18|K2=10|K3=2]的运行结果在图5和图6中描述。
为了进一步验证本文融合过程中,本文尝试了几种均值漂移的图像分割时间间隔内分别随机融合hs与hr间隔在[2,...,15]和 [20,...,40]之间。本文融合过程中显著提高性能方法,在单一图像分割比较得到:PRI=0.7905。
最后测试本文融合算法针对所述组输入手工标记的地面真像进行分割相关的给定的Berkeley图像 (参见图3分割结果)。为了使这方面的分割效果更为详细,本文选择的是自然图像,它表现出高度变化分割的整体存在。将所得融合图像 (参见图3)的显著区域平均数目,相对的组地面真像可以比喻成具有相同数量图像分割的手动生成的输入信息。本文融合模型添加了正面Gibbs能量模型,也可以计算每个地面真像进行分割的准确度,输入地面真像的集合;在与反面Gibbs能量成正比的PRand度量中,每个输入分割向所得的融合地图。然后,此信息可被有效地利用,删除异常值或加权的信心,每个输入分割均在PRI Sense中。




图3 Berkeley图像具体分割实例
4 结束语
本文提出在细分策略基础上的马尔可夫贝叶斯融合过程。目标是把几个快速估计的分割模型进行融合以求达到更可靠、更准确的图像分割结果。这种融合模型是实现惩罚的最大PRI意义上有准确意义。与普通的语言到各种数字图像和计算机视觉应用程序相比,融合的图像分割可以简单完美地实现这种融合框架。
本文认为此种融合模型较容易使贝叶斯融合模型并行化,为图像分割的细分模型中存在困难图像分割问题提供解决方案。
[1] Mignotte M.Segmentation by fusion of histogram—based k—means clusters in different color spaces [J].IEEE Transactions on Image Processing,2008,17 (5):780—787.
[2]Ma Y,Derksen H,Hong W,et al.Segmentation of multivariate mixed data via lossy coding and compression [J].IEEE Transactions on Pattern Analysis Machine Intelligence,2007,29 (9):1546—1562.
[3]Reed S,Ruiz I R,Capus C,et al.The fusion of large scale classified side—scan sonar image mosaics [J].IEEE Transactions on Pattern Analysis Machine Intelligence,2006,15(7):2049—2060.
[4]Jodoin P M,Mignotte M,Rosenberger C.Segmentation framework based on label field fusion [J].IEEE Transactions on Image Processing,2007,16 (10):2535—2550.
[5]Kato Z.A Markov random field image segmentation model for color textured images[J].Image Vision Computation,2006,24 (10):1103—1114.
[6]Yang A Y,Wright J,Sastry S,et al.Unsupervised segmen—tation of natural images via lossy data compression [J].Computational Vision Image Understanding,2008,110 (2):212—225.
[7]Unnikrishnan R,Pantofaru C,Hebert M.Toward objective evaluation of image segmentation algorithms [J].IEEE Transactions on Pattern Analysis Machine Intelligence,2007,29 (6):929—944.
[8]Ilea D E,Whelan P F.CTEX—an adaptive unsupervised segmentation algorithm on color—texture coherence [J].IEEE Transactions on Image Processing,2008,17 (10):1926—1939.
[9]Martin D,Fowlkes C.The berkeley segmentation database and benchmark [M/OL].University California,Berkeley,2010.[2010—05—06].http//www.cs.berkeley.edu/projects/vision/grouping/segbench/.
[10]Maire M,Arbelaez P,Fowlkes C,et al.Using contours to detect and localize junctions in natural images [C]//Proc of IEEE Conference Computation Vision Pattern Recognition,2008:1—8.
[11]ZHANG Hengwei, YANG Youlong, ZHU Yuanyuan.Multi—step prediction of frequency—hopping sequences based on Bayesian networks [J].Application Research of Computers,2012,29 (1):237—240 (in Chinese).[张恒伟,杨有龙,朱原媛.基于贝叶斯网络的跳频序列多步预测 [J].计算机应用研究,2012,29 (1):237—240.]
[12]QIAN Zhengming,GUAN Rui.Application of reliability model about computer business information system based on Bayesian network [J].Application Research of Computers,2012,29 (12):4651—4653 (in Chinese). [钱争鸣,管睿.基于贝叶斯网络的计算机经济信息系统可靠性模型及其应用[J].计算机应用研究,2012,29 (12):4651—4653.]
