立足教材 突出核心 引导教学——大连市2012年中考数学试题特点及教学启示

王 冰

(大连教育学院 初中教师教育中心，辽宁 大连 116021)

立足教材 突出核心 引导教学
——大连市2012年中考数学试题特点及教学启示

王 冰*

(大连教育学院 初中教师教育中心，辽宁 大连 116021)

通过分析大连市2012年中考数学试题的特点，说明初中数学教学应关注教材、用好教材，把握核心，重视思想。

2012年中考;数学试题;突出特点;教学启示

大连市中考数学试卷具有毕业与选拔两种功能。2012年中考数学试卷的命制继续坚持“四个有利于”的指导思想，即有利于引导和促进数学教学全面落实《全日制义务教育数学课程标准(实验稿)》所设立的课程目标;有利于引导和改善学生的数学学习方式，提高学生数学学习的效率;有利于减轻学生过重的学业负担，促进学生素质提高;有利于高中阶段学校综合、有效地评价学生的数学学习状况。整个试卷不仅重视对学生学习数学知识与技能的评价，而且重视对学生在数学思考能力和解决问题能力等方面发展状况的评价。试卷面向全体学生，力求公正、客观、全面、准确地评价学生通过初中教育阶段的数学学习所获得的发展状况。

一、试题的突出特点

1．立足教材

教材(教科书)是学生学习的主要素材之一，为了有效引导师生重视教材、用好教材，改变当前存在的忽视教材、脱离教材的状况，大连市2012年中考数学试题绝大多数都源于教材，很多试题都能在教材题中找到“影子”。

试卷中的第4题原型为教科书八年级下册第140页的例1。

第4题:甲、乙两班分别有10名选手参加学校健美操比赛，两班参赛选手身高的方差分别为=1．5=2．5，则下列说法正确的是()

A．甲班选手比乙班选手身高整齐

B．乙班选手比甲班选手身高整齐

C．甲、乙两班选手身高一样整齐

D．无法确定哪班选手身高更整齐

教材原题:在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高(单位:cm)分别是:

甲团:163 164 164 165 165 166 166 167

乙团:163 165 165 166 166 167 168 168

哪个芭蕾舞团女演员的身高更整齐?

试卷中的第13题原型为教科书九年级上册第142页的练习1。

第13题:下表记录了一名球员在罚球线上投篮的结果:

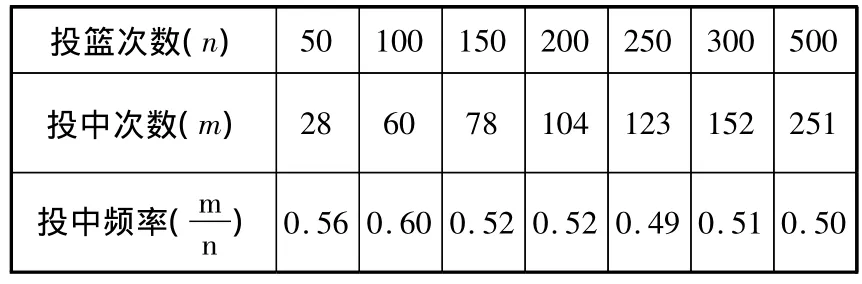
投篮次数(n) 50 100 150 200 250 300 500投中次数(m) 28 60 78 104 123 152 251投中频率(m n )0．56 0．60 0．52 0．52 0．49 0．51 0．50

那么，这名球员投篮一次，投中的概率约是＿＿(精确到 0．1)．

教材原题:下表记录了一名球员在罚球线上投篮的结果:

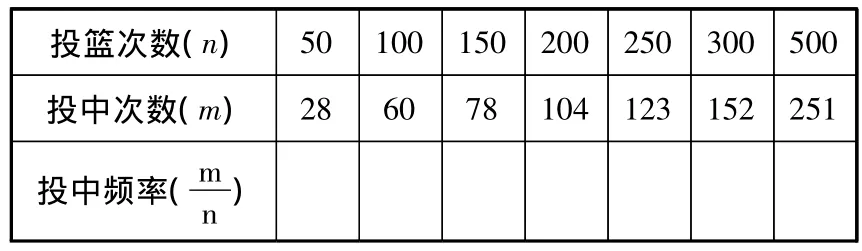
投篮次数(n) 50 100 150 200 250 300 500投中次数(m) 28 60 78 104 123 152 251投中频率(m n )

(1)计算表中的投中频率(精确到0．01);

(2)这名球员投篮一次，投中的概率约是多少(精确到 0．1)?

试卷中的第23题原型为教科书九年级上册第103页的第14题。

第23题:如图3，AB是⊙O的直径，点C在⊙O上，∠CAB的平分线交⊙O于点D，过点D作AC的垂线交AC的延长线于点E，连接BC交AD于点F．

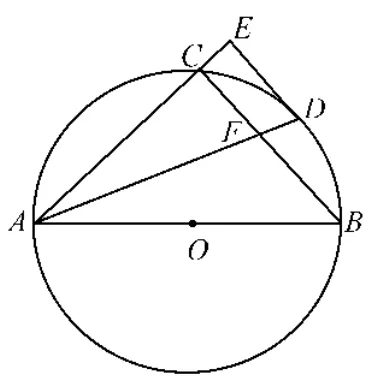
图3

(1)猜想ED与⊙O的位置关系，并证明你的猜想;

(2)若 AB=6，AD=5，求 AF 的长．

教材原题:如图4，AB是⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为 D，求证 AC平分∠DAB．

图4

2．突出核心

试卷在注重考查初中阶段数学基础知识和基本技能、保证考查的覆盖面的同时，更加关注数学核心内容，突出考查了核心的知识点、重要的数学思想方法以及对数学本质的理解。

第 24题:如图 5，△ABC 中，∠C=90°，AC=8cm，BC=6cm，点 P、Q 同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动，当点Q到达点B时，点 P、Q同时停止运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ'R．设点Q的运动时间为t(s)，△PQ'R与△PAR重叠部分的面积为S(cm2)．

(1)t为何值时，点Q'恰好落在AB上?

(2)求S与t的函数关系式，并写出t的取值范围;

图5

本题以初中数学的核心知识——直角三角形、平移、轴对称、相似、函数、一元二次方程等为载体，将代数与几何有机结合，综合考查了学生运用数形结合思想、函数与方程思想、分类思想、转化思想解决具体问题的能力，较好地体现了能力立意。

第25题:如图6，梯形ABCD中，AD∥BC，∠ABC=2∠BCD=2α，点 E 在 AD上，点 F在 DC上，且∠BEF=∠A．

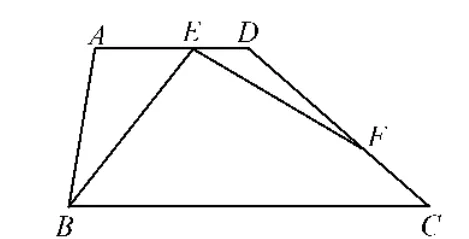
图6

(1)∠BEF=＿＿(用含 α的代数式表示);

(2)当AB=AD时，猜想线段EB、EF的数量关系，并证明你的猜想;

(3)当AB≠AD时，将“点E在AD上”改为“点E在 AD的延长线上，且 AE＞AB，AB=mDE，AD=nDE”，其他条件不变(如图7)，求的值(用含m、n的代数式表示)．

本题以初中几何的核心知识——平行线、全等三角形、相似三角形、几何变换等为载体，综合考查了学生的空间观念、推理能力和创新意

识。解答此题，学生要经历观察、比较、猜想、证明等数学活动过程，要从特殊到一般探究两条线段的数量关系，此过程较好地考查了新课标中重点强调的“四基”，即基础知识、基本技能、基本思想和基本活动经验。特别是对三个基本思想中的抽象思想和推理思想以及对数学活动经验——实践的经验和思维的经验进行了比较充分的考查。

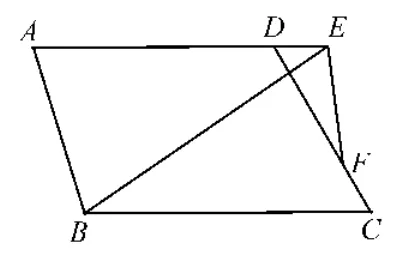
图7

第 26题:如图8，抛物线 y=ax2+bx+c经过A(－，0)、B(3，0)、C(0，3)三点，线段BC与抛物线的对称轴l相交于点 D．设抛物线的顶点为 P，连接PA、AD、DP，线段AD与 y轴相交于点E．

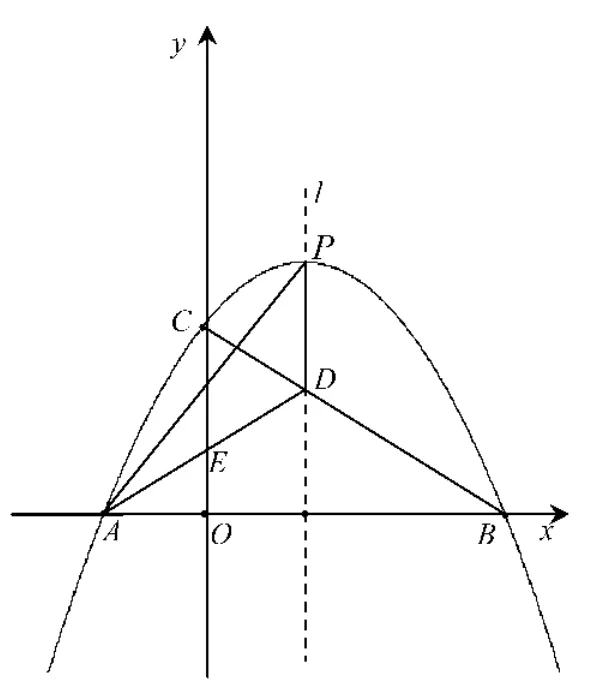
图8

(1)求该抛物线的解析式;

(2)在平面直角坐标系中是否存在点Q，使以点Q、C、D为顶点的三角形与△ADP全等?若存在，求出点Q的坐标，若不存在，说明理由;

(3)将∠CED绕点E顺时针旋转，边EC旋转后与线段BC相交于点M，边ED旋转后与对称轴l相交于点 N，连接 PM、DN，若 PM=2DN，求点 N的坐标(直接写出结果)．

本题以初中数学的核心知识——二次函数、等边三角形、菱形、三角形全等、三角形旋转、菱形的轴对称性等为载体，综合考查了学生对初中阶段的数与代数、图形与几何两个领域中的核心知识点的掌握程度，以及学生运用数形结合思想、分类讨论思想、几何变换思想、方程思想、转化思想等解决问题的能力，较好地体现了试题的选拔功能。

二、教学启示

1．重视教材，用好教材

数学教材是课程专家根据《数学课程标准》规定的教学目标、教学内容、教学要求以及学生的年龄特征和认知水平，按照数学学科的科学性、系统性、严密性、实用性、教育性以及教学法的要求，为在校学生编写的数学学习的专门用书。它是教师备课、上课、布置作业和检查学生学业成绩的基本材料，是学生自主学习的基本材料，是学校师生教与学的主要依据。它是经全国中小学教材审定委员会严格审核通过的，具有很强的指导性和权威性。但是，在教学中经常看到这样一种现象:教师忽视对教材内容中知识的本质特征与内在联系的深入钻研，在课堂上只用很少的时间讲授教科书中的主要知识点，而将大量的时间用于做题，课后布置大量作业让学生反复做，本意是想弥补学生知识理解的不足，结果事倍功半，学生负担过重，苦不堪言。为了改变这种忽视教材、脱离教材的现状，减轻学生过重的学习负担，大连市2012年中考数学试题加大了对教材例习题的改编力度，以期引导教师重视教材，用好教材，达到事半功倍的教学效果。教师只有深入挖掘教材，透彻理解教材，明确教材的编写意图，才能做到基于教材、超越教材，创造性地设计出符合学生学习规律、体现数学学科特点的教学过程，让学生在经历知识发生、发展的过程中学习数学知识，感悟数学思想，积累数学活动经验，逐渐由学会数学向会学数学转变。只有这样，学生在面临新的数学情境、新的数学问题时，才能从容淡定、应对自如。

2．把握核心，重视思想

数学核心内容、思想方法是初中数学学科体系的灵魂。在初中阶段，数学学科涉及的知识点汇成了数学结构系统的两条“河流”。一条是由具体的知识点构成的易于被发现的“明河流”，数学核心内容是“明河流”的主要交汇点，它是构成初中数学学科的“骨架”;另一条是由数学思想方法构成的具有潜在价值的“暗河流”，它是构成初中数学学科的“血脉”和灵魂。有了数学思想作灵魂，各种具体的数学知识点才不再孤立、零散。因为数学思想能将“游离”状态的知识点凝结成优化的知识结构，有了它，数学概念和命题才能活起来，做到相互紧扣，相互支持，组成一个有机整体。教师在教学中只有抓住数学核心内容、思想方法这一主线，才能高屋建瓴，取得更大的教学效益。学生只有真正把握了数学核心内容和重要的数学思想方法，才能跳出题海，走出就题论题的小路，走上以题论“法”、以题论“道”的大道。这里的“法”就是以核心内容为载体的解决数学问题的基本方法，这里的“道”就是数学思想方法。

［责任编辑:阅力］

Standing on Textbooks，Highlighting Core and Guiding Teaching——Features of Math Test Questions of Dalian 2012 Senior High School Entrance Exam ination and Teaching Enlightenment

WANG Bing
(Center of Junior High School Teacher Education，Dalian Education University，Dalian 116021，China)

Based on the analysis ofmath test characteristics of Dalian 2012 senior high school entrance examination，the paper expounds that teachers should pay attention to textbooks，make best use of textbooks，master the core and attach importance to ideas in juniormiddle schoolmathematics teaching．

2012 senior high school entrance examination;math test questions;highlight features;teaching enlightenment

G632．3

A

1008-388X(2013)01-0055-03*

2013-01-04

王冰(1964-)，女，辽宁鞍山人，中学高级教师。