基于改进马氏距离的模糊C聚类研究

赵小强，李雄伟

(兰州理工大学 电气工程与信息工程学院，甘肃 兰州，730050)

基于改进马氏距离的模糊C聚类研究

赵小强，李雄伟

(兰州理工大学 电气工程与信息工程学院，甘肃 兰州，730050)

提出一种基于改进马氏距离的模糊C聚类算法，先通过对数据集进行加权，然后对数据的马氏距离进行协方差处理。研究结果表明：该方法可以对高相关属性的数据集进行有效分类，能降低分错率，该方法具有可行性和有效性。

模糊C均值；高相关属性；马氏距离；协方差矩阵

模糊聚类算法是基于模糊论的聚类算法研究，其算法迭代速度比一般的聚类算法快，近年来，广泛应用于图像处理、机器学习、模式识别和数据挖掘等方面，逐渐成为一个研究热点。在诸多的聚类算法中，模糊C均值(FCM)算法的理论比较成熟，应用范围相对广泛，它是以硬聚类(HCM)为基础经过进一步推导而得出的[1−2]。为了使FCM算法具有一般性，Bezdek[3]引进参数m，使 FCM的目标函数推广到了无限族，讨论了 FCM 的收敛问题，并证明了其最终收敛到一个极值，从而演变成一般情况下的 FCM 算法。近年来，FCM算法已经成为大家深入研究的重点领域，许多学者针对实际情况遇到的不同问题，提出了各种改进的聚类算法，如李洁等[4]针对样本向量中各维特征对模式分类的不同影响，提出基于特征加权的模糊聚类新算法；Xing等[5]为了解决样本分布不均的问题，提出了一种基于专家模型的自适应FCM；李翠霞等[6]提出的一种模糊聚类算法归类的研究是针对噪声数据敏感和鲁棒性较差问题。但是传统的 FCM 算法是主要解决空间中数据点与点之间的聚类问题，它只适用于凸型数据，而不适用于非凸型数据。Schikuta等[7]提出 Bang聚类系统在处理数据结构方面有所提高，但是当数据的维度增加时，其效果不理想。FCM聚类中的目标函数采用马氏距离，因为马氏距离可以调整数据点在空间中的分布，使相关性强的数据点集中在一起，可以比较好地解决欧式距离属性相关的问题。然而分布点的集中又会带来数据高斯分布的问题，使错分率的概率大大增加。而且，在马氏距离计算中如何解决奇异性问题是个难点。因此，本文作者通过改进协方差矩阵的估计来提高马氏距离聚类分析效率，并将改进的马氏距离的FCM算法应用于UCI数据集聚类中，实验验证了该方法的可行性和有效性。

1 模糊C均值聚类方法

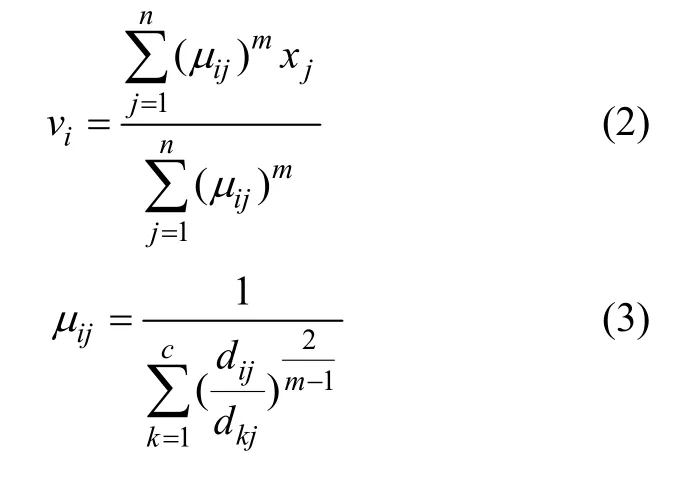
2 基于改进马氏距离的模糊 C均值聚类

2.1 特征空间的马氏距离

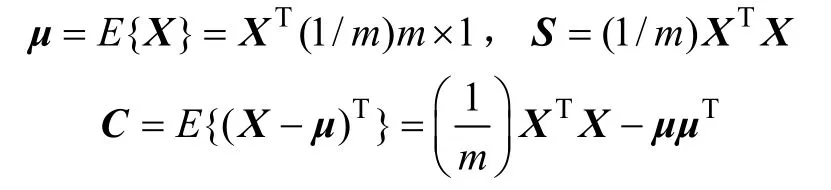
式中，(1/m)m×1代表元素均为1/m的m维列矢量。样本xi到样本总体X的马氏距离为：

若协方差矩阵Σi是奇异的，则马氏距离无解。依据矩阵的相关理论，对于任意一个秩为r的实对称半正定矩阵可按以下方式分解，Σi为实对称半正定矩阵，设Σi的秩为r，则Σi可以分解为ΣTi=AGA，G为r×r的对角阵，它由Σi的非0特征值构成，G是非奇异的。A为r×m矩阵，由G中特征值所对应的特征向量构成，且ATA为r×r的单位阵。分解后，便可根据G的逆来求Σi的伪逆：

2.2 基于改进马氏距离的模糊聚类

在所有的测度计量中，往往通过对属性的描述来体现两者之间的相似性，马氏距离就是一种测量相似度的方法。一般情况下，将重要位置的属性赋予相对比较高的权重，从而突出属性相似度对聚类效果的影响。在样本空间中，样本i的每个特征p在类c上的马氏距离公式为：

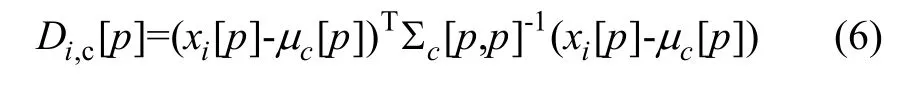
基于式(6)，本文提出一种改进马氏距离模糊C均值聚类。计算马氏距离，首先要根据已知的样本数估计协方差矩阵。此时，协方差矩阵的估计值必然与样本个体的类别有关系，而类别的判定又取决于聚类分析，那么这就会陷入一个不断循环的困境。因此，对于马氏距离中的协方差矩阵通常用全体数据的样本协方差矩阵来代替。因为这种做法忽略了类别对取样结果的影响，所以需要将变量的权重和样本的类别对协方差矩阵估计的影响考虑进去，从而对协方差矩阵进行从新估计。

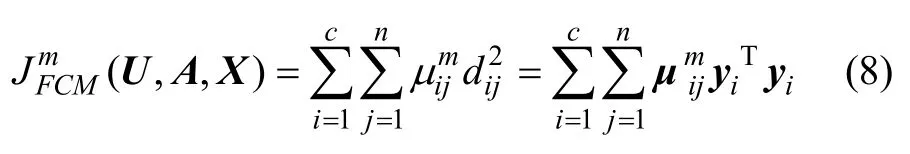
M-FCM算法步骤如下：

步骤1 确定类数c，并且设定各个变量的权重ωi，i=1，…，p；

步骤 2 进行初始化处理：给定聚类类别数c，2≤c≤n，n是数据数，设定迭代停止阈值ε，初始化聚类中心矩阵 A(0)，设置迭代计数器b=0，用式(3)计算或更新隶属度矩阵U(b)，用式(2)更新聚类中心矩阵A(b+1)，如果||A(b)−A(b+1)||＜ε，则算法停止并输出隶属度矩阵U，和聚类中心A；

步骤5 对数据进行加权马氏化处理, 得到新的数据集；

步骤6 对新数据集进行欧氏距离聚类分析；

步骤7 重复步骤3～6，直到聚类结果收敛为止。

3 实验验证

从UCI中选取4个数据集对算法进行验证。首先将各数据集使用式(7)进行加权马氏距离化处理，然后用FCM算法。算法的测试平台为WindowsXP，选择CPU P4 2.66 GHz，内存256 Mb的PC机为测试环境，程序的编写用Matlab语句。

3.1 实验数据与结果

在UCI数据库中提取的4个数据集分别为：Iris(鸢尾植物数据库)，Glass(玻璃识别数据库)，Wine(葡萄酒数据库)和Pima(皮马印第安人糖尿病数据库)。4个数据集基本特征见表1。表2所示为传统FCM与新算法的聚类结果的比较，其中M-FCM算法为基于改进马氏距离的FCM算法。

IRIS数据是鸢尾植物数据库，最初是用来它测量地理变化的，后来应用在了统计学中。它主要分布在3种不同类别的鸢尾花，即山鸢尾、变色鸢尾和维吉尼亚鸢尾，每一类鸢尾花各占50个样本。每一个样本中都有花萼的长度，花萼的宽度，花瓣的长度和花瓣的宽度4个特征作为属性。其中山鸢尾与其他2类之间能很好的分离，它是线性的。而变色鸢尾和维吉尼亚鸢尾之间存在交叉重叠的部分，是非线性的。

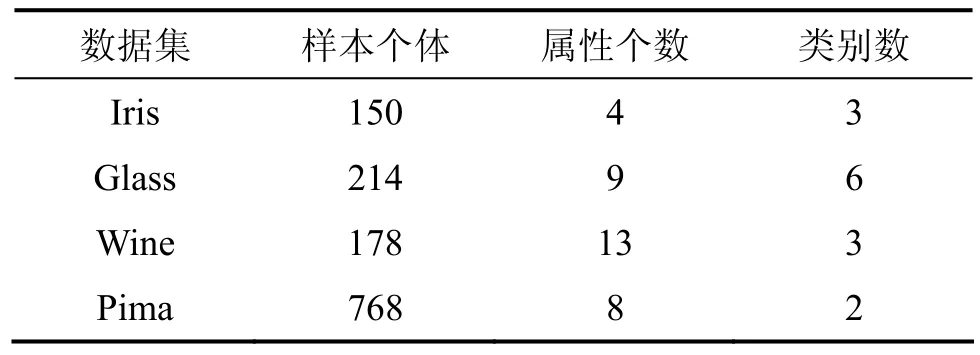
表1 数据集的特征描述Table 1 Characteristic description of data set

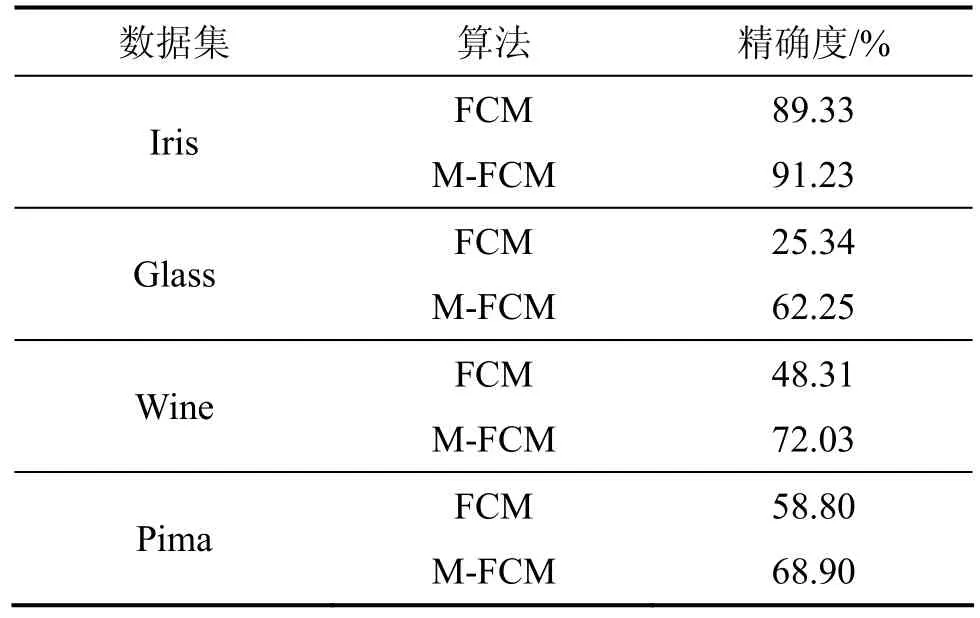
表2 不同算法聚类结果的比较Table 2 Comparison of different clustering results

Glass数据集是一种玻璃识别数据库，主要是应用于犯罪现场。在案情侦破中，通过识别现场留下的玻璃碎片属性来作为犯罪分子的犯罪证据。主要以折射率、钠、镁、铝、硅、钾、钙、钡、铁等9个参数作为特征，6个类属性，它们分别为70个浮点法处理大厦的窗户、76个非浮点法处理大厦的窗户、17个浮点法处理车窗、0个非浮点法处理车窗、13个集装箱、9个餐具、29个前大灯共同构成214个样本个体。

Wine数据集为生长在 Italy 同一区域不同葡萄园产出的3种葡萄酒，并把它们的化学分析结果的作为样本，以酒精、灰、苹果酸、灰的碱度、镁、总酚类、黄酮、非黄酮酚类、原花色素、颜色强度、OD280/OD315 稀释的葡萄酒、脯氨酸等13个参数作为数据的特征，一般可以分为3个类别，第1类有59个样本点，第2类有71个样本点，第3类有48个样本点，一共有178个样本,由上面的13个特征和178个样本点一起构成了178 ×13 维矩阵。

Pima数据集是皮马印第安人糖尿病数据库，主要是指在年满 21岁的女性皮马印第安人的遗传病例参数、包括怀孕次数、 2 h血浆葡萄糖浓度在口服葡萄糖耐量试验、舒张压、三头肌皮褶厚度(mm)、 2 h血清胰岛素、身体质量指数、糖尿病血统函数、年龄、变量(0或1)等8个属性，其中类值1被解释为“检测呈阳性糖尿病其值为268，类值0被解释为“检测呈阴性糖尿病”，其值为500。

3.2 实验结果分析

M-FCM算法的聚类效果比FCM算法的更优，对不同的数据类型，算法精确度的提高程度有很大的差异性。当数据集属性相关性的程度增大时，该算法的精确度普遍提高。Glass数据集精确度提高非常明显，Wine和Pima数据集的精确度幅度次之；而且M-FCM算法在迭代过程中均收敛。这说明M-FCM算法的适用不仅跟数据集的属性相关度有关，而且其结果比FCM的更好。

4 结论

(1) 提出了一种数据加权马氏距离的 FCM(即M-FCM)算法，将马氏距离模糊C均值聚类算法分成2个步骤，首先是对数据加权重之后进行马氏化处理，然后在采用欧氏距离的聚类过程，反复进行迭代直到结果收敛为止。

(2) 采用改进之后的马氏距离对Iris，Glass，Wine和Pima数据集进行仿真，聚类效果有提高显著。

(3) 虽然马氏距离在进行分类时有较好的性质，但是在处理协方差矩阵的估计问题时，方法比较多，如何选择一种最有效的方式是以后关注的问题。

[1] Duda R O, Hart P E. Pattern classification and scene analysis[M].New York: John Wiley &Sons, 1973: 230−235.

[2] Duma J C. Well-separated clusters and the optimal fuzzy partitious[J]. J Cybernet, 1974, 4(1): 95−104.

[3] Bezdek J C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press, 1981: 193−203.

[4] 李洁, 高新波, 焦李成. 基于特征加权的模糊聚类新算法[J].电子学报, 2006, 34(1): 89−92.

LI Jie, GAO Xinbo, JIAO Licheng. A new feature weighted fuzzy clustering algorithm[J]. Acta Electronica Sinica, 2006,34(1): 89−92.

[5] XING HongJie, HUA Baogang. An adaptive fuzzy C-mean clustering-based mixture of experts model for unlabeled data classification[J]. Nero Computing, 2008, 71: 1008−1021.

[6] 李翠霞, 于剑. 一种模糊聚类算法归类的研究[J]. 北京交通大学学报, 2005, 29(2): 17−21.

LI Cuixia, YU Jian. Study on the classification of a kind of fuzzy clustering algorithm[J]. Journal of Beijing Jiao Tong University,2005, 29(2): 17−21.

[7] Schikuta E, Erhart M. The BANG-clustering system: Grid-bused data analysis[C]//Lecture Notes in Computer Science Band 1280.London: Springer, 1997: 513−524.

(编辑 赵俊)

A fuzzy C-means clustering algorithm based on improved Mahalanobis distance

ZHAO Xiaoqiang, LI Xiongwei

(College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

A fuzzy C-means clustering algorithm based improved Mahalanobis distance was proposed. The datasets were weighted and then covariances of Mahalanobis distance were calculated. The results show that the method can effectively cluster for datesets of high correlation and reduce error probability. The method has effectiveness and feasibility.

fuzzy C-mean clustering; high correlation property; Mahalanobis distance; covariance matrix

TP273

A

1672−7207(2013)S2−0195−04

2013−03−01；

2013−05−02

甘肃省高校基本科研业务费项目省财政厅项目(1203ZTC061)；甘肃省制造业信息化工程技术研究中心开放基金资助项目(1112RJZA028)

赵小强(1969−)，男，陕西岐山人，博士，教授，从事生产调度、数据挖掘与故障诊断研究；E-mail：xqzhao2008@gmail.com