大尺寸混凝土箱梁日照温度场的实测与仿真分析
2013-02-07顾斌陈志坚陈欣迪
顾斌,陈志坚,陈欣迪
(1. 河海大学 土木与交通学院,江苏 南京,210098;2. 河海大学 地球科学与工程学院,江苏 南京,210098;3. 河海大学 港口海岸与近海工程学院,江苏 南京,210098)
大尺寸混凝土箱梁日照温度场的实测与仿真分析
顾斌1,陈志坚2,陈欣迪3
(1. 河海大学 土木与交通学院,江苏 南京,210098;2. 河海大学 地球科学与工程学院,江苏 南京,210098;3. 河海大学 港口海岸与近海工程学院,江苏 南京,210098)
基于对苏通大桥辅助航道桥运营期温度数据的分析以及对不同尺寸箱梁的温度场的仿真计算,研究大尺寸箱梁温度场的分布特点及其影响,提出腹板温度梯度和底板温度梯度的修正方法。研究结果表明:大尺寸混凝土箱梁竖向温度分布特点为腹板温度整体高于梗腋部位温度,而梗腋部位的温度又整体高于底板温度;计算大尺寸混凝土箱梁的温度效应时,由腹板温度和底板温度引起的竖向挠度曲率误差最高可达33.3%。腹板沿壁厚方向最大温度梯度可达9 ℃,当上部结构上下行分幅布置时,外侧腹板和内侧腹板有不可忽略的横向温差。
大尺寸混凝土箱梁;温度分布;温度梯度;横向温差;挠度曲率
近几十年来,全球相继发生多起由温度应力导致混凝土桥梁的严重裂损事故,研究结果表明[1−5],太阳辐射引起的温差应力是其产生的主要原因。国内外许多学者基于工程热传导理论和现场实测数据,对混凝土箱梁在太阳辐射作用下的温度分布、影响因素及分析方法进行了大量的研究,如Elbadry等[3,6]提出了全面考虑太阳辐射、大气温度、风速、桥址及桥梁走向和材料物理特性等因素影响的箱梁温度场分布的二维有限元计算方法;Mirambell等[7]基于有限差分法和有限元法提出了 2种计算桥梁温度分布的数值方法;Larsson等[8]通过对混凝土板的野外现场实验,论证了基于气象参数的有限元模型的可行性,最后运用当地气象站记录的气象数据对混凝土板的温度场进行了仿真模拟,估算了50年一遇的温度梯度极值,并与欧洲规范进行了对比评述;肖建庄等[9−11]也均基于热传导理论建立了箱梁温度场的有限元计算方法;Roberts-Wollman等[12]在2.5 a的混凝土箱梁温度场实测资料的基础上,提出了预测箱梁竖向温差的方法,并与实测值及规范规定的温度梯度进行了比较;Mondal等[13]对美国一座预应力桥梁进行了长达 5 a的温度监测,对箱梁最大竖向温差和箱梁内空气温度的关系进行了回归分析;雷笑等[1−2,14]对国内一些混凝土箱梁桥进行了温度观测,并分别提出了各自观测桥梁的温度分布形式。这些学者的研究者重点是箱梁温度场的数值模拟计算和基于实测数据的箱梁温度梯度的分析,而涉及大尺寸混凝土箱梁温度场分布的研究较少,但Li等[15]通过对加拿大的1座跨海大桥的温度实测研究表明:对于大尺寸箱梁计算来说,现有规范规定的温度梯度分布模式不够准确。本文作者基于苏通大桥辅助航道桥运营期的实测温度数据,分析了大尺寸箱梁温度场的分布特点,并基于桥址逐时实测气象数据建立了考虑了太阳辐射、结构几何尺寸、所处地理位置、桥梁方位和所用材料物理特性等因素的混凝土箱梁温度场有限元模型,对大尺寸混凝土箱梁的温度场分布以及其影响因素进行研究。
1 箱梁温度场的观测及数据分析
1.1 观测截面及测点布置
苏通大桥辅航道桥位于南通市和苏州(常熟)市之间,呈南北走向,轴向角为354o,位于东经121o、北纬 31.77o,其跨径布置见图 1,上部结构上下行分幅布置,主墩顶部两幅桥箱梁用横隔梁连接,两主墩与主梁固结。桥面铺装层为11 cm厚的沥青混凝土,全桥采用单箱单室直腹板混凝土结构,箱梁顶宽16.4 m,底宽7.5 m。根部梁高15 m,高跨比为1/17.9,跨中梁高4.5 m,高跨比为1/60,梁高采用1.6 次抛物线变化。
为了反映在日照等环境作用下双幅箱梁截面温度分布状态沿桥纵向不同位置、不同截面高度箱梁温度分布情况,选择2个箱梁断面为温度观测断面,断面位置和温度测点布置分别如图1~3所示。同时,为了反映箱梁温度与大气温湿度和风速的关系,在跨中断面布置了3个大气温湿度测点,在主桥桥面处布置了风速测点。

图1 箱梁温度观测截面分布示意图(单位:cm)Fig.1 Layout of measuring section

图2 T1截面测点布置(单位:cm)Fig.2 Layout of temperature sensors at T1 section
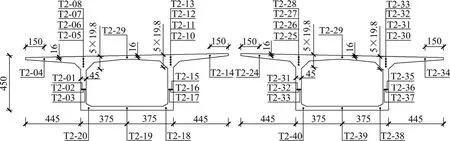
图3 T4截面测点布置(单位:cm)Fig.3 Layout of temperature sensors at T4 section
1.2 温度观测结果及分析
根据历史气象数据可知,7月为南通地区一年中较热的时间段,故本文选取2008年7月的实测温度数据为研究对象。
图4所示为T1截面的顶板混凝土实测温度。从图4可以看出:受日照辐射影响,顶板表面以下0.35m深处混凝土的温度,每天约有2 ℃的波动,顶板表面以下0.69 m和1.02 m深处的混凝土温度在1 d内波动微小,且顶板在夜间没有出现负温差现象。
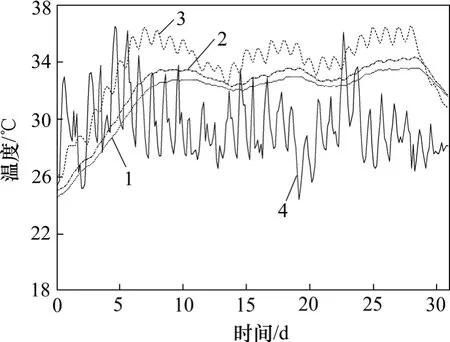
图4 顶板混凝土实测温度−时间曲线Fig.4 Curves of measured temperature−time in upper plate of box girder
图5所示为T1截面外侧(西)腹板混凝土的实测温度。从图5可知:受日照辐射和日落降温的作用,最靠近表面的1号测点温度在1 d内波动较大,约为 3℃;腹板沿壁厚方向一般在白天出现正温差现象,在夜间出现负温差现象。图6所示为T1截面的外侧(东)腹板混凝土的实测温度。实测结果表明:外侧(东)腹板混凝土温度整体略低于上游幅箱梁外侧(西)腹板混凝土温度,但变化趋势基本一样。图7所示为T1截面的内侧腹板混凝土的实测温度。从图7可以看出:内侧腹板混凝土温度整体比外侧腹板的温度低;内侧腹板温度在1 d内波动也很小。
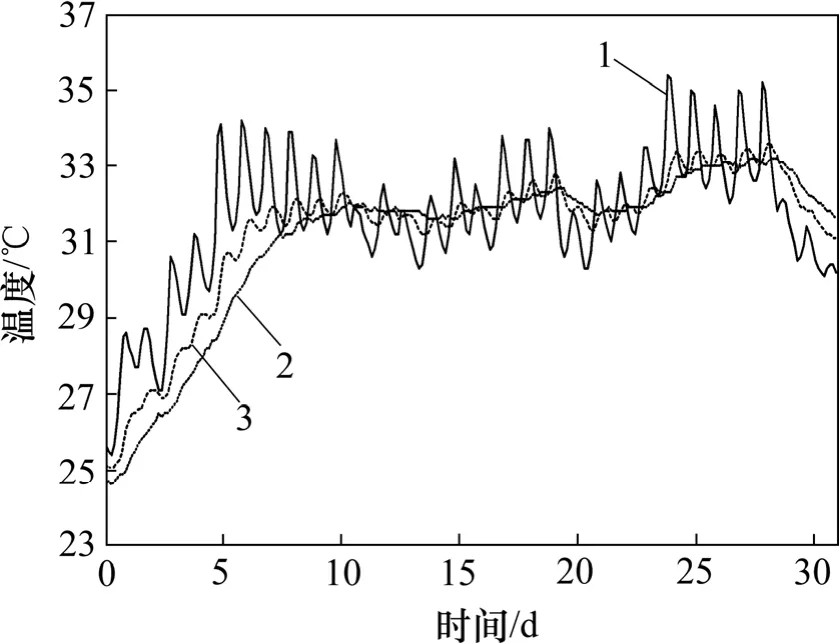
图5 外侧腹板(西)混凝土实测温度−时间曲线Fig.5 Curves of measured temperature−time in outside web(west) of box girder

图6 外侧腹板(东)混凝土实测温度−时间曲线Fig.6 Curves of measured temperature−time in outside web(east) of box girder
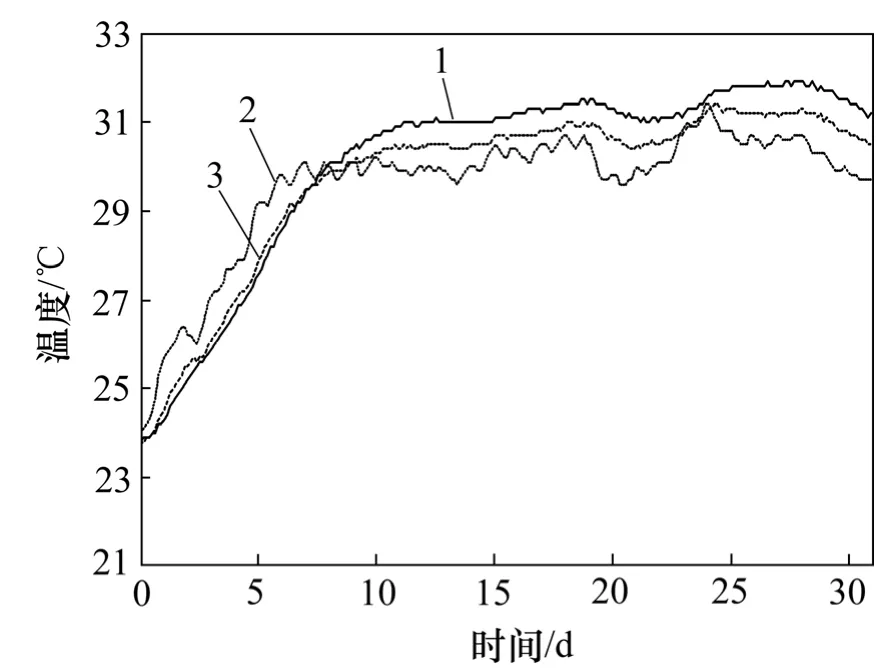
图7 内侧腹板混凝土实测温度−时间曲线Fig.7 Curves of measured temperature−time in inside web of box girder
图8所示为T1截面的底板混凝土实测温度。从图8可知:底板的温度整体低于腹板温度;在温度上升阶段,底板沿壁厚方向存在较大的温度梯度。
图 9所示为腹板平均温度与底板平均温度的对比。从图9可以看出:东侧和西侧的腹板混凝土的平均温度远大于底板的平均温度,最高温差可达4.5 ℃;而内侧腹板混凝土的平均温度也大于底板的平均温度,最大温差为1.7 ℃,发生的时间均为温度上升阶段的末期。
从以上分析来看,大尺寸双幅箱梁的温度场分布与《公路桥规》和《铁路桥规》的规定有所不同,主要表现为:外侧腹板受日照辐射影响,沿壁厚方向存在较大的正温差现象;外侧腹板和内侧腹板存在 2~3 ℃的横向温差;底板与腹板之间存在负温差现象,特别是温度上升阶段的末期较大。

图8 底板混凝土实测温度−时间曲线Fig.8 Curves of measured temperature−time in bottom plate of box girder
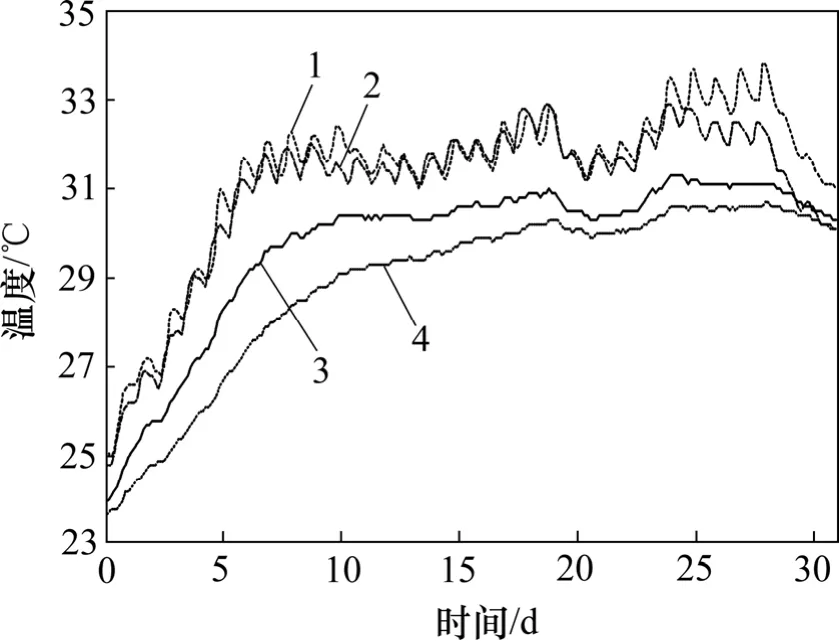
图9 腹板平均温度和底板平均温度的比较Fig.9 Comparison of web average temperature and bottom plate average temperature
由于温度测点布置有限,为了弄清大尺寸箱梁温度场的分布特点及其对混凝土箱梁温度效应产生的影响,需借助有限元对箱梁的温度场进行仿真分析。
2 有限元模型的建立
2.1 边界条件
混凝土箱梁与环境热交换示意图如图10所示。在日照作用下,混凝土箱梁与外界的热交换不仅有来自太阳的短波辐射,也有与周围环境之间的对流和长波

图10 混凝土箱梁与环境热交换示意图Fig.10 Heat transfer between concrete box girder and environment
辐射热交换。箱梁外表面热平衡可由下式表示:

式中:qS为箱梁外表面所吸收的太阳辐射热流密度;qR为箱梁外表面所吸收的地表反射的太阳辐射热流密度;qB为箱梁外表面所吸收的大气辐射热流密度;qG为箱梁外表面所吸收的地表辐射热流密度;qCa为箱梁外表面与大气对流换热的热流密度;qRa为箱梁外表面向周围环境发出的辐射热流密度。
箱梁外表面所吸收的太阳辐射热流密度由太阳直接辐射和太阳散射辐射组成,可以表示为

式中:a为箱梁外表面短波吸收系数;β为太阳高度角;IB和ID分别为晴天条件下水平面太阳直接辐射强度和散射辐射强度,具体计算见文献[16];θ和η分别为阳光对箱梁表面的入射角和箱梁表面的倾角。
投射到箱梁表面的地表反射qR可由下式计算:

式中:ξe为地面短波反射率,文献[17]给出的水面反射率经拟合可以表示为
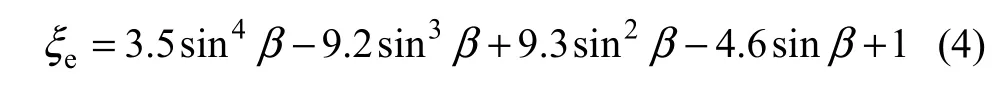
大气辐射具有灰体辐射的特性,无云天箱梁外表面所吸收的大气辐射热流密度qB的公式为
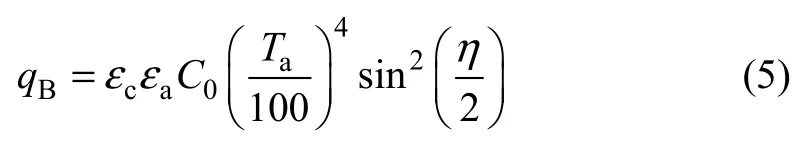
式中:εc为箱梁表面长波辐射系数;εa为大气辐射系数,取值范围为0.5~0.9;C0为黑体辐射系数;Ta为大气温度,K。
箱梁外表面所吸收的地表辐射热流密度 qG可以表示为
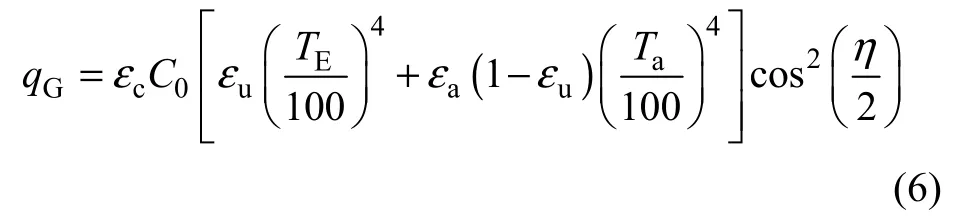
式中:εu为地表的辐射系数;TE为地表温度,K。
箱梁外表面与大气对流换热的热流密度 qCa可表示为

式中:Ts为箱梁外表面温度,K;hc为热交换系数,通常由试验来确定或按经验公式计算。在土木工程中,可按下式计算[4]:
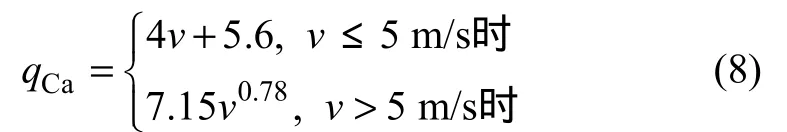
式中:v为风速,m/s。
箱梁向外界发出的热辐射可以表示为
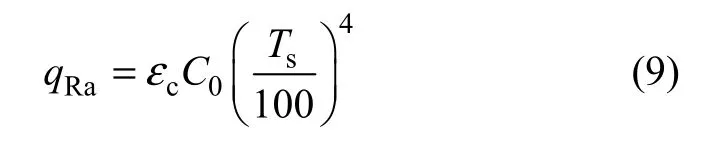
关于太阳位置参数、太阳在箱梁表面的入射角以及悬臂板在腹板上的阴影长度等计算,见文献[17]。
2.2 模型参数取值
沥青混凝土表面和混凝土表面对的太阳辐射吸收率[17]分别取为0.9和0.6,对长波辐射的吸收率分别取为0.9和0.88。沥青混凝土和混凝土热力学参数见表1。

表1 材料热力学参数Table 1 Material thermodynamics parameters
大气辐射系数取为0.82,江水辐射系数参照文献[17]取为0.96,江水温度参照文献[18]近似地取为恒定值24 ℃。
本文以天气较为晴朗的 2008−07−02—07−07这6 d为计算时间,对后3 d进行温度场模拟,其中前3 d为渡越时间,以获取较为准确的初始温度场。研究时段的风速变化和环境温度变化分别见图11和图12。
2.3 模型验证
采用软件ANSYS来进行箱梁温度场的计算分析,选用的4个二维节点热实体单元plane55可以模拟沥青混凝土和混凝土的传热。
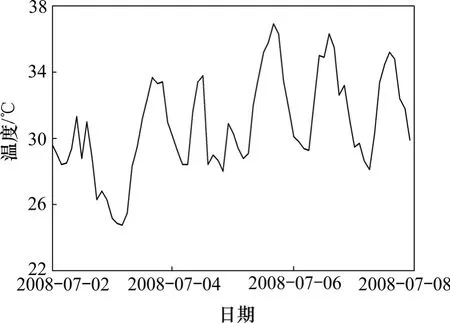
图11 实测环境温度−时间曲线Fig.11 Curves of measured ambient temperature−time

图12 风速变化时程图Fig.12 Curves of wind speed−time
经有限元求解,可得每一时刻箱梁的温度场。T1截面的顶板、腹板和底板等处测点的计算温度和实测温度变化如图13~15所示。从图13~15可知:计算温度与实测温度吻合均良好,两者不仅在规律上相似,且误差也均在0.5 ℃之内,这说明基于桥址逐时实测气象数据建立的有限元模型可以准确模拟箱梁实际温度场。

图13 顶板计算温度和实测温度变化时程图Fig.13 Calculated value and measured value of temperature at various positions in upper plate of box girder

图14 内侧腹板测点计算温度和实测温度变化时程图Fig.14 Calculated value and measured value of temperature at various positions in inside web of box girder
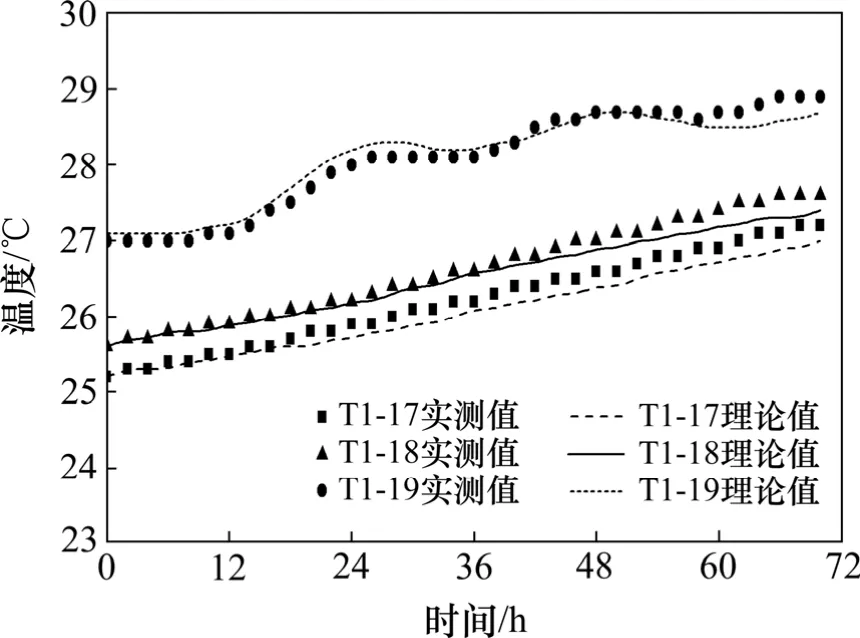
图15 底板计算温度和实测温度变化时程图Fig.15 Calculated value and measured value of temperature at various positions in bottom plate of box girder
3 箱梁温度场分析
为了分析箱梁不同高度,腹板厚度和底板厚度对箱梁温度场的影响,除计算T1和T4截面的温度场外,本文又选取北主墩以南40 m和88 m的箱梁截面进行了计算,分别简称为T2和T3截面,截面尺寸如图16所示。
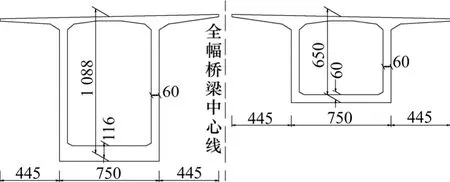
图16 箱梁截面尺寸(单位:cm)Fig.16 Section size of concrete box girder
3.1 沿截面高度方向的温度场
研究竖向温度梯度模式时,顶板温度采用腹板上方顶板沿截面深度方向的平均温度,腹板温度采用内侧腹板与外侧腹板沿截面深度方向的平均温度,底板温度采用沿截面深度方向的平均值。将有限元计算结果进行整理后,各截面沿竖向温度分布如图17所示。从图17可以看出:除底板外,箱梁的最低温度一般出现在梗腋部位,腹板下面较深的部位受日照辐射影响,温度比靠近梗腋部位的腹板高2 ℃左右;腹板和底板的整体温度随其厚度增加而减小;箱梁底板外表面的温度与较深部位的腹板温度相近,但当底板较厚时,温度从底板外表面向内部迅速衰减,并小于腹板和梗腋的温度。由以上结果可知,大尺寸箱梁竖向温度梯度主要特点为:腹板温度整体高于梗腋温度,而梗腋部位的温度又均高于底板温度,底板与腹板和梗腋之间存在负温差现象。
箱梁的温度自应力可以表示为
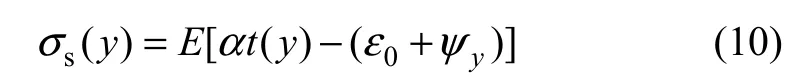
式中:t(y)为距顶板y处的温度,℃;α为材料线膨胀系数;ε0为箱梁底板外表面的变形;ψy为截面竖向挠曲变形曲率。根据平衡条件,ε0和ψy可分别表示为:

式中:b(y)为箱梁在高度y处的宽度;yc为箱梁截面质心离底板外表面的距离。
大尺寸箱梁的腹板和底板的厚度较大,占箱梁截面积的比率较高,且对箱梁沿水平向的惯性矩贡献也比较大,稍高的腹板温度和较低的底板温度可能对箱梁温度应力产生较大的影响。由于我国《公路桥规》和《铁路桥规》均没有考虑腹板和底板的温度梯度对箱梁温度效应的影响,因此,为了研究腹板和底板温度对箱梁温度效应的影响,本文采用不计腹板和底板温度梯度和考虑实际温度梯度来计算梁底应变ε0和截面竖向挠曲变形曲率ψy,计算结果如表2所示。从表2可以看出:随箱梁尺寸的增大,腹板和底板的温度对箱梁的梁底应变和截面竖向挠曲变形曲率影响也越来越大,最大误差分别可达108.8%和33.3%,由对截面竖向挠曲变形曲率ψy的影响可以推断:腹板和底板的温度对箱梁桥的挠度也会产生一定的影响。
3.2 腹板温度分布
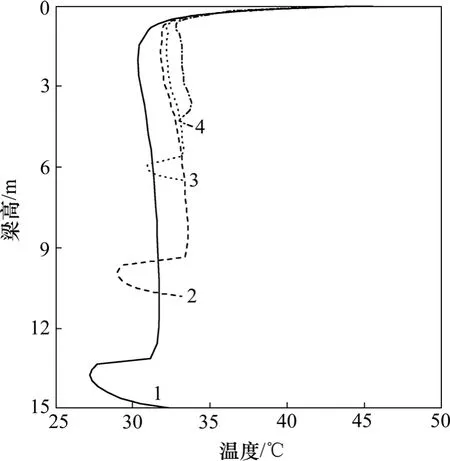
图17 各个截面沿竖向温度分布曲线Fig.17 Temperature distribution along vertical direction of each section
图 18所示为顶板温差最大时刻各截面腹板沿截面高度的平均温度分布情况。从图18可知:当箱梁尺寸较大时腹板温度分布规律为:靠近梗腋部位的温度基本不变,自顶板以下3.0~6.5 m,腹板温度基本呈线性递增趋势,并在6.5 m以下趋于恒定值;腹板底部的温度一般比梗腋处高2 ℃左右。根据腹板温度分布规律,建议大尺度箱梁腹板温度分布的模式可修正为:

式中:tg为梗腋部位温度,℃;L为箱梁的悬臂长度;y为计算点离顶板的距离。
图 19所示为顶板温差最大时刻各截面箱梁腹板沿壁厚方向的温度分布情况。从图19可以看出:箱梁外侧西边腹板受下午太阳辐射的影响,存在较大的温度梯度,最大可达9 ℃,温度梯度与箱梁的高度和腹板的厚度均呈正相关关系,箱梁内侧腹板温度梯度较小,整体温度也低于外侧腹板。为研究内外侧腹板横向温差的影响,利用式(10)~(12)可计算出腹板外侧最大的自应力和箱梁的横向挠曲变形曲率,如表3所示。从表3可以看出:当箱梁高度较高,腹板较厚时,由内侧和外侧腹板温差引起的最大自应力可达3.2 MPa,而且引起的横向挠曲变形曲率也与由箱梁竖向温差引起的竖向挠曲变形曲率相当。

表 2 ε0和 ψy计算值Table 2 Calculated value of ε0 and ψy

图18 各个截面腹板沿竖向温度分布曲线Fig.18 Curves of web temperature distribution along vertical direction of each section
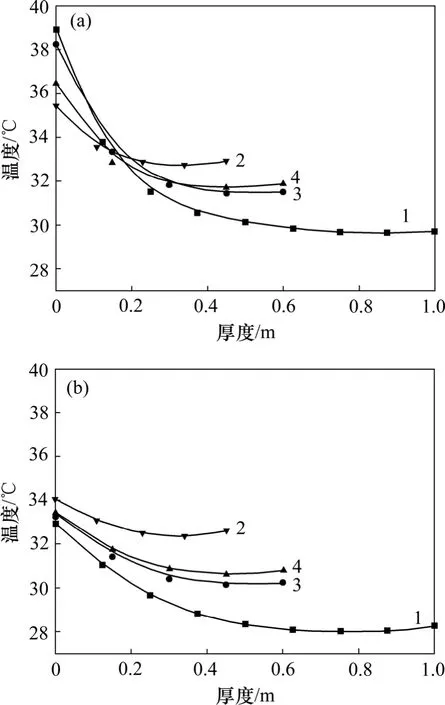
图19 各个截面腹板壁厚方向温度分布曲线Fig.19 Temperature distribution along web of section
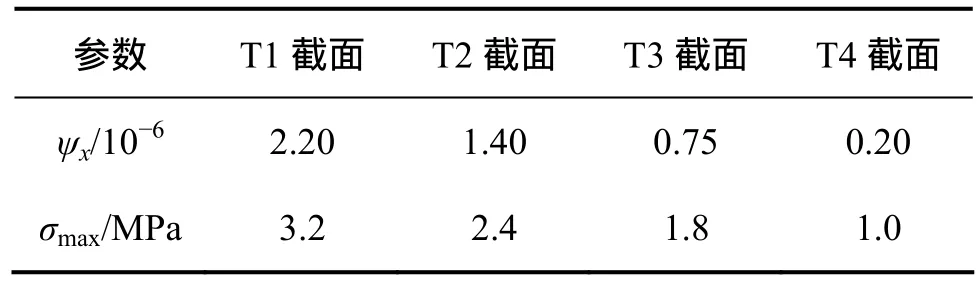
表 3 σmax和 ψx计算值Table 3 Calculated value of σmax and ψx
3.3 底板沿壁厚方向温度分布研究
顶板温差最大时各截面底板沿壁厚方向温度分布如图20所示。可见:底板外表面温度随底板厚度变化不大,温度较低部位一般发生在距底板外表面 0.75h处;底板温度梯度随底板厚度增加而变大。假设底板温度分布函数为
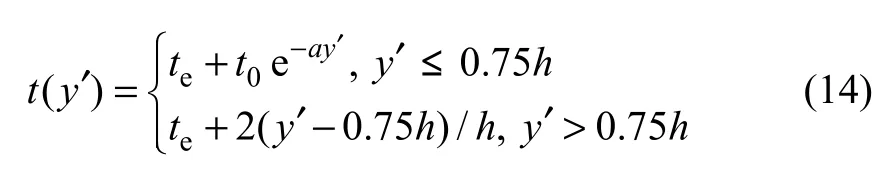
式中:te为离外面0.75h处的温度,℃;t0为温度拟合值,℃;a为温度梯度的衰减系数;y′为计算点离底板外表面距离;h为底板厚度。
拟合曲线及参数分别如图20和表4所示。从图20可以看出:温度理论值与拟合值拟合结果较好。从表4可知:底板温度梯度的衰减系数a与底板的厚度呈负相关。t0与底板的厚度呈正相关,图21所示为t0和衰减系数a与厚度的关系。从图21可以看出:当底板的厚度大于0.6 m时,底板的温度梯度以及其衰减系数与其厚度基本呈线性变化。
结合表2、表4和图17可知:当底板厚度<0.6 m时,可以不考虑底板温度的影响;当底板厚度≥0.6 m时,底板的温度分布可以表示为
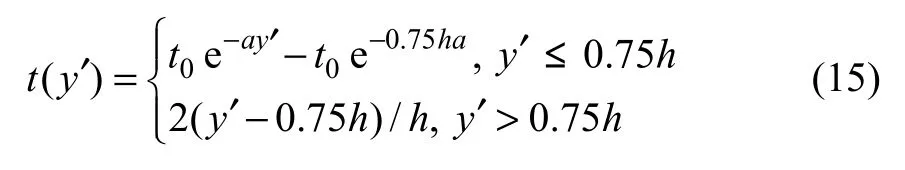
衰减系数a和温度梯度t0可拟合为式(16)和(17):


当 0.6 m≤h≤1.7 m 时,t0e−0.75ha<0.35,故式(15)可以近似为:
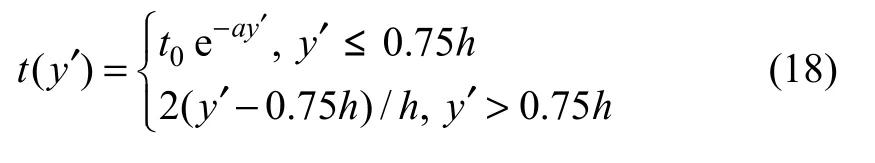

图20 底板计算温度和拟合温度沿壁厚方向分布曲线Fig.20 Curves of calculated and fitted temperature distribution along wall thickness of bottom plate

表4 底板温度分布的拟合参数Table 4 Fitting parameters of bottom plates temperature distribution
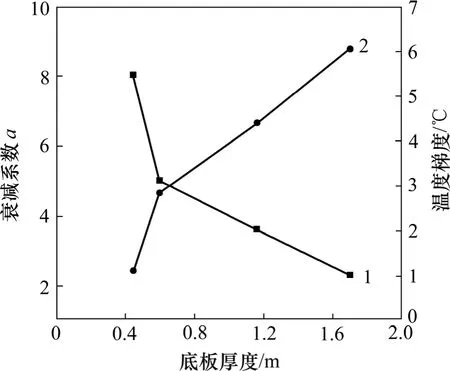
图21 底板温度梯度以及其衰减系数与底板厚度的关系Fig.21 Temperature gradient of bottom plates and its attenuation coefficient versus thickness of bottom plates
4 结语
(1) 大尺寸箱梁沿截面高度方向的温度分布模式不同于规范中的规定,其主要特点为:腹板温度整体高于梗腋温度,而梗腋部位的温度均高于底板温度,底板与腹板和梗腋之间存在负温差现象。
(2) 大尺寸箱梁腹板和底板温度梯度对箱梁的温度效应产生重要影响,故在施工监控时应对大尺度箱梁的温度梯度进行修正,以对温度效应获得较准确的预测。
(3) 由于大尺寸箱梁的高度较高,其腹板大部分处于太阳照射之下,沿壁厚方向可产生较大的温度梯度,沿壁厚方向的温度梯度可达9 ℃;当上部结构上下行分幅布置时,外侧腹板和内侧腹板之间存在较大的横向很差,由这横向温差引起的最大自应力可达3.2 MPa,而且引起的横向挠曲变形曲率也与由箱梁竖向温差引起的竖向挠曲变形曲率相当。
[1] 雷笑, 叶见曙, 王毅, 等. 基于长期观测的混凝土箱梁温度与应变分析[J]. 江苏大学学报: 自然科学版, 2010, 31(2):230−234, 239.
LEI Xiao, YE Jianshu, WANG Yi, et al. Analysis of concrete box-girder temperature and strain based on long term observation[J]. Journal of Jiangsu University: Natural Science Edition, 2010, 31(2): 230−234, 239.
[2] 张亮亮, 杨磊, 杨转运, 等. 大跨混凝土箱梁温度场分析[J].土木建筑与环境工程, 2011, 33(1): 36−42.
ZHANG Liangliang, YANG Lei, YANG Zhuanyun, et al.Temperature Field Analysis of Long-span Concrete Box Girders[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(1): 36−42.
[3] Elbadry M M, Ghail A. Temperature variations in concrete bridges[J]. Journal of the Structural Engineering, 1983, 109(10):2355−2374.
[4] Saetta A, Scotta R, Vitaliani R. Stress analysis of concrete structures subjected to variable thermal loads[J]. Journal of Structural Engineering, 1995, 121(3): 446−457.
[5] 韩大建, 谭毅平. 预应力混凝土单室箱梁桥的温度变化[J].四川大学学报: 工程科学版, 2008, 40(6): 7−13.
HAN Dajian, TAN Yiping. Temperature variation in pre-stressed concrete single-cell box-girder bridges[J]. Journal of Sichuan University: Engineering Science Edition, 2008, 40(6): 7−13.
[6] Branco F A, Mendes P A. Thermal actions for concrete bridge design[J]. Journal of Structural Engineering, 1993, 119(8):2313−2331.
[7] Mirambell E, Aguado A. Temperature and stress distributions in concrete box girder bridges[J]. Journal of Structural Engineering,1990, 116(9): 2388−2409.
[8] Larsson O, Thelandersson S. Estimating extreme values of thermal gradients in concrete structures[J]. Materials and Structures, 2011, 44(8): 1491−1500.
[9] 肖建庄, 宋志文, 赵勇, 等. 基于气象参数的混凝土结构日照温度作用分析[J]. 土木工程学报, 2010(4): 30−36.
XIAO Jianzhuang, SONG Zhiwen, ZHAO Yong, et al. Analysis of solar temperature action for concrete structure based on meteorological parameters[J]. China Civil Engineering Journal,2010(4): 30−36.
[10] 汪剑, 方志. 混凝土箱梁桥的温度场分析[J]. 湖南大学学报:自然科学版, 2008(4): 23−28.
WANG Jian, FANG Zhi. Temperature variation of concrete box girder bridge[J]. Journal of Hunan University: Natural Sciences,2008(4): 23−28.
[11] 王卫锋, 陈国雄, 马文田. 混凝土连续刚构桥箱梁的温度监测与分析[J]. 华南理工大学学报: 自然科学版, 2007(2):69−74.
WANG Weifeng, CHEN Guoxiong, MA Wentian. Monitoring and analysis of temperature for concrete box girder in continuous rigid frame bridge[J]. Journal of South China University of Technology: Natural Science Edition, 2007(2): 69−74.
[12] Roberis-Wollman C L, Breen J E, Cawrse J. Measurements of thermal gradients and their effects on segmental concrete bridge[J]. Journal of Bridge Engineering, 2002, 7(3): 166−174.
[13] Mondal P, DeWolf J T. Development of computer-based system for the temperature monitoring of a post-tensioned segmental concrete box-girder bridge[J]. Computer-Aided Civil and Infrastructure Engineering, 2007, 22(1): 65−77.
[14] 方志, 汪剑. 大跨预应力混凝土连续箱梁桥日照温差效应[J].中国公路学报, 2007, 20(1): 62−67.
FANG Zhi, WANG Jian. Sun light thermal difference effect on long-span PC continuous box girder bridge[J]. China Journal of Highway and Transport, 2007, 20(1): 62−67.
[15] Li D N, Maes M A, Dilger W H. Thermal design criteria for deep prestressed concrete girders based on data from confederation bridge[J]. Canadian Journal of Civil Engineering, 2004, 31(5):813−825.
[16] Muneer T, Gui M S. Evaluation of sunshine and cloud cover based models for generating solar radiation data[J]. Energy Conversion and Management, 2000, 41(5): 461−482.
[17] Kehlbeck F. 太阳辐射对桥梁结构的影响[M]. 刘兴法, 译. 北京: 中国铁道出版社, 1981: 9−29.
Kehlbeck F. Influence of bridge structure caused by solar radiation[M]. LIU Xing-fa, trans. Beijing: China Rail-way Publishing House, 1981: 9−29.
[18] 孙大明, 田慧峰, 张欢, 等. 长江上游水温监测及水温和气温关系研究[J]. 建筑节能, 2010, 38(12): 74−77.
SUN Daming, TIAN Huifeng, ZHANG Huan, et al. Monitoring of water temperature and changing relationship between the water temperature and air temperature in the upper Yangtze River[J]. Building Energy Efficiency, 2010, 38(12): 74−77.
(编辑 赵俊)
Measurement and simulation on solar temperature field of large size concrete box girder
GU Bin1, CHEN Zhijian2, CHEN Xindi3
(1. College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China;2. School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China;3. College of Harbour, Costal and Offshore Engineering, Hohai University, Nanjing 210098, China)
Based on analysis of measured temperature of auxiliary shipping channel bridge of the Sutong bridge during the operation period and simulation calculation of temperature field of concrete box girder with different size cross section, the characteristics of temperature distribution of large size concrete box girder and its effect were analyzed. A correction method of web and bottom plate temperature gradient was proposed. The results show that the temperature of web is higher than that of the haunch, and the temperature of haunch is mostly higher than that of the bottom plate. The maximum error of vertical deflection curvature caused by the temperature of web and bottom plate can reach 33%. The temperature gradient along the thickness direction of web can reach 9 ℃. When the concrete box girder structure is arranged separately, the effect of transverse temperature difference caused by inside web and outside web cannot be neglected.
large size concrete box girder; temperature distribution; temperature gradient; transverse temperature difference; deflection curvature
U448.35
A
1672−7207(2013)03−1252−10
2012−03−12;
2012−06−04
江苏省交通科学研究规划项目(08Y60)
顾斌(1986−),男,江苏淮安人,博士研究生,从事大跨径桥梁的安全监控研究;电话:15950579224;E-mail: hhgbhh@sina.cn
