基于神经网络方法的土壤流失量预测研究

钱爱国，高 荣，彭 琦

(1．中国水电顾问集团 华东勘测设计研究院，浙江 杭州310014;2．深圳地铁集团 深圳市政设计研究院有限公司，广东 深圳518029)

(责任编辑 赵文礼)

土壤流失量预测是生产建设项目水土保持方案编制的重点之一，其准确与否直接影响到对生产建设项目的水土保持分析、评价和防治措施体系的布局，并间接影响水土保持投资估算和效益分析的准确性。

生产建设项目土壤流失量预测方法主要有类比法、数学模型法和试验观测法等。尽管方法很多，但由于生产建设项目土壤流失的影响因子多且因子之间的耦合关系难以确定，各种土壤流失量的预测方法均存在一定的局限性和不合理性，从而使得土壤流失量的准确预测成了业内关注的重点和难点［1］。目前，生产建设项目土壤流失量预测通常选取项目建设区附近某一个或两个同类建设项目作为类比工程，线性类比两个项目各预测单元的土壤流失主导因子后确定修正系数，对类比工程的监测成果进行修正后确定预测单元的土壤侵蚀模数。此法虽显直观，但受限于类比工程的可比性以及无法准确反映不同建设项目土壤流失影响因子的差异，使得该法不仅在理论上缺乏严谨，而且也常因类比工程可比性差而显得牵强。本研究将人工神经网络的BP 算法引入生产建设项目土壤流失量预测，将降雨侵蚀力、土壤可蚀性、坡长和坡度、水土保持措施等作为影响土壤流失量的主导因子，并根据大量的生产建设项目水土保持监测实例，初步建立了基于人工神经网络方法的土壤流失量预测系统，旨在探索一种新的生产建设项目土壤流失量预测方法。

1 人工神经网络简介

人工神经网络思想具有超强的自学习功能，对于预测有特别重要的意义，因此在多元非线性的预测问题中得到了广泛应用［2］。

人工神经网络是以对大脑的生理研究成果为基础的，其目的在于模拟大脑的某些机理与机制，实现某个方面的功能。人工神经网络具有如下突出优点［2-4］:①可以充分逼近任意复杂的非线性关系;②所有定量或定性的信息都等势分布贮存于网络内的各神经元，故有很强的鲁棒性和容错性;③采用并行分布处理方法，使得快速进行大量运算成为可能;④可学习和自适应不知道或不确定的系统;⑤能够同时处理定量、定性问题。

基于误差反向传播的多层前馈网络(Error Back Propagation，简称BP)，是目前运用最多最成功的人工神经网络之一，其拓扑结构如图1 所示，一般分为输入层、隐含层、输出层三层网络。BP 网络的权值学习常采用误差逆传播学习算法，建立BP 网络过程分为网络训练及网络工作2 个阶段:在网络训练阶段，根据给定的训练模式，按照“模式顺传播→误差逆传播→记忆训练→学习收敛”4 个过程进行网络权值(包括阈值)的训练;在网络工作阶段，根据训练好的网络权值及给定的输入向量，按照“模式顺传播”方式求得与输入向量相对应的输出向量的解答［2］。

图1 BP 神经网络典型拓扑结构

人工神经网络能够处理数据拟合和预测等问题，目前已经在很多工程建设中发挥了巨大的作用。最近，很多学者将发展和引用新的非线性理论带入神经网络模型中，以求达到更优的数学性能。如近年来发展起来的小波神经网络［5-8］，就是结合小波变换理论与人工神经网络的思想而构造的一种新的神经网络模型，具有更强的逼近和容错能力。这些新理论新方法的引进和应用，无疑给神经网络的发展注入了新的活力。

2 水土流失影响因子与数据收集

2．1 影响因子分析

通用土壤流失方程是用于定量预报农地或草地坡面多年平均年土壤流失量的一个经验性的土壤侵蚀预报模型，它是建立在自然状态或耕地径流小区试验基础上的，因此在开挖、填筑等扰动强度较大的生产建设项目土壤流失量预测中难以应用。本研究选择可直接获得且反映通用土壤流失方程中影响土壤流失量的各个主导参数作为人工神经网络的输入层，进而得出预测单元的土壤流失量。输入层的具体参数确定如下:

(1)降雨侵蚀力因子。降雨侵蚀力因子是一个地区降水侵蚀潜势的一个量度，定义为降雨动能E 和最大30 min 降水强度I30两个暴雨特征值的乘积，即EI30。由于降雨动能E 和最大30 min 降水强度I30在实际应用中较难获得，因此Wischmeier 提出了一个直接利用年平均降雨量(P)和月平均降雨量(Pi)两个参数推算降雨侵蚀力因子的经验公式［9］。鉴于同一地区的年平均降水量在短期内基本相同，无法全面反映不同生产建设项目不同预测时段之间的降雨差异，而对于单一生产建设项目而言，施工期往往跨越数个年度，月平均降雨量参数的获取又显得繁琐，因此本研究简略地利用预测单元所在区域预测期(或监测期)单月平均降雨量(P月)表示降雨侵蚀力因子。

(2)土壤可蚀性因子。土壤可蚀性因子即单位侵蚀力所产生的土壤流失量，在通用土壤流失方程中该值的获取是在坡长22．1m、宽1．83m、坡度为9%的径流小区内测定的(小区完全裸露且无水土保持措施)。由于生产建设项目中土壤的粒径组成、有机质、土壤入渗等多种资料较难获得，Shiraz 等提出并经验证仅考虑土壤几何平均粒径(Dg)即可计算土壤可蚀性［9］。本研究的土壤可蚀性因子也直接用Dg表示。

(3)坡长、坡度因子。坡长、坡度因子为复合因子，即当径流小区的坡长L=22．1m、坡度S=9%时，LS为1，完全平坦的地面LS=0。根据国内外学者多年的研究，本研究中的坡度S 采用刘宝元等［9］提出的陡坡公式，利用预测单元的坡度(θ)表示;坡长采用USLE公式中预测单元的坡长(λ)表示。

(4)水土保持措施因子。施工期水土保持措施的实施可极大地减少水土流失。施工过程中无任何水土保持措施，其水土保持措施因子(C)值为1;若场地全部硬化，则水土保持措施因子(C)值为0;如有相关水土保持措施因子，根据其防护效果，在0 ＜C ＜1 范围内取值。

根据上述分析，本研究输入层指标主要包括5 个参数，输入层参数及数据来源见表1。

表1 输入层各参数及数据来源

2．2 数据收集

广泛收集国内各类工程水土保持监测的实测数据，监测单元包括路基边坡、堆土边坡、施工场地和弃渣场等，数据库包含17 个工程实例的监测数据(表2)。

3 水土流失量BP 神经网络模型

3．1 预测模型的建立

确定影响土壤流失量的主导因子后，运用人工神经网络方法建立土壤流失量预测模型的步骤如下:

(1)输入层的确定。输入层为土壤流失量的主要影响因素，其神经元个数为5，分别为预测期(或监测期)单月平均降雨量(P月)、土壤几何平均粒径(Dg)、预测单元的坡度(θ)、预测单元的坡长(λ)和水土保持措施因子(C)。

(2)确定神经网络的结构。包括隐含层层数和单元个数以及输出层的单元个数和期望输出。输出层为预测目标，即土壤流失量，单元个数为1。经测试，隐含层层数为1。预测模型中输入层、隐含层和输出层单元个数分别为5、10、1。

(3)依据表2 收集的国内生产建设项目土壤流失量监测数据，建立学习与检测样本，对神经网络模型进行学习和训练，确定神经网络的连接参数和阈值，并运用检测样本进行测试，检验预测模型的准确性。

为了保证神经网络收敛速度，需要输入层和输出层数值在0 ～1 之间，因此需要对数据进行归一化处理。进行归一化处理采用如下公式

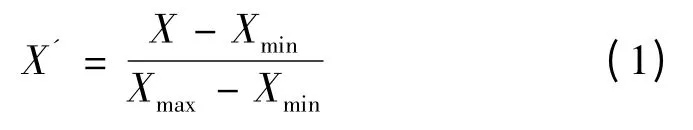
式中:X'为归一化后的数值;Xmax、Xmin分别为数组中最大值和最小值。

表2 部分国内生产建设项目土壤流失量监测数据

3．2 数据结果分析

表2 中的工程实例，前14 个样本作为学习样本，后3 个样本作为检测样本。运用MATLAB 软件编制的神经网络程序对学习样本进行了训练，学习样本的拟合结果见图2。从图2 看出，预测值和实测值的散点图基本分布在Y =X 这条直线周围，说明拟合精度非常高，也证明了建立的神经网络模型在数据拟合上的巨大优势。用检测样本对神经网络预测模型的有效性和准确性进行验证，结果如表3。由表3 知，3 个检测样本的预测误差均小于15%，预测精度较高，能够满足工程应用需要。

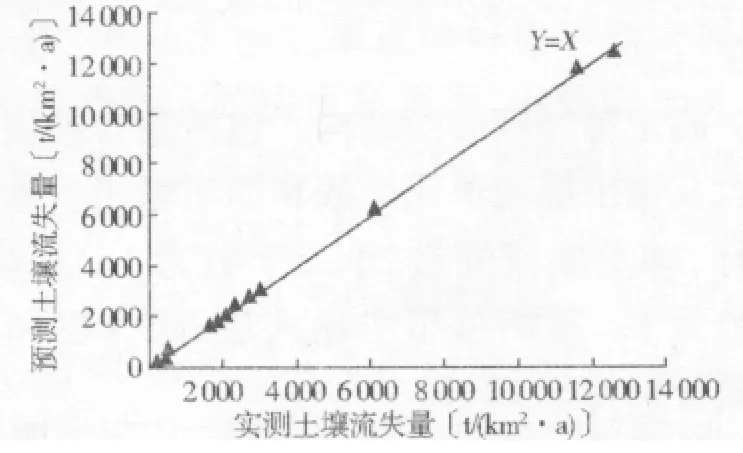
图2 模型预测值与实测值比较

表3 检测样本判定结果对比

4 结 语

(1)影响生产建设项目土壤流失量的因素繁多，每个因素与土壤流失量的关系又难以准确确定，加上各因素之间存在的各种耦合关系，导致土壤流失量的预测成为一个高度复杂的多元非线性问题，常规的预测方法因其局限性、不合理性以及精度差等问题，往往难以实现准确预测。本研究创造性地将人工神经网络的BP 算法引入到生产建设项目土壤流失量预测中，充分发挥人工神经网络较强的自学习和逼近能力，将降雨侵蚀力、土壤可蚀性、坡长、坡度和水土保持措施因子等作为土壤流失量的主要影响因子，将收集到的17 个工程土壤流失量监测实例作为学习样本和检测样本，建立了土壤流失量的神经网络预测模型。预测结果表明，该模型拟合和预测精度高，具有很强的应用价值，能够满足工程应用需要。

(2)一个网络结构优良、预测精度高的神经网络模型需要种类齐全、数量众多的样本作为数据支撑，这样才能保证所建立的神经网络模型随机性小，并降低其预测数据的波动性。因此，要在土壤流失量预测中利用好神经网络这一工具，一方面要求我们加强对土壤流失规律的研究，将更多独立、易采集且直接影响土壤流失产生的因子引入到神经网络模型中来，另一方面需要我们加强对生产建设项目水土保持的监测，更加广泛地积累土壤流失量监测数据，不断扩展预测模型的数据库系统，实现神经网络预测模型的持续完善。

［1］潘献鸿，李海林，高荣．类比法预测建设项目水土流失量［J］．水土保持应用技术，2009(6):14-16．

［2］王伟．人工神经网络原理［M］．北京:北京航空航天大学出版社，1995:2-45．

［3］郭雷，李夕兵，岩小明，等．基于BP 网络理论的岩爆预测方法［J］．工业安全与环保，2005，31(10):32-34．

［4］桂现才．BP 神经网络在MATLAB 上的实现与应用［J］．湛江师范学院学报，2004，25(3):79-89．

［5］刘洪波，张宏伟，闫晓强．城市供水管网水量预测的小波神经网络方法［J］．天津大学学报，2005，38(7):636-639．

［6］马涛，徐向东．基于小波网模型的区域供热系统负荷预测［J］．清华大学学报，2005，45(5):708-710．

［7］彭琦，张茹，谢和平，等．基于AE 时间序列的岩爆预测模型研究［J］．岩土力学，2009，30(5):1436-1440．

［8］彭琦，钱爱国，肖钰．基于人工智能方法的岩爆预测系统［J］．四川大学学报:工程科学版，2010(4):18-25．

［9］刘秉正，吴发启．土壤侵蚀［M］．西安:陕西人民出版社，1996:75-83．