水体中叶绿素a含量短周期预测的研究
2013-02-01李鹏程纪晓亮张明华
李鹏程,纪晓亮,梅 琨,张明华,2
(1.温州医学院 温州市水域科学与环境生态重点实验室,浙江 温州 325035;2.University of California Land,Air and Water Resources Department,Davis CA 95616)
水体中叶绿素a含量短周期预测的研究
李鹏程1,纪晓亮1,梅 琨1,张明华1,2
(1.温州医学院 温州市水域科学与环境生态重点实验室,浙江 温州 325035;2.University of California Land,Air and Water Resources Department,Davis CA 95616)
通过连续监测数据分别使用线性回归方法和人工神经网络方法建立叶绿素a在短周期内的同步和6步超前预测模型,探讨在短周期内建立叶绿素a含量预测模型的可行性,从而对可能发生的“水华”现象做出前瞻性预测。同时,通过对建立的线性回归模型和人工神经网络模型进行比较,发现人工神经网络在预测精度方面较线性模型有一定优势。
逐步线性回归;人工神经网络;叶绿素a
夏季有充足的光照条件和适宜藻类生长、繁殖的水体温度,藻类繁殖比较迅速。罗固源等[1]对临江河回水区的研究表明,该地区藻类大面积暴发集中5-6月。温瑞塘河流速非常慢,可能导致氮、磷等营养物质在部分地区聚集,造成水体富营养化加剧,甚至出现 “水华”现象[2-4],如果出现能够分泌毒素的蓝藻,还将对公众健康构成威胁,因此,研究能够预测水体藻类暴发的技术是十分必要的[5-8]。事实上,很多研究者已经利用各种技术和跨年度的监测数据对水体中叶绿素a的变化进行了预测,如王飞儿等[9]利用对千岛湖1999-2000年的监测资料,对千岛湖的叶绿素a变化进行研究,结果表明,5-7月藻类的繁殖最为旺盛,容易发生“水华”现象。对水体中叶绿素a的日变化研究,将有助于细化这种预测工作,为此,本研究使用Matlab软件对24 h连续监测数据进行分析,对叶绿素a在小尺度范围内随相关因素的变化情况进行拟合和预测。现将有关结果报道如下。
1 数据来源和研究方法
1.1 数据来源
温瑞塘河位于瓯江以南、飞云江以北的温瑞平原,是温州市境内十分重要的河道水系。温瑞平原对温州的经济和社会发展起着十分重要的作用,但伴随着工农业发展,温瑞塘河却受到了较为严重的污染,具体表现为富营养化程度高,一些水质指标异常。虽然,当地政府早已意识到这一问题,并实施了一系列治理措施,但由于温瑞塘河极低的流速,以及营养物质的不断进入和积累,河段处于富营养化状态。据2006年4月浙江省水资源监测中心温州分中心监测数据,温州市区28条内河37个断面所有断面水质为劣Ⅴ类,其中氨氮量均超标14.59 倍[10]。
此次昼夜连续监测点位于三洋湿地内,采用YSI进行24 h连续监测,监测指标为叶绿素a、溶解氧、光合有效辐射、温度,以及仪器放置水深,监测时间为2012年6月13日10:30至次日10:00,YSI记录数据间隔为60 s,光通量仪的记录数据间隔为30 s,另外,每2 h使用流速仪测1次流速。
1.2 研究方法
对实验数据进行整理,由于流速过小,最大值才0.016 m·s-1,所以建模过程中不予考虑,将YSI和光通量仪所测的每5 min的数据进行平均,共得到282组数据,前252组数据用来建立预测模型,后30组数据 (即次日早晨数据)用来验证模型的预测精度 (在超前6步预测中,由于只有276组数据,故252组数据用来建立模型,24组用来验证预测),研究中,分别建立同步和6步超前线性和非线性 (神经网络)模型,对叶绿素a进行拟合和预测。
2 建立预测模型
2.1 输入数据的优化
建立模型时以光合有效辐射、溶解氧、仪器放入水深以及水温为输入变量 (6步超前预测时,加入当前叶绿素值为输入向量,处理方式和同步预测一致),记为 X1,X2,X3和 X4,X1,X2,X3,X44个282×1的列向量构成282×4的输入矩阵,对应的叶绿素a值为目标值,记为Y,Y为282×1的列向量,通过Matlab中corrcoef函数可以求得输入之间的相关矩阵E,

从E可以看出,X2和 X4高度相关,输入矩阵可以降低维数,对输入矩阵进行主成分分析,在Matlab中可由 princomp函数实现,通过该函数求得的矩阵特征值为 [2.243 1,1.097 5,0.649 2,0.010 3]T,可以计算出前3个成分包含了原始数据99.74%的信息,所以可以使用原矩阵 [,X4]乘以主成分分析所得特征向量矩阵的前三列得到新的 282 × 3 的 输 入 向 量 矩 阵 [X1′,X2′,X3′],X1′=0.343 2 X1+0.647 3 X2-0.204 8 X3+0.649 1 X4,X2′=0.603 4 X1-0.041 2 X2-0.569 7 X3-0.274 8X4,X3′=0.719 7 X1-0.286 3X2-0.569 7 X3-0.274 8X4,该向量矩阵列之间正交,且数据经过了标准化处理,对输出Y同样进行标准化处理,以保持数据的一致性。
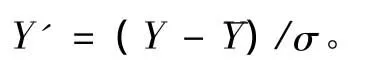
2.2 同步线性回归模型的建立
在Matlab中利用stepwise函数进行逐步回归,最终建立回归方程,校正自由度后的R2为0.924 0,经F和P检验,在显著性水平α=0.05时,回归模型显著。Y′=0.003 8+0.529 1 X1′-0.270 4 X2′-0.551 2 X3′;Y= σY′+,使用建立的方程对叶绿素a进行拟合和预测的结果如图1所示。

图1 线性回归拟合及预测的结果
从图1可以看出,拟合曲线和真实值具有相似的变化趋势,只是在变化幅度上与真实值存在一些差异,特别是预测数据部分,部分预测值偏离真实数据比较远,当然,也就意味着这些值存在较大的误差。线性回归拟合的相对误差如图2所示。
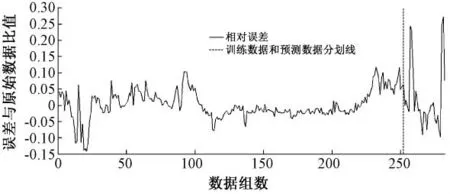
图2 线性回归拟合结果的相对误差
从图2中可以看出,用于构建预测模型的数据,拟合值误差大致在10%左右,其中整个误差曲线中部那段误差较小的部分,可能是由于夜晚少了光照条件的影响,以及白天活跃的浮游生物趋于平静所致,在这段时间内引起叶绿素a含量变化的影响因素相对单一,模型容易进行拟合,所以误差也相对较小。而预测数据中有一小部分数据偏离真实值较远,最大时偏离超过25%,但在30个预测值中仅5个数据的相对误差超过10%,其中4个超过20%,1个超过11.6%,分别位于预测数据的第5(24.3%),6(23.2%),7(11.6%),28(24.6%)和29(27.3%)处,异常点间时间差不都为2 h,可能是每隔2 h采水样过程中造成的仪器晃动,进而形成的个别点数据异常之故。
同步模型可以了解一些相对容易获得的指标就可以快速地得知叶绿素a的大致含量,而要对叶绿素a含量做出前瞻性预测,必须进行超前预测。
2.3 使用线性模型进行的超前预测
使用线性模型进行超前预测,和同步预测所不同的是,模型的输出数据为之后一段时间的叶绿素a值,实验数据为5 min 1次,实验中进行6步超前预测,即预测0.5 h以后的叶绿素a,而当前的叶绿素a值则作为输入,与其他4个输入一起组成276×5的输入矩阵,经预处理后同样有3个主成分,将前252组数据作为建立模型的训练数据,后24组数据用来检测模型的预测精度。经过逐步回归后,建立R2为0.678 6的线性回归模型 (图3)。
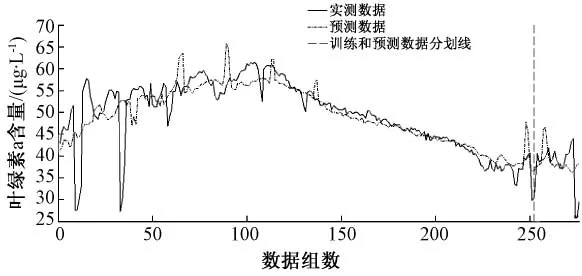
图3 线性回归6步超前的预测结果
从图3中可以看出,线性回归模型在进行6步超前预测时可以保持一定的变化趋势,但是预测曲线还是和原始数据的曲线在形状上存在一些差异,而且在部分点处存在较大的误差,误差曲线如图4所示。

图4 线性回归6步超前预测的相对误差
如图4所示,除了比较集中的少数点误差较大外,误差大概为20%,可以进行大致情况的预测,但精确度偏低。
2.4 BP神经网络同步的模型
利用Matlab神经网络工具箱建立具有3输入,7个隐含层神经元和1个输出神经元的3层BP网络,用于训练的数据和建立线性同步模型的数据相同,训练函数为trainlm,经过127步训练得到回归系数超过0.99的神经网络模型 (图5)。
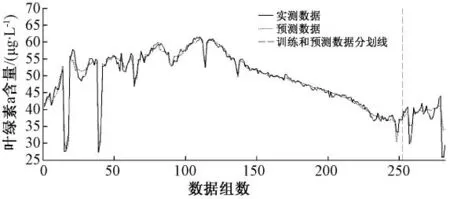
图5 BP神经网络同步的预测结果
从图5看,预测结果较好地拟合了原曲线,预测部分在叶绿素a含量变化剧烈的地方预测了正确的变化方向,但数值却相距不少,而且由于这些地方叶绿素a含量数据较小,所以产生了比较大的相对误差,相对误差曲线如图6所示。
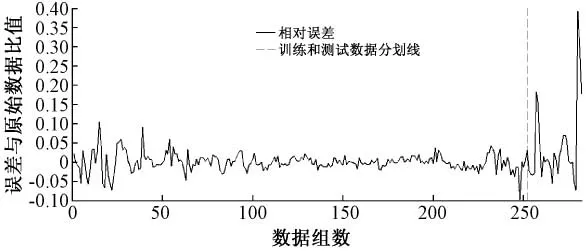
图6 BP神经网络同步预测的相对误差
从图6可知,除去少数异常数据点外,BP神经网络的预测结果相对误差5%左右,而且随着远离训练数据有逐渐增大的趋势。正如上文所述,叶绿素a在某些点剧烈变化极有可能是仪器晃动所造成的,而这种晃动,造成了仪器放入深度的变化,将仪器放入深度作为输入量使网络具有了模拟这种变化的能力,但由于具有这种变化的数据点比较少,网络对于这种变化不能充分学习,因而网络难以对这种变化产生的数值波动做出精确预测,只能做出其变化方向的预测和数值的粗略估计。而在正常数据的预测中BP神经网络预测的结果优于逐步回归预测。
2.5 使用BP神经网络进行的超前预测
建立BP神经网络超前预测模型的数据与建立线性回归模型超前预测的数据相同,利用Matlab神经网络工具箱,最终建立3输入,9个隐含层神经元,但输出的3层BP神经网络模型,其模拟结果如图7所示。
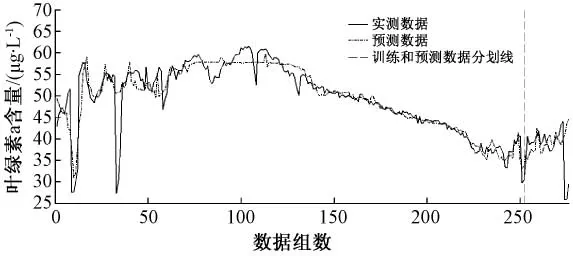
图7 BP神经网络6步超前的预测结果
如图7所示,进行6步超前预测时,模型已经很难对波动较大的数据进行拟合,而对于变化相对不怎么剧烈的数据有不错的效果,平常进行采样时,难免受各种外界因素和个人因素的影响,而这种弱化了非正常因素影响效果的数据可能更加接近真实值,其相对误差曲线如图8所示。

图8 BP网络6步提前预测的相对误差
如图8所示,除去少数异常的误差,模型的预测相对误差稳定在10%以内,对于6步提前预测来说,10%的误差是个可以接受的范围,如果将连续监测的天数增加,确保更多的数据量,不光可以提高模型的预测精度,如果数据足够,模型的每一步可以变为0.5 h或1 h,那样就可能在数小时前预知可能的藻类暴发,产生对“水华”现象精确预测的实际意义。
3 小结与讨论
通常我们对叶绿素a的预测都是建立在较长周期的数据基础上,得出一年中哪些月,哪些天藻类容易暴发,以至产生“水华”现象,这并不足以对藻类暴发起到预警作用。本实验通过连续监测的数据探讨在对叶绿素a在短周期内预测的可行性,并通过传统线性回归方法和人工神经网络分别建立同步和6步超前预测模型,结果显示,人工神经网络具有一定的优势,但要建立具有短期预警“水华”现象的有效模型,可能需要更多的数据,以及和“水华”现象发生的条件相关联。
[1] 罗固源,郑剑锋,许晓毅,等.次级河流回水区叶绿素 a与影响因子的多元分析:以临江河为例 [J].长江流域资源与环境,2009,18(10):964-968.
[2] 邓春光.三峡库富营养化研究 [M].北京:中国环境科学出版社,2007:14-35.
[3] 张晟,李崇明,郑炳辉,等.三峡库区次级河流营养状态及营养盐输出影响 [J].环境科学,2007,28(3):500-505.
[4] 纪晓亮,朱元励,梅琨,等.典型平原河网温瑞塘河地区的氮磷营养盐时空分布 [J].浙江农业科学,2012(11):1571-1574.
[5] 李贺,刘春光,樊娟,等.BP神经网络在河流叶绿素a浓度预测中的应用 [J].中国给水排水,2009,5(25):75-79.
[6] Oh H M,Ahn C Y,Lee J W ,et al.Community patterning and identification of predominant factors in algal bloom in Daechung Reservoir(Korea)using artificial neural networks[J].Ecol Model,2007,203:109 -118.
[7] 王蕾,杨敏,郭召海,等.密云水库变化规律初探 [J].中国给水排水,2006,22(13):45-48.
[8] 季洪杰,余淑花,李令春.对水库原水藻类的控制 [J].中国给水排水,23(6):49-51.
[9] 王飞儿,吕焕春,陈英旭,等.千岛湖叶绿素a浓度动态变化及其影响因素分析 [J].浙江大学学报:农业与生命科学版,2004,30(1):22-26.
[10] 浙江省水资源监测中心温州分中心.温瑞塘河水质评价报告 [R].温州:温州医学院,2006.
X 52
A
0528-9017(2013)04-0460-04
文献著录格式:李鹏程,纪晓亮,梅琨,等.水体中叶绿素a含量短周期预测的研究 [J].浙江农业科学,2013(4):460-463.
2013-02-05
浙江省科技厅重大专项 (2008C03009);温州市重大专项 (20082780125);温州市科技局对外科技合作交流项目 (H20100006)
李鹏程 (1987-)男,江苏泰州人,硕士研究生,主要从事GIS与环境科学研究工作。E-mail:lpc_0719@sina.cn。
张明华 (1955-),女,教授,博士生导师,主要从事环境生态领域研究工作。E-mail:mhzhang@ucdavis.edu。
(责任编辑:吴益伟)
