MATLAB在GPS定位坐标系统模拟中的应用

蒋全科，郭 娜

（1.成都理工大学,四川 成都 610059；2.成都理工大学 数学地质四川省重点实验室 管理科学学院，四川 成都 610059）

MATLAB在GPS定位坐标系统模拟中的应用

蒋全科1，郭 娜2

（1.成都理工大学,四川 成都 610059；2.成都理工大学 数学地质四川省重点实验室 管理科学学院，四川 成都 610059）

针对在GPS定位坐标系统中进行精密计算的复杂性，通过使用MATLAB来处理协议天球坐标系的定义及转换问题，以此来确定GPS卫星星座在天球坐标系中的具体位置。通过使用MATLAB来模拟其原理及计算过程，可大幅度提高GPS定位坐标系统中的计算速度以及精度。

MATLAB；GPS；坐标系统转换；协议天球坐标系

1 MATLAB概述

MATLAB是一种专业的数学软件，可用于算法开发、数据可视化、数据分析以及数值计算。MATLAB系统由MATLAB开发环境、MATLAB数学函数库、MATLAB语言、MATLAB图形处理系统和MATLAB应用程序接口（API）5大部分构成。 MATLAB 的应用范围非常广，包括信号和图像处理、通信、控制系统设计、测试和测量、财务建模和分析以及计算生物学等众多领域。附加的工具箱（单独提供的专用MATLAB 函数集）扩展了MATLAB 环境，以解决各种应用领域内特定类型的问题。此外，它独特的数学运算性能使MATLAB在工程数学计算和数值分析等领域有着绝对的优势，同时它又简单易学，具有面向对象的编程特点，编程效率高，是大多数工程师以及科学家在进行编程和科研时的不二之选。

2 MATLAB在协议天球坐标系的定义及转换中的应用

2.1 协议天球坐标系

天球坐标系是一种惯性坐标系，其坐标原点及各坐标轴指向在空间保持不变，而与地球自转并无关联，用于描述卫星运行的位置和状态。天球是指以地球质心M为中心、半径r为任意长的一个假想球体。我们研究的天球坐标系一般分为天球空间直角坐标系和天球球面坐标系2大类，在天球空间直角坐标系统中，天体s的坐标可以表示为（x,y,z），而在天球球面坐标系统中，天体s的坐标可以表示为(α,δ,γ)，因此有下列转换关系：

2.2 MATLAB模拟模型

首先确定 3 个参数 (α,δ,γ)，在球面坐标系中各参数的范围为0≤ α≤2π，0≤δ≤ π。在天球中，半径r任意，我们将其取为单位1，则有：

于是得到MATLAB模拟出的天球球体如图1所示。

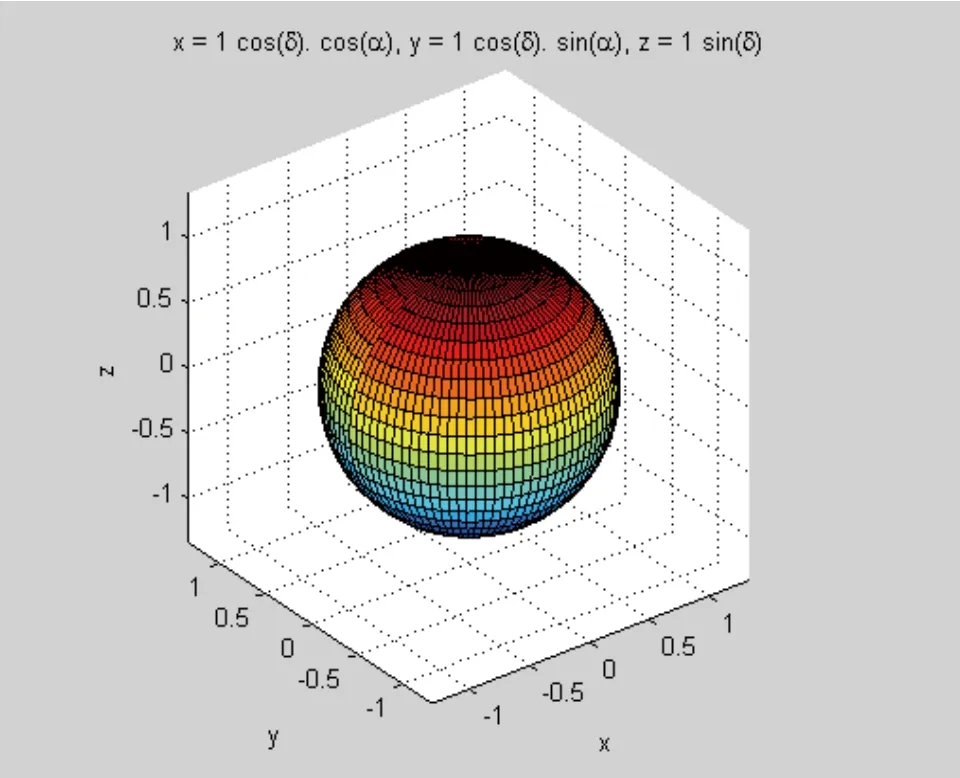
图1 天球球体模拟图

通过上述对天球的模拟可以看出，GPS卫星星座运行的轨道可以在这个球面坐标系内加以描述，这对GPS卫星星座的具体坐标定位有着决定性作用。

2.3 协议天球坐标系与瞬时平天球坐标系的转换

由于岁差和章动的影响，瞬时平天球坐标系的坐标轴指向不断变化，造成了一种非惯性坐标系统，因此不能根据牛顿力学定律来研究卫星的运动规律，需要通过数学物理模型来消除岁差和章动对坐标系的影响。由于章动影响极为复杂，涉及到多达106项的级数展开式，因此在这里我们只研究岁差变换模型。

协议天球坐标系与瞬时平天球坐标系的区别就在于岁差引起的坐标轴x指向不同。因此，只需要将坐标系加以旋转便可得到它们之间的转换关系。若取（x，y，z）CTS和（x，y，z）MT分别表示协议天球坐标系和瞬时平天球坐标系，则其转换关系为：

式中，z、θ、ζ分别为与岁差有关的3个旋转角，其表达式为:

式中，T=（t−t0）是从标准历元t0到观测历元t的儒略世纪数。

通过上述数学模型，运用MATLAB来研究2012年1月份的GPS卫星在天球中的坐标准确位置。从标准历元2000年1月15日TDB到2012年1月份所经历的儒略世纪数约为0.12世纪，设此时某一颗GPS卫星在协议天球坐标系下的坐标为 （x，y，m），想要求出卫星在消除岁差影响后瞬时平天球坐标系中的坐标，需要在MATLAB中进行如下操作：

打开MATLAB，输入edit，进行M文件的编辑，源程序如下：

因为研究的时点为2012年1月份，所以其他各变量均为定值，只需要输入卫星此时在天球坐标系中的坐标位置，便可消除岁差对卫星具体坐标的影响。

因此转换后的坐标为（9 960,10 027,10 031）。这就是在2012年1月份的这个时刻GPS某颗卫星在协议天球坐标系下的卫星坐标（10 000,10 000,10 000）在转换为瞬时平天球坐标系后的卫星的具体坐标。经过对GPS卫星星座在天球坐标系中定位的精密计算可知，岁差影响会对卫星在这个坐标点下的准确位置产生±0.13%～0.4%左右的误差。

3 结 语

运用MATLAB来处理GPS中协议天球坐标系的定义及转换，通过对这个过程的数学模拟，能够计算出复杂的岁差影响数学模型的准确值，并且计算出在（10 000,10 000,10 000）由于岁差的作用而对GPS卫星定位产生的误差值在±0.13%～0.4%。MATLAB进行复杂数学运算的能力非常强大，无论在GPS坐标转换、高程转换还是在整个测绘领域，都有很好的使用价值。

[1] 李天文.GPS原理及应用[M]. 第二版.北京：科学出版社，2010

[2] 张磊，毕靖，郭莲英.MATLAB实用教程[M].北京：人民邮电出版社,2005

[3] 邓中卫.GPS技术、应用与市场[M].北京：北京航空工业出版社,1996

[4] 魏子卿.GPS卫星测轨网研究[M].北京：北京星球地图出版社,1997

[5] 张凤举，王宝山.GPS定位技术[M].北京：北京煤炭工业出版社，1997

[6] 王广运.GPS测地研究与应用文集[M].北京：测绘出版社，1992

[7] 徐绍铨.GPS测量原理及应用 [M].武汉：武汉测绘科技大学出版社，1998

[8] 李延兴.GPS技术研究新进展[M].天津：天津科学技术出版社，1996

[9] 钱天爵,瞿学林.GPS全球定位系统及其应用[M].北京：北京海潮出版社，1993

[10] 洪大永.GPS全球定位系统技术及其应用[M].厦门：厦门大学出版社，1998

Application of MATLAB in GPS Positioning Coordinate System

byJIANG Quanke

According to the complexity of the precise calculation of the coordinate system of GPS positioning, this paper used MATLAB to process agreement celestial coordinate system definition and conversion, in order to determine the specific location of the GPS satellite constellation in the celestial coordinate system. Using MATLAB to simulate the principle and calculation process could greatly improve the computational speed and accuracy of GPS positioning in the coordinate system.

MATLAB, GPS, coordinate system conversion, Agreement Celestial Coordinate System

P228.41

B

1672-4623（2013）02-0071-03

10.11709/j.issn.1672-4623.2013.02.022

2012-05-07。

项目来源：国土资源部地质大调查资助项目 (1212010733803)；青藏专项资助项目(1212010818089)；西藏自治区矿产资源潜力评价资助项目(1212010813025)。

蒋全科，研究方向为国土资源信息化管理。