基于模拟退火粒子群优化的粒子滤波算法

江苏科技大学电子信息学院 刘 浩 杨官校 吴 将

1.引言

近年来，粒子滤波方法在国内外备受关注，与传统滤波方法相比，该方法具有简单易行，适用于非线性及非高斯噪声环境等优点，因而被广泛应用于视觉跟踪、机器人定位、航空导航、图象处理、故障检测、工业控制等诸多领域。[1-4]

粒子滤波(PF)的基本思想是先在状态空间中根据先验分布产生一组随机样本集合，这些样本被称为粒子，然后在观测的基础上，通过调节每一样本所对应权值的大小和样本的位置，来获得服从实际分布的样本，并以这些样本的均值作为系统状态估计值。

粒子滤波方法采用带有权重值的粒子集来近似表示后验概率分布，因此，理论上该方法可以表示任意形式的概率分布，然而，因为常规粒子滤波方法采用了次优的重要性函数，所以常规粒子滤波方法存在粒子贫乏和计算效率等缺点，为解决以上问题，国内外不少学者提出了改进方法。

Rudolph等[5]将UKF方法引入粒子滤波中，提出了无味粒子滤波算法(UPF)，其核心思想是利用UKF得到比常规PF更好的重要性函数，该方法将最新的观测值引入预测过程中，因此提高了常规粒子滤波的性能，但计算量也大大增加了；Clapp等[6]将模拟退火思想引入粒子滤波中，提出了模拟退火粒子滤波(SA-PF)，该算法引入退火重要性采样和中间分布的概念，改善了出现先验尾部观测值时的算法性能；方正等[7]提出了粒子群优化粒子滤波方法（PSO-PF），将粒子群优化算法引入粒子滤波方法中，利用粒子群(PSO)算法对PF的重要性采样进行优化将最新的观测值引入重要性采样分布中，使得重要性采样分布向后验概率较高的区域运动，提高了状态预估的精度，然而该方法仍然存在重采样过程带来的粒子缺乏多样性问题。

本文提出了基于模拟退火粒子群优化的粒子滤波算法(SAPSO-PF：Simulated Annealing Particle Swarm Optimized Particle Filter)，该方法基于一个高斯分布来不断更新粒子的速度，同时采用随机概率扰动的方式作为基本粒子群算法的全局极值更新条件，从而增加全局最优区域的搜索能力，避免了粒子过早的“趋同性”，使得粒子滤波的性能得到很大的提高。

2.基于模拟退火粒子群优化的粒子滤波算法

2.1 高斯粒子群优化粒子滤波

常规的粒子滤波采用了次优的重要性函数，因此，粒子的重要性采样过程是次优的。为了优化粒子滤波的采样过程，本文将粒子群优化算法融入粒子滤波中。

首先，将最新的观测值引入采样过程，并定义适应度函数为：

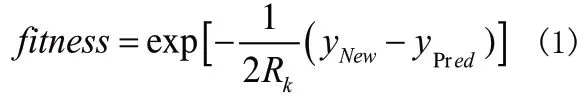
其中：Rk是观测噪声方差，yNew是最新的观测值，yPred是预测观测值。粒子群优化算法通过计算适应度值将所有的粒子向最优粒子移动。但有时经典的粒子群优化算法的最大速度等参数很难确定，因此本文采用一种改进的粒子群优化算法，即高斯粒子群优化算法(GPSO-PF：Gaussian Particle swarm Optimized Particle Filter)。

该方法基于一个高斯分布来不断更新粒子的速度，其收敛性好于经典的粒子群优化算法[7-8]。

如果粒子集都分布在真实状态附近，那么粒子群中每个粒子的适应度都很高。反之，如果粒子群中每个粒子的个体最优值以及粒子群的全局最优值都很低，则说明粒子没有分布在真实状态附近。此时粒子集利用粒子群优化算法，不断根据最优值并利用下式来更新每个粒子的速度与位置，使得粒子不断地向真实状态靠近：

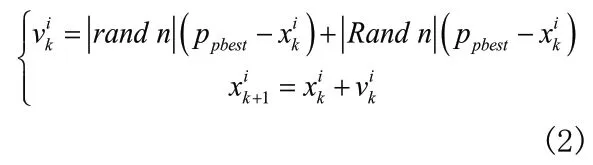
通过移动粒子群向最优粒子ppbest靠近，粒子群优化算法实质是驱动所有的粒子向高似然概率区域运动。当粒子群的最优值符合某阈值ε时，说明粒子群已经分布在真实状态附近，那么粒子群将停止优化。此时再对粒子集利用最新观测值通过下式进行权重更新并进行归一化处理：

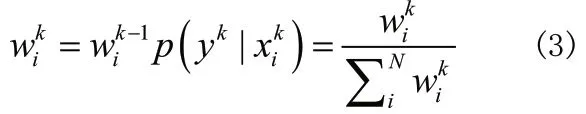
为了解决粒子滤波的退化问题，需要选择和复制权重值较大的粒子，即对粒子集进行重采样：

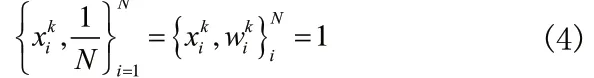
在重采样之后，真实状态附近的粒子权重值将会大。

通过以上的优化过程，使得粒子集在权重值更新前更加趋向于高似然区域，从而解决了粒子贫乏问题。同时，优化过程使得远离真实状态的粒子趋向于真实状态出现概率较大的区域，提高了每个粒子的作用效果。于是，粒子滤波需要大量粒子才能进行精确状态预估的问题也被削弱了，尤其当初始状态未知时。

2.2 模拟退火粒子群优化粒子滤波

粒子群算法的本质是利用本身信息、个体极值信息和全局极值三个信息，指导粒子下一步迭代位置。但是粒子群在追逐最优粒子过程中，随着它接近最优粒子，其速度越来越小，因此粒子群表现出强烈的“趋同性”，容易陷入局部极小点。本文引进模拟退火算法对其进行相应改进研究，得到模拟退火粒子群粒子滤波算法[9](SAPSO-PF)。

在粒子群算法中，粒子通过更新其全局最优和自身最优的方法来搜索全局最优解。但在其更新过程中，粒子只有遇到更好解的时候才会更新极值，这样做缩小了粒子的搜索邻域，使其很容易达到收敛，陷入局部最优。本文引进模拟退火算法对全局极值的更新条件做了改进，基本思想如下：

当新粒子的适应值大于当前全局极值时，系统一定接受该粒子；当新粒子适应度小于全局极值时，按式(5)计算出模拟退火概率p，当p大于阈值r的时候，r为(0，1)间的随机值，也接受该粒子，否则不接受。模拟退火概率计算如下：

式中Tt为第t次迭代的温度，Tt=Kt×Tt-1，K为降温系数；ΔD为当前粒子失真变化，ΔD=1f（Ni）-1pg，f(Ni)为第i个粒子的当前适应值，pg为当前全局最优适应值。

改进算法的全局极值更新条件采用了随机概率扰动接受的方式，既接收优化解，也可以接受恶化解，增大全局搜索范围。Tt很大时，使局部极值与全局极值之间的差值很大，接受概率比较大，可以接受的较差解比较多；Tt不是很高时，使差值小的状态易于接受，即中温时，易于接受与当前状态相比不是很差的解；Tt很小时，差值足够小的状态才易于接受，即低温时，只能接受与当前状态相比差很少的解。当经过足够长时间的温度下降过程，固体达到最小能量状态时，相应也达到了全局最优解。

2.3 模拟退火粒子群优化粒子滤波伪代码

Step1：取得量测值。

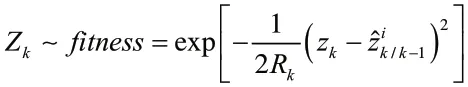
其中Zk为最新量测值，为预测量测值。

Step2：初始化，在k=0 时刻，从重要性函数采样取N个粒子，抽样出的粒子用表示。重要性密度函数取转移先验：

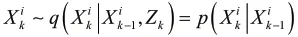
Step3：重要性权值计算。

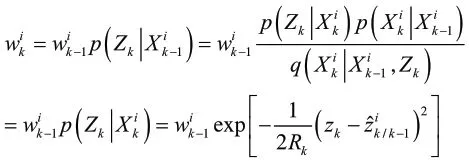
据最优值并利用下式来更新每个粒子的速度与位置，使得粒子不断地向真实状态靠近：

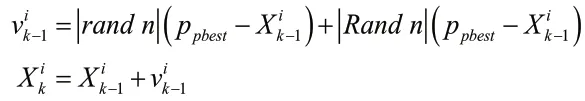
当新粒子的适应值大于当前全局极值时，系统一定接受该粒子；当新粒子适应度小于全局极值时，按计算出模拟退火概率p，当p大于阈值r的时候，r为(0，1)间的随机值，也接受该粒子，否则不接受。模拟退火概率计算如下：

式中Tt为第t次迭代的温度，，K为降温系数；ΔD为当前粒子失真变化，ΔD=1f（Ni）-1pg，f(Ni)为第i个粒子的当前适应值，pg为当前全局最优适应值。

通过移动粒子群向最优粒子ppbest靠近，粒子群优化算法实质是驱动所有的粒子向高似然概率区域运动。当粒子群的最优值符合某阈值ε时，说明粒子群已经分布在真实状态附近，那么粒子群将停止优化。此时再对粒子集利用最新观测值通过下式进行权重更新并进行归一化处理：

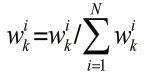
Step5：输出。

Step6：判断是否结束，若是则退出本算法，若否则返回step2。

3.实验仿真及分析

状态估计仿真模型选取如下：

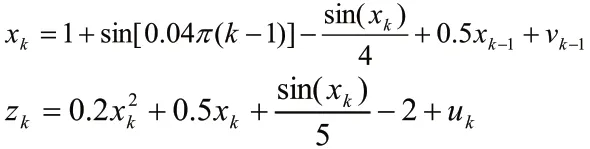
其中vk服从伽马分布ςa(3,2)，表示系统噪声，测量噪声uk服从高斯分布N(0,0.0001)。实验中使用的粒子数目为N=200个，观测时间为T＝60，进行100次独立实验。UT参数设置为α=1，β=0，κ=2。

表1 100次独立实验后不同非线性滤波算法产生的均方误差的均值与方差Table1 100 independent experiments of different non-linear filtering algorithm mean square error

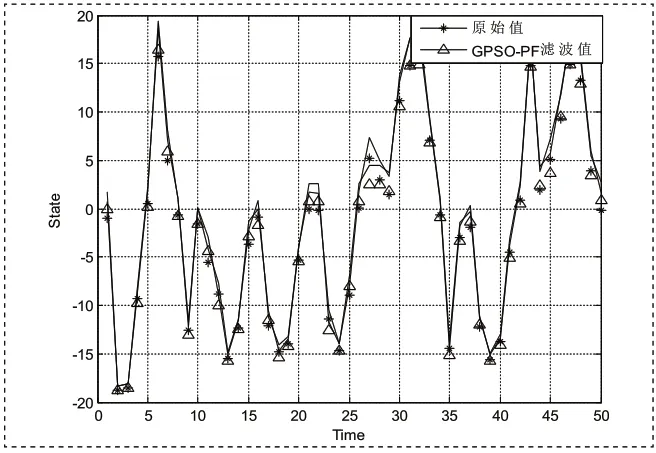
图1 高斯粒子群粒子滤波状态估计N＝100Fig 1 State estimation of Gaussian Particle swarm particle filter

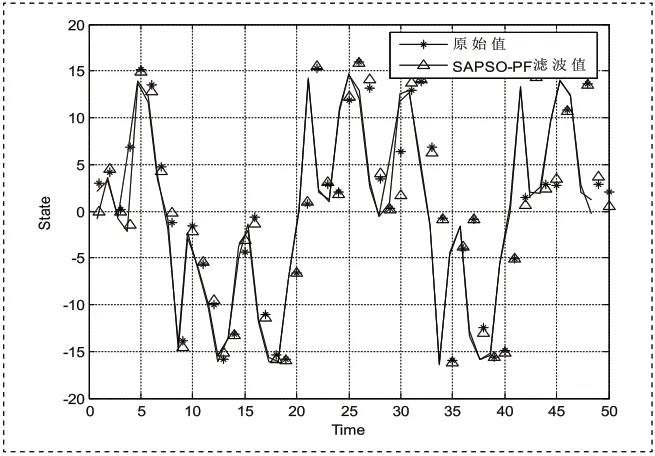
图2 模拟退火粒子群粒子滤波状态估计N＝100Fig2 State Estimation of Simulated Annealing Particle Swarm Optimized Particle filter

粒子群优化粒子滤波与其他非线性滤波算法估计性能比较表如表1所示。在几种粒子滤波器中，PF对于非线性系统的适应性是最差的。经过100次独立运行实验后，可以看到SAPSO-PF算法的误差和均值均为最小，其总体误差小于其它算法。具体状态估计曲线如图1和图2所示，同样可以看出SAPSO-PF算法得出的估计结果优于GPSO-PF算法。

4.结论

在利用常规粒子滤波方法进行系统状态预估时，通常粒子集数目不能太大，否则系统的实时性很差。另一方面，如果粒子集的数目太小，则系统的鲁棒性将会降低，容易受到粒子贫乏现象的影响。特别是在观测量较准确或似然概率位于先验概率尾部的情况下，常规粒子滤波器的预估性能很差。本文通过分析常规粒子滤波方法存在问题的原因，将粒子群优化算法同粒子滤波算法结合，得到高斯粒子群粒子滤波算法(GPSOPF)，使得采样分布向后验概率较高的区域运动，从而减轻了粒子贫乏现象的产生，同时提高了状态预估的精度，在此基础上还讨论了一种模拟退火粒子群粒子滤波算法(SAPSO-PF)，采用随机概率扰动的方式作为基本粒子群算法的全局极值更新条件，从而增加全局最优区域的搜索能力，在一定程度上提高了粒子滤波的有效样本数。

[1]Bog dan K.Finding location using a particle f ilter and histogram matching[C].Proc of Artif icial Intelligence and Soft Computing.Poland：Springer，2004：786-791.

[2]Guthrun S.Particle filters in robotics[C].Proc of Uncertainty in AI.San Francisco：Morgan Hofmann Publishers，2002：511-518.

[3]张瑞华，雷敏.粒子滤波技术的发展现状综述[J].噪声与振动控制，2010，4(2)：1-4.

[4]陈志敏，薄煜明，吴盘龙等.基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J].2013，28(2)：193-200.

[5]Van M R，Doucet A.The unscented particle filter[R].Cambridge：Cambridge University，2000.

[6]Cl app T C.Statistical methods for the processing of communication data[D].Cambridge：University of Cambridge，2000.

[7]方正，佟国峰，徐心和.粒子群优化粒子滤波方法[J].控制与决策，2007，22(3)：273-277.

[8]Rockling R A.Gaussian swarm：A novel particle swarm optimization algorithm[C].Proc of the IEEE Conf on Cybernetics and Intelligent Systems.Singapore，2004：372-376.

[9]高鹰，叶胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用，2004，40(1)：47-50.

[10]黄文娟，马勤，王立群，杨淑莹.一种粒子群优化扩展卡尔曼粒子滤波算法[J].天津理工大学学报，2009，25(5)：51-53.