时间序列分析法在延吉市地下水动态预测的应用

李勇海

延吉市国土资源局，吉林 延吉 133000

地下水动态受一系列自然和人为因素的影响,它是地下水系统受多种输入所激励而产生的综合效益。降水、用水等因素可视为系统的的输入, 地下水位可视为系统的输出。由于年内的降水、蒸发、用水等具有一定的规律性, 地下水位在年内的变化也有一定的规律性。，而这些因素表现了一定的趋势性、周期性和随机性,基于此, 本文选取了时间序列分析方法对该区的地下水动态进行预测分析,并用实例进行了验证。

1 时间序列模型的原理

1.1 模型的基本组成

水位动态序列H（t）是由趋势成分T（t）、近似周期成分P（t）和平稳随机成分R（t）组成的。建立模型的过程是从已知序列（观测值）H（t=1,2,3,∧,n）中依次提取各分量的过程。一旦建立了各分量的数学模型后,再将其线性叠加,就得到了地下水水位预测模型,其表达式为[1]∶

1.2 地下水水位埋深时间序列模型各分量的确定

1.2.1 趋势分量的确定

对于趋势分量T（t）可用多项式逼近,即∶

可采用多元回归方法确定待定系数C012,…,Ck和阶数k。为检验拟合结果需在一定的显著性水平下计算趋势曲线拟合的相关系数R，R越接近1,表明T（t）与tk（k=1,2,…,K）的线性关系越密切，对给定信度及不同的自由度,可以求出R的临界。值（查表）,只有当R值大于相应临界值时,回归方程才有实用意义。若无最佳拟合函数则认为无趋势项或趋势项不显著。

1.2.2 周期分量的确定

趋势函数确定后再对扣除趋势分量后的部分进行周期项分析[2]，即：

采用谐波分析方法进行周期分量的分析提取，对序列Y（t）可用L个波叠加的形式表示其估计值为：

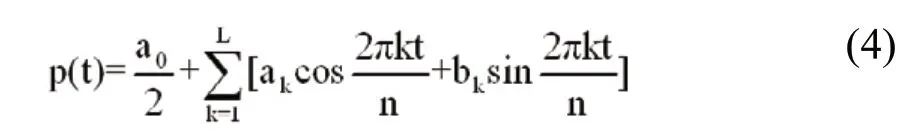
式中L为谐波个数,一般取n/2 的整数部分；k通常称为波数, 一般认为L个分波各有n/1,n/2,∧∧,n/k的周期,即第k个分波的频率为k/n；ak,bk为傅立叶系数,其计算式为∶

由此可求得a0,ak,bk，为节省工作量通常在L个波中选取波动比较显著的几个谐波相加来估计Y（t），在实际应用中只需选取前6 个显著谐波就能满足精度要求。

1.2.3 随机分量的确定

消除了趋势分量和周期分量后得到随机分量时间序列设为X（t），即：

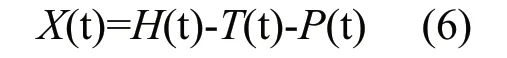
X（t）为一般为平稳随机系列，可使用自回归模型AR来拟合，X（t）均值一般为0，设R（t）为X（t）的估计值，则其自回归模型为：

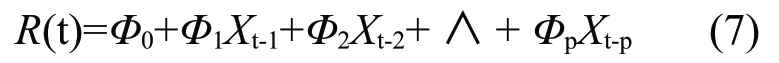
式中p为模型阶数；Φi为模型自回归系数,i=（0,1,2……p）。对某一阶数的自回归模型,类似多元回归计算可求得自回归系数Φi。

模型阶数的确定本文采用了AIC准则[3]。

1.2.4 精度检验

将上述趋势分量、周期分量、随机分量线性叠加,即可得到地下水位的总预测模型，对于用模型作出的地下水动态预报,其精度可采用后验差法进行检验。预报精度评价标准见表1。对模型进行精度检验预报精度评价可按表1.1 所列标准考虑。

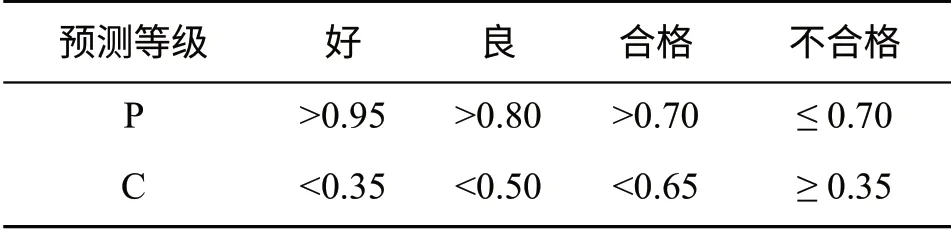
表1 预报精度评价标准表Table 1 Prediction accuracy evaluation standard

如果P,C值都在允许范围内,则模型可用于计算预报值,否则需要对模型进行检查、分析和重新调参。模型合格后,还要随机模拟足够长的序列,采用短系列法和长系列法判定模型的实用性[4]。

2 延吉市地下水动态预测

本次研究在研究区选择了多个具有代表性的地下水位长期观测井进行分析预报，现仅以Y042 号井为例，对该井2008 至2012 年月平均水位资料进行分析，建立地下水位动态时间序列模型，并对模型进行分析。

2.1 模型参数的识别

首先依据上述公式，计算得到该观测井的趋势项系数和相关系数如下：

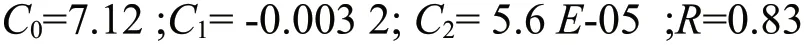
对剔除了趋势项之后的水位埋深时间序列提取周期项。计算傅氏系数列于表2。

对经过趋势项周期项提取过后的残差做自回归模型识别，其结果列于表3。

将趋势分量、周期分量和随机分量叠加即得到地下水水位埋深预测模型即∶

表2 傅氏系数计算结果Table 2 Fourier coefficient computing result

表3 自回归系数计算结果Table 3 Autoregressive coefficient computing result

2.2 精度检验

地下水动态时序模型建立后需对其精度进行检验，本次采用2007 年数据进行后验预测检验。其后验预测结果表4 及图1。

首先进行后验差计算，检验所建立的地下水埋深时间序列模型的后验差比值C和小误差频率P分别为0.245 846 和1。

从图1 及表4 中可以看出其拟合精度较高。其最大绝对误差仅为0.152，最小达到了0.025,相对误差均小于2.5%，满足精度要求故该模型可应用于预报未来地下水水位埋深。

2.3 模型预报

在进行实际预报前需要进行反复调参直至满足精度要求，现依据经过精度检验了的预报方程预报该井2016 年各月地下水位埋深水位埋深预报值和曲线，其结果分别见表5 和图2。

表4 后验预测误差计算表Table 4 Posterior predictive error calculation

图1 后验预测拟合曲线（Y042）Fig.1 Posterior predictive f itting curves (Y042)

3 动态预报分析

通过上述计算可知，运用时间序列分析方法所建立的研究区地下水位时间序列模型能较全面地反映延吉市地下水位动态的变化规律, 如地下水位变化所具有的趋势性、周期性及其受各种无规律干扰因素影响下的地下水位的随机波动等。

（1）对趋势项的分析可知该地区的地下水水位埋深各地区以下降为主，这主要是由于各地区补给量均小于排泄量造成的，尤其是在超采严重地区地下水位下降幅度愈来愈大，出现降落漏斗面积也不断增大。因此，必须对该区地下水开采利用进行严格控制和科学管理，防止地下水位继续下降而导致该区生态环境恶化。

（2）通过周期项分析可知该区地下水位动态具有两个主要的周期，一个周期长度为1 年，反映了1 年内源汇项的季节性周期变化，另一个周期长度为3 年，反映了多年内源汇项的季节性周期变化，主要揭示了该地区气候变化规律及特征。

表5 2016年Y042号井逐月预报水位埋深值Table 5 Monthly forecast water depth value of Well Y042 in 2016 m

图2 2016年预报水位埋深曲线（Y042）Fig.2 Forecast water depth curve in 2016 (Y042)

4 结论与建议

（1）运用时间序列分析方法建立了延吉市地下水埋深预测模型，结果表明拟合精度和预测精度均较高，该模型较全面地反映了地下水位动态变化规律且计算简单，所需资料较少且易于获得，是一种较好的模拟预测模型，能很好地应用于分析地下水位动态的趋势性和周期性以及进行地下水埋深预测为延吉市地下水的合理开发利用及水资源规划提供可靠依据。

（2）但是，由于这类模型没有反映地下水流动系统的动力学机制，从而没有表示出系统各要素之间的动力学关系。因此用时间序列分析建立的模型在应用上受到了很大限制，如何发挥随机数学方法和确定性数学方法各自的优点建立既能反映地下水流动系统中不确定性影响因素又能刻划其动力学机制的随机确定性模型将是今后时间序列分析方法的主要研究内容，也将使时间序列模型的应用前景更加广阔。

[1] 陆洪波.北京市区浅层地下水位预测预报[J].工程勘察,1997,(1):36-41.

[2] 李 平,卢文喜,杨忠平.频谱分析法在吉林西部地下水动态预报中的应用[J].水文地质工程地质,2005,(4):70-73.

[3] 黄忠恕.波谱分析方法及其在水文气象中的应用[M].北京气象出版社,1983.

[4] 杨金忠,蔡树英.地下水动态预报的多层递阶组合模型[J].水科学进展,1995.6(2):100-106.