石墨炉原子吸收法测定土壤中痕量金的不确定度的评定

关逸考，赵东阳

吉林省有色金属地质勘查局六○八队 ,吉林 长春130507

测量不确定度表征合理地被赋予被测量之值的分散性，是与测量结果相关联的参数。我国在1999 年实施了的《测量不确定度评定与表示》（JJF1059—1999）[1]计量技术规范，由此测量不确定度评定成为中国实验室通过国家认可委员会认可条件的必要条件之一。本文依据《地质实验室化验测试管理规范》[2]的要求，针对石墨炉原子吸收法测定土壤中痕量金的测定，对其测量不确定度进行了系统的分析与评定，并给出相应的结果表示。

1 测定方法[3]

称取10.00 g 样品于坩埚中，置于箱式电炉内，于650 ℃焙烧1 h，取下冷却，将样品移入250 mL聚乙烯瓶中，加王水30 mL 王水（1：1）、10%三氯化铁溶液4 mL，拧紧瓶盖。于水浴箱中加热溶解1 h。冷却后取下瓶盖，加水80 mL 左右，放入一块聚醚型泡沫塑料，用玻璃棒挤压泡沫塑料和液体充分接触后再盖上瓶盖。于振荡器上振荡45 min。取出泡沫型塑料，用蒸馏水洗净，并挤干。放入25 mL 比色管中，加入1%的硫脲溶液5 mL，于沸水浴上解脱15 min，取下用玻璃棒挤压泡沫40 次左右，将溶液倒入10 mL 烧杯中， 于Z-2700 型石墨炉原子吸收分光光度计测定金的质量分数。

2 数学模型

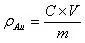
式中：ρAu—试样中金金质量分数（ng/g）；

C—从标准工作曲线上查得试液金的质量浓度（ng/mL）；M—称取试样的质量（g）；

V—解脱时所用硫脲的体积（mL）；

3 不确定度的来源识别

影响岩石中金的含量主要有测量重复性的不确定度；试样质量的不确定度；解脱时硫脲体积的不确定度；标准溶液的配制的不确定度；标准曲线产生的不确定度。

4 不确定度分量的计算

4.1 测量重复性的不确定度

对于某一标准物质进行10 次的重复测定，测定结果见表1。单次测量标准差：s=0.59，平均值标准偏差：； 相对标准不确定度urel（ref）=0.19 /10.38 =0.018。

4.2 称取样品质量（m）的不确定度

天平只考虑校准和分辨力所带来的不确定度，按照《电子天平检定规程》[4]JJG1036-2008 的规定，此类天平的允许误差为0.1 g，按均匀分布，其标准不确定度称取质量为10.00 g，则相对标准不确定度为：urel（m）=0.082 g/10.00 g=0.008 2。

4.3 解脱时硫脲体积的不确定度

加入萃取溶液用的是50 mL 滴定管，按照JJG196-2006《常用玻璃量器》[5]规定，50 mLA 级滴定管的允差为±0.05 mL，按均匀分布得；重复性：已经合并至试样测量的重复性中，故不再重复评定；温度：水的膨胀系数为2.1×10-4mL/℃-1，实验室温度变化为3 ℃，则体积变化为±50×2.1×10-4℃-1×3 ℃=0.0315 mL，计算标准不确定度时温度变化按均匀分布计算。两项合成得50 mL 滴定管标准不确定度为其相对不确定度为urel（V）=0.034 2 mL /50 mL=0.000 68。

表1 试样的重复性测定Table 1 Repeatability determination of sample

4.4 标准溶液的不确定度

吸取1 000μg/mL 金标准储备液1 mL 于1 000 mL 容量瓶中，加酸稀释成1 000 ng/mL 金标准溶液，然后配制成标准系列溶液。

4.4.1 金标准贮备液的不确定度

金标准贮备液是由国家标准物质中心提供，浓度为1 000μg/mL，证书给出其相对不确定度为0.3%， 按均匀分布，其相对标准不确定度为u（c0）rel=0.3%/k=0.001 73。

4.4.2 稀释过程中引入的不确定度

1 mL 单标线移液管（A 级）可以忽略。这里只考虑1 000 mL 容量瓶（A 级）不确定度。1 000 mL 容量瓶允许误差为±0.4 mL，按均匀分布得；重复性：对典型的1 000 mL 容量瓶充满液体至刻度的变动性实验得出0.10 mL，可以直接用作标准不确定度；温度：水的膨胀系数为2.1×10-4mL/℃-1，实验室温度变化为3 ℃，则体积变化为±1 000×2.1×10-4℃-1×3 ℃=0.63 mL，计算标准不确定度时温度变化按均匀分布计算。三项合成得到标准不确定度：u（V1 000）=0.442 mL，相对不确定度为urel（V1 000）= 0.442 mL /1 000 mL =0.000 442。

则由标准溶液引起的相对不确定度为∶

4.5 标准曲线引起的不确定度

吸 取0,0.5,1.0,2.0,3.0,mL 1 000 ng/mL 金 标准溶液于100 mL 容量瓶中，配制成浓度为0,5.0,10.0,20.0,30.0 ng/mL 金的工作曲线，每个溶液重复测定3 次，以金的质量浓度为横坐标坐标，吸光度为纵坐标，进行线性拟合，其数学模型为A=b×C+a。所得的吸光度响应值见下表2。由最小二乘法可求出线性方程为A=0.002 1C+0.000 234（b=0.002 1；a=0.000 234），相关系数r=0.999 2。回归曲线的标准方差SA/ρ（由回归曲线计算出的A值与实际测得Ai值之差）按贝塞尔公式求出∶,n-2=3×5-2=13 求得：SA/ρ=0.000 95，对于本次测量，试样的预估值C估=20.76 ng/mL，试样平行测量两次，p=2，则拟合标准曲线的不确定度可按下式计算：

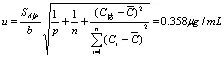
表2 标准溶液度及其响应值Table 2 Standard solution ratio and the response value

表3 不确定度分量Table 3 Uncertainty components

5 合成标准不确定度

所得的各个分量不确定度见表3。

将各项不确定度分量合成得相对标准不确定度：

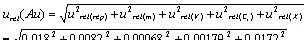
则 标 准 不 确 定 度 为u（Au）=0.026×10.38 ng/g=0.27 ng/g

6 扩展不确定度

取包含因子k=2，得到扩展不确定度Urel=0.27 ng/g×2=0.54 ng/g。

7 测定结果表示

本次测量金的质量分数用不确定度可表示为：10.38±0.54μg/g，k=2。

8 结语

经过对不确定度各分量的评定可以看出，重复性和标准曲线最终合成不确定度贡献比较大，因此在分析过程中减少样品的损失率、提高标准曲线灵敏度是降低不确定度的重要途径。

[1] JJF1059—1999,测量不确定度评定与表示[S].

[2] DZ/T0130—2006,地质实验室测试质量管理规范[S].

[3] 胡 明，关逸考.黄金-石墨炉原子吸收法测定化探样品中痕量金研究[R]. 长春，长春黄金研究院,2006.

[4] JJG1036-2008,电子天平检定规程[S].

[5] JJG196-2006,常用玻璃量器[S].