航道尺度对波高分布的影响
2013-01-21林尚飞陈国平严士常陈小婷
林尚飞,陈国平,严士常,陈小婷
(河海大学港口海岸与近海工程学院,海岸灾害及防护教育部重点实验室,江苏 南京 210098)
在波浪向岸传播过程中,由于地形的变化和各建筑物的影响,会产生浅化、折射、波能耗散绕射等现象。在海港建设中,常常需要通过开挖港池与进港航道以达到使用的要求,这也对波浪传播产生一定的影响。
关于航道对波浪的折射作用,目前已有不少的研究。早在上世纪70年代,JA Zwamborn和G Greve[1]在南非理查德港航道竣深物理模型实验中发现进港航道使波浪发散和会聚的问题,并提出了“临界入射角”的概念。在1987年烟台港西港池二期工程[2]以及1991年大连港大窑湾散粮码头工程[3]中又发现航道对波浪有较强的作用。此后,赵智帮[4]针对上述工程,探讨了航道对波浪的发散作用以及波能在某一区域的集中现象。另外,诸多学者通过建立数学模型,探讨航道对波浪传播的影响。例如,李玉成[5]采用不规则波的缓坡方程研究了航道的折射作用,探讨通过合理的航道开挖方式改变防波堤前波浪异常叠加现象。左其华、杨正己[6]应用抛物线型波浪折、绕射联合计算波浪数学模型研究航道对波浪传播的影响。吴达开[7]将透浪侧界抛物线模型结合方向谱计算,研究黄骅港一期工程中航道对波浪影响问题。还有的学者[8-13]基于Boussinesq方程对航道开挖后波浪的传播进行了数值模拟研究。诸多研究表明,当波浪遇到航道时,其传播规律会因为航道的存在而发生变化,而航道的尺度与波浪的折射有着密切的关系。由于数学模型对于各种物理过程有很多假设,而且物理模型相对于数学模型更为直观,因此本文基于物理模型试验结合工程实例来研究航道尺度对波浪传播的影响规律。
1 试验概况
1.1 工程概况
本试验为揭阳港靖海作业区通用码头工程整体波浪物理模型,工程拟建3个通用泊位,其中包括1号10万吨级泊位,2号5万吨级泊位和3号5 000吨级泊位,并配套散货专用堆场。港区进港航道等级为15万t,航道底高程-19.4 m,设计底宽214 m。工程地处广东省东南部,位于靖海湾内侧,工程总平面布置图见图1。
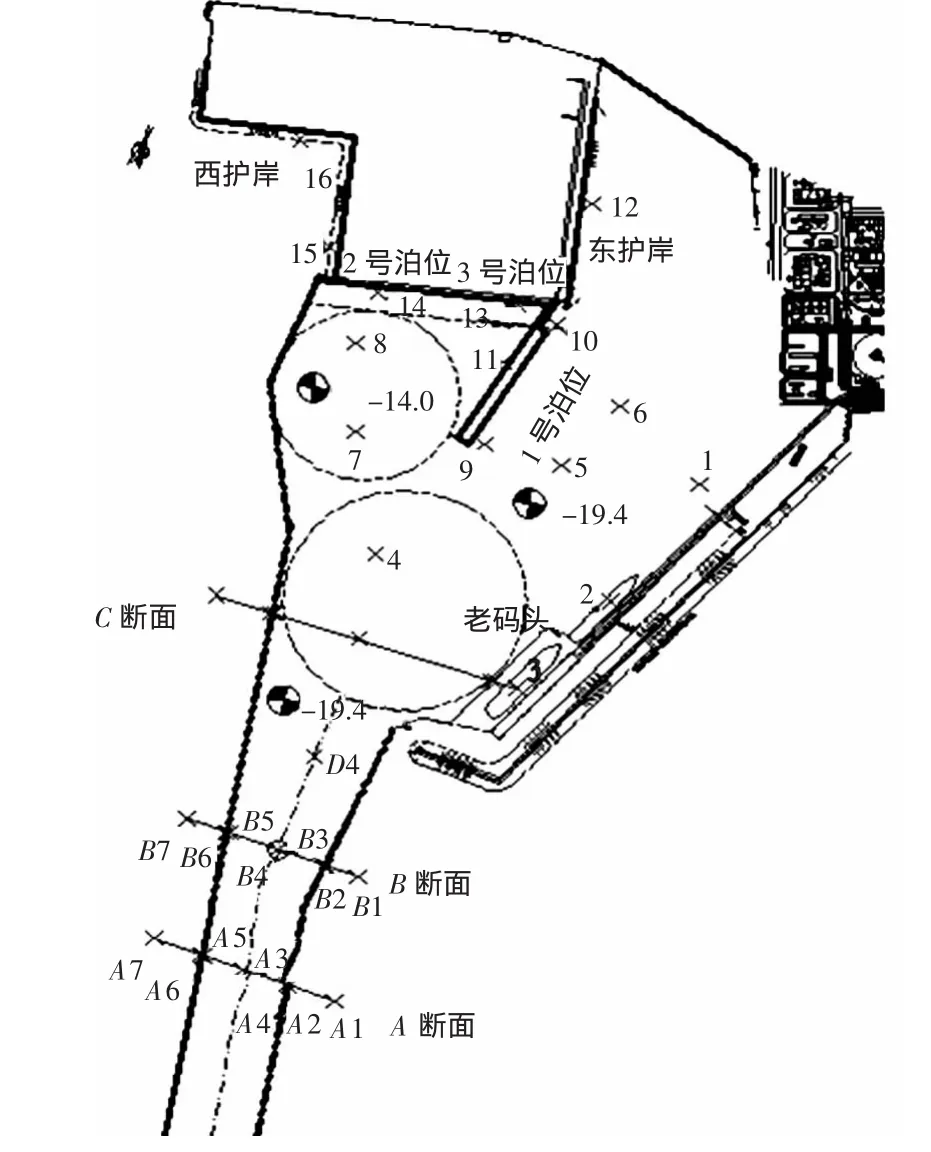
图1 工程平面布置图(15万t等级航道)
1.2 物理模型简介
波浪整体物理模型试验遵循JTJ/T 234—2001《波浪模型试验规程》,模型按重力相似准则设计,为定床、正态模型。综合考虑试验水池、模型范围、波浪要素以及试验仪器测量精度等因素,确定模型几何比尺为1∶100。试验在80 m×40 m×1.2 m的大型波浪水池中进行,水池中装备有多向不规则波造波机系统,可模拟规则波和各种谱型的不规则波。为了减小港池边壁的波浪反射影响,模型外围边界设置了消浪设施。码头沉箱及引桥采用有机玻璃按设计图纸模拟制作。试验中各测点波高采用DJ-800型多功能数据采集、处理及分析。模型中15万t等级航道试验测点布置见图1。在进港航道口门附近A、B、C断面布置三排波高仪,每排7个,分别位于航道轴线、边坡坡底、边坡坡顶和边坡距离300 m处,其中B4测点为试验中波浪要素率定点。港内区域在回旋水域及各建筑物前沿位置放置波高仪。
在15万t等级航道试验后,开展了进港航道等级为10万t(航道底高程-15.5 m,设计底宽200 m) 和5万t(航道底高程-14 m,设计底宽160 m)的整体波浪试验,以研究航道尺度对波浪传播的影响。在不同等级的航道试验中,工程平面布置不变,且根据工程地质勘探资料,航道区域土质类型为中风化或微风化花岗岩,因此航道的边坡不变且均为1∶1,测点位置布置原则与图1中相同,仅改变航道宽度和航道港池底高程。试验采用波要素为数学模型计算提供(见表1)。
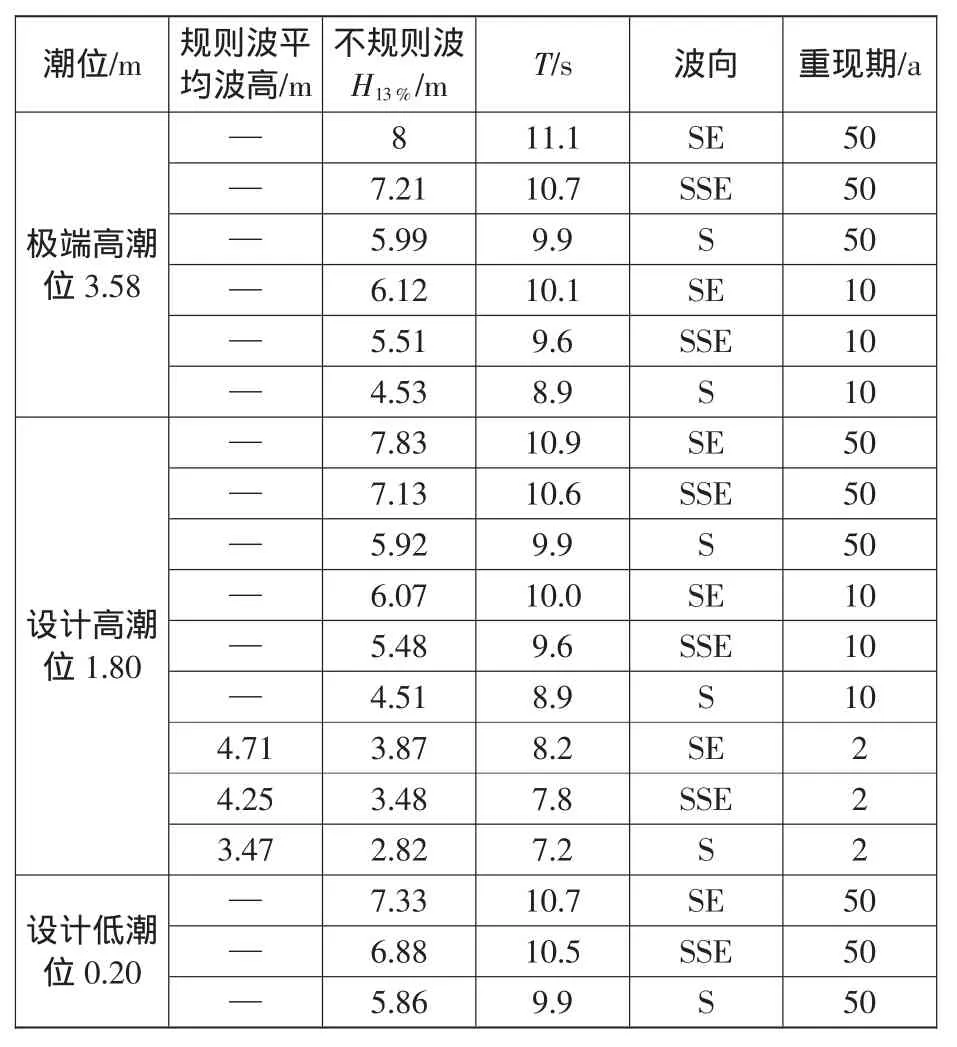
表1 特征点设计波浪要素
2 试验结果分析
本试验可分为4部分,包括原始地形和3个不同等级航道开挖条件下各测点波浪特征试验。由于在相同条件下,波浪重现期为50 a一遇、10 a一遇和2 a一遇的不规则波对波浪的传播影响类似,因此本文主要选择10 a一遇的不规则波进行分析。
2.1 波浪入射角的影响
2.1.1 航道内波能变化
波向线与航道轴线间的夹角称为波浪入射角,本文中以α表示。航道对波浪作用,波浪入射角的影响很大,能够显著改变航道区域的波浪传播,使得港内波高分布明显不同。在SE向波浪入射时,波浪入射角38°,SSE向波浪入射时,波浪入射角为15.5°,S向波浪入射时,波浪入射角为7°。
波浪传播至进港航道区域后,波能进入航道内的途径有两种,一是外海波浪从航道始端直接进入航道内,这部分波能可称为直接入射波能;二是波浪从航道边坡上入射,这部分波能可称为侧向入射波能。当波浪以小角度入射时,直接入射波能对航道内波高起主导作用;当波浪入射角较大时,侧向入射波能起主导作用。图2、图3分别表示在15万t等级航道和10万t等级航道试验中极端高水位10 a一遇不同波浪入射角条件下航道轴线各测点比波高分布。图中横坐标以A4测点位置为原点,纵坐标为比波高值。当波浪入射角<10°时,波浪能量基本沿着航道轴线射,随着波浪的传播,由于航道内外水深差异,波浪在航道边坡上向浅水方向发生折射,能量向航道外侧扩散,因此沿着航道轴线上的比波高逐渐减小。随着波浪入射角的不断增大,侧向入射波能增多,航道轴线沿程比波高在一定范围内呈现增大的趋势。
从图中可以看出,当波浪入射角为7°和15.5°时,航道轴线各点比波高值大多小于1,而当波浪入射角为38°时,航道轴线出现较大范围的比波高值大于1。因此,在不同的波浪入射角中存在某一临界角使得航道内比波高值大于1,即航道内波能较为集中,波高增大。JA Zwamborn和G Greve的研究验证了临界入射角的存在。他们的研究表明在波浪小角度入射时,波能向航道两侧扩散,而在入射角很大时,波浪可以穿越航道,波浪传播受到航道的影响很小,在二者之间存在临界入射角,使得波浪在航道内会聚,航道内波高增大。
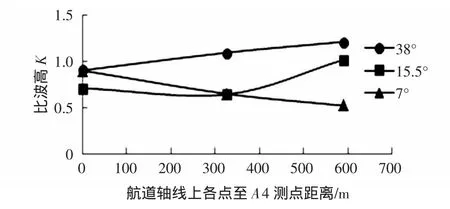
图2 15万t等级航道试验航道轴线比波高
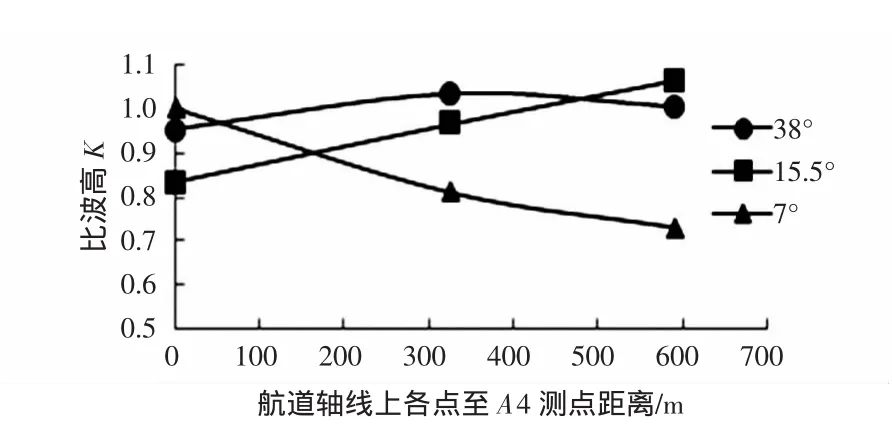
图3 10万t等级航道试验航道轴线比波高
2.1.2 坡肩上波能集聚
在各等级的航道试验中,进港航道口门前断面比波高分布呈现单向偏盆状态(见图4)。图4表示在15万t等级航道试验中,极端高水位(航道内水深为23.0m)波浪重现期为10 a条件下,A断面比波高的分布。图中以航道轴线为横坐标原点,西侧为横坐标负方向,东侧为横坐标正方向。SE、SSE向波浪入射时,航道东侧为迎浪侧,西侧为背浪侧;S向入射时则相反。当S向波浪入射时,入射角度较小,航道内传播波浪在航道边坡处向外折射,在航道迎浪侧与背浪侧比波高值相差不大,且两侧比波高值均大于1。当波浪入射角增大时,波浪传播至航道边坡时与航道内折射出的波浪相互叠加,波能在迎浪侧产生明显集聚现象,迎浪侧比波高值大于1,而背浪侧比波高值小于1,航道迎浪侧比波高值较背浪侧大约30%以上。
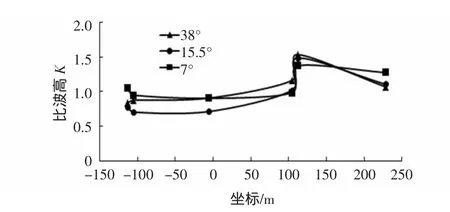
图4 15万t等级航道A断面比波高
上述分析表明当波浪以一定角度入射时,航道对波浪的影响体现在航道两侧的不等现象,在同一水深位置迎浪侧波高明显大于背浪侧。随着波浪入射角的增大,波浪直接进入航道的波能不断减少,而在航道迎浪侧边坡上波浪折射进入航道的波能增加,因此穿越航道到达航道背浪侧的波浪能量越多。在15万t等级航道试验中,设计高水位(航道内水深为21.2 m)波浪重现期为10 a条件下,波浪入射角为38°时,迎浪侧和背浪侧的波高都明显大于波浪入射角为15.5°的情况(见表2)。
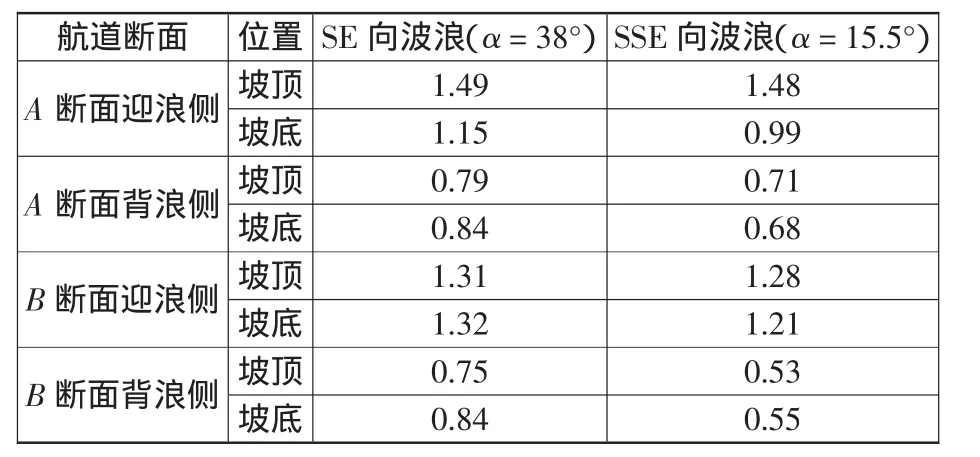
表2 航道两侧比波高
2.1.3 最大比波高值
在每组试验工况中,各测点中存在比波高最大值Kmax,为了探讨波浪入射角α与全场最大比波高Kmax之间的关系,选择15万t等级航道波浪重现期为50年的不同水位试验工况分析(见图5)。在同一水位条件下,波浪入射角α较小时,Kmax与α成正比,但是当α增大到一定程度,Kmax随着α增大反而减小。因此,存在某一入射角使得Kmax取得最大值。在不同入射角情况下,出现最大比波高的位置多位于航道口门附近,因此港口工程规划中应注意进港航道口门附近局部出现较大波高的情况。
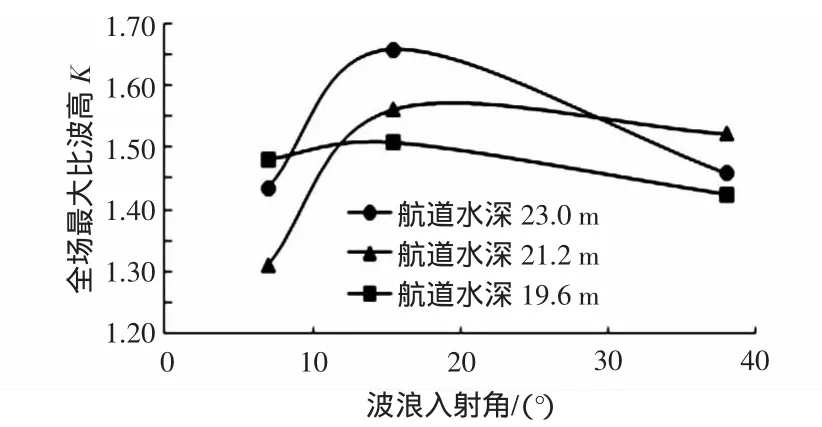
图5 全场最大比波高与入射角关系
2.1.4 港内波高
由于进港航道使得波浪的传播发生了变形,因此港内区域的波高必然发生变化,对于不同的波浪入射角,港内区域的波高分布特征也必然不同。选择15万t等级航道极端高水位波浪重现期为10 a的试验工况分析(见图6)。图6中横坐标为测点编号(相应测点编号见图1),纵坐标为比波高值。比波高K大于1表明测点波高较原始地形条件下有所增大,比波高K小于1则相反。从图中可以看出,不同入射角情况下老码头处的波高都增大;S向波浪入射时,除靠近口门附近的回旋水域及老码头波高增大外,其余各点波高均减小。SE向及SSE向波浪入射时,港内多数区域波高有所增大。当波浪以小角度入射时,波浪在航道内传播过程中向两侧发散,使得进入港内的波能减少,但是航道侧向位置老码头附近的波高就会有所增大。而波浪入射角增大时,波浪在航道迎浪侧边坡上折射进入航道的波能增加,进入港内区域的波能增加,因此港内多数区域比波高大于1。此外,波浪入射角α=15.5°情况下比α=38°时,港内区域的波高增大更为明显。同样说明了存在临界入射角使得传播至航道内的波能最大,即进入港内的波能最大,导致港内泊稳条件恶化。因此在工程实践中应合理选择航道走向,尽量避免强浪向及常浪向波浪以临界入射角进入航道。临界入射角可以采用下列公式估算[14]。
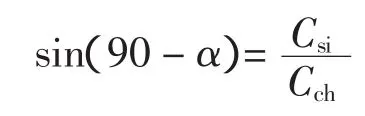
式中:α为临界入射角;Csi为航道外波浪波速;Cch为航道内波浪波速。
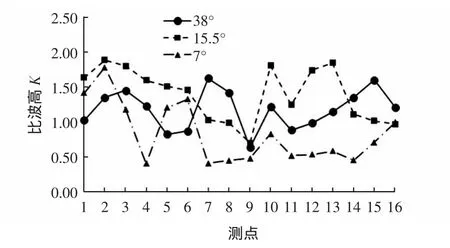
图6 港内比波高
2.2 航道水深的影响
航道水深变化有两种方式,一是航道的开挖,二是涨落潮,即水位的变化。对于航道某一固定断面,水深的变化体现在航道内外水深差与航道内水深之比(Δd/d内) 的变化。
在15万t等级航道试验中,先考虑波浪重现期50 a一遇SSE向波浪的情况下,探讨水位的变化对波浪迎浪侧波高的影响(见图7)。图7中从极端高水位到设计高水位,航道内水深降低,航道迎浪侧各测点波高增大。说明随着Δd/d内增大,航道的折射作用加强,被折射出航道的波能增加。但是在设计低水位的情况下,比波高反而有所降低,这是因为在设计低水位情况下试验水深较低,波浪破碎较为严重,因此各测点测量波高值偏小,使得比波高值较小。
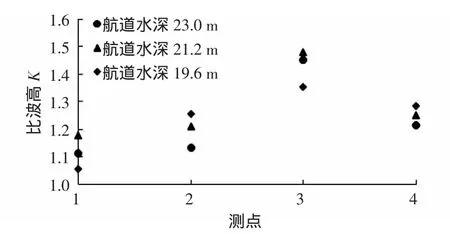
图7 航道迎浪侧比波高
上述分析表明,在波浪入射角较大时,航道迎浪侧的波高与Δd/d内呈现正相关的关系。对于波浪小角度入射的情况,选择15万t等级航道试验波浪重现期10 a一遇的S向波浪,改变水位探讨航道水深的影响。图8、图9和图10分别给出了不同水位条件下航道轴线、A断面以及港内比波高分布。随着水位降低,Δd/d内增大,波浪在航道边坡的折射更为显著。波浪小角度入射时,波浪向航道外扩散的波能增多,航道内波高减小,而航道外波高有所增大。图8中航道轴线上波高减小3.3%~19%。图9中A断面航道外波高增大约8%,航道内波高减小约5%。水位降低后航道内波能有所减少,即传播至港内区域的波能减少,使得港内区域多数测点波高降低。
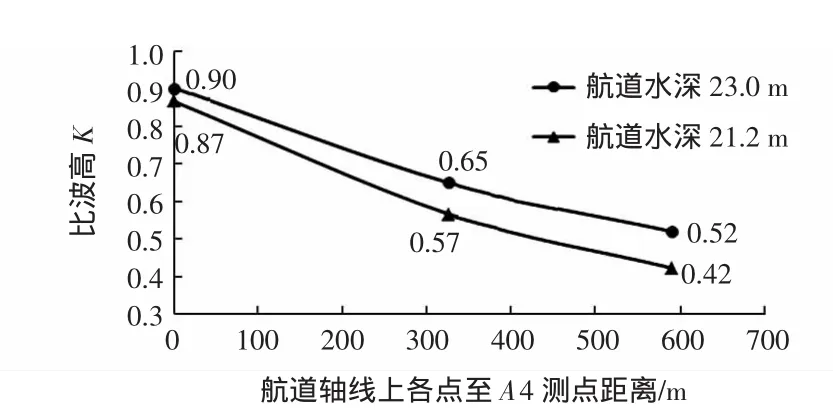
图8 航道轴线比波高
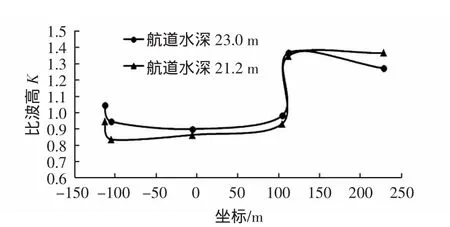
图9 A断面比波高
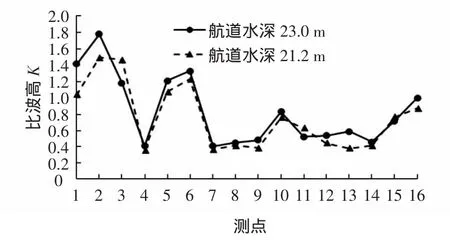
图10 港内比波高
2.3 不同航道等级的波高分布
分析不同航道等级试验中航道附近波浪传播规律。选择极端高水位波浪重现期10 a一遇的条件,图11给出了S向波浪作用下不同航道等级的航道轴线波高沿程变化;图12给出了S向波浪作用下不同航道等级的A断面波高分布;表3给出了不同航道等级航道两侧的最大比波高。
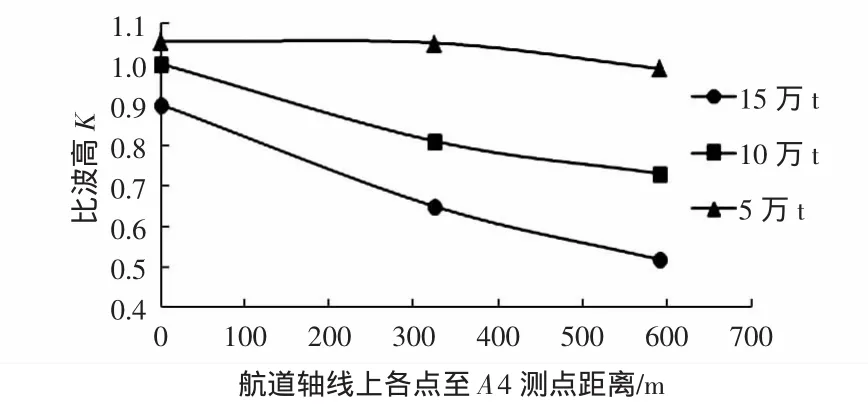
图11 各等级航道航道轴线比波高
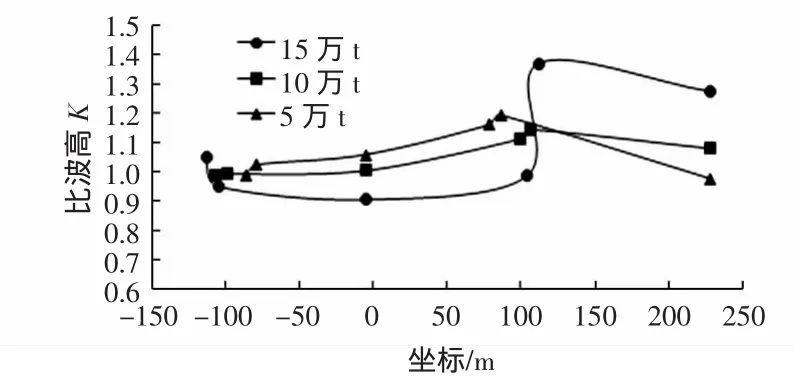
图12 各等级航道A断面比波高
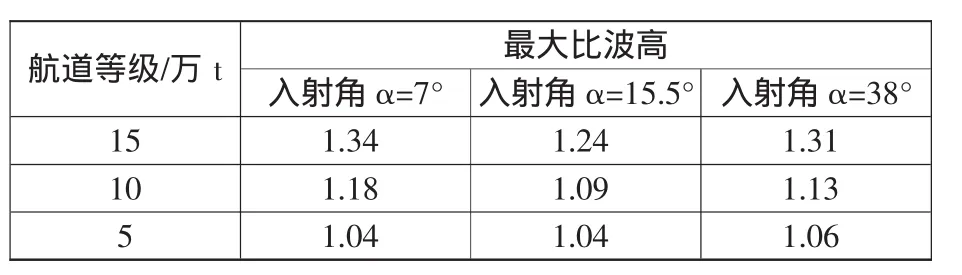
表3 各等级航道两侧最大比波高
随着航道等级的提高,航道水深加深的同时,航道宽度也在增加,在航道轴线上同一测点比波高呈现减小的趋势(见图11),其中的原因,一是航道拓宽使得进入航道的波能略有增加但是波能分布范围更广;二是航道水深加大使得波浪在航道边坡处的折射更为显著,这也是主要的因素。航道A断面波高分布也更加验证了上述两点,5万t和10万t等级航道条件下航道边坡坡顶与航道轴线波高比仅分别为1.13、1.15,而15万t等级条件下则为1.52。这说明了窄浅航道中波能分布更为均衡,折射现象减弱。表3中亦证明了这一点,波浪传播至宽深航道时,边坡上向外折射的波能更多。当波浪入射角改变时,宽深航道中航道两侧最大比波高始终大于窄浅航道。
分析不同等级的航道试验中港内区域的波高分布特征。图13、图14和图15给出了极端高水位波浪重现期10 a一遇条件下,波浪从不同方向入射时各等级航道港内波高分布。当SE和SSE向波浪入射时,波浪入射角较大,航道等级提高使得航道宽度加大,航道水深加深,因此波浪直接进入航道内传递至港内的波能增加,并且入射波浪在迎浪边坡上折射进入港内的波能亦增加,使得港内波高有所增大。当波浪小角度入射时,即S向波浪入射,波浪传播过程中直接入射波能占主导地位,航道宽度增加后,直接入射波能增加,但是水深的增加使得波浪在航道边坡两侧的折射更为显著,加剧了波能向航道外侧的扩散。因此随着航道等级的提高,仅在港区东侧波高有所增大,其余各测点波高减小。
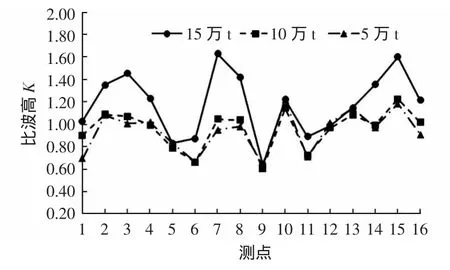
图13 SE向波浪各等级航道港内比波高
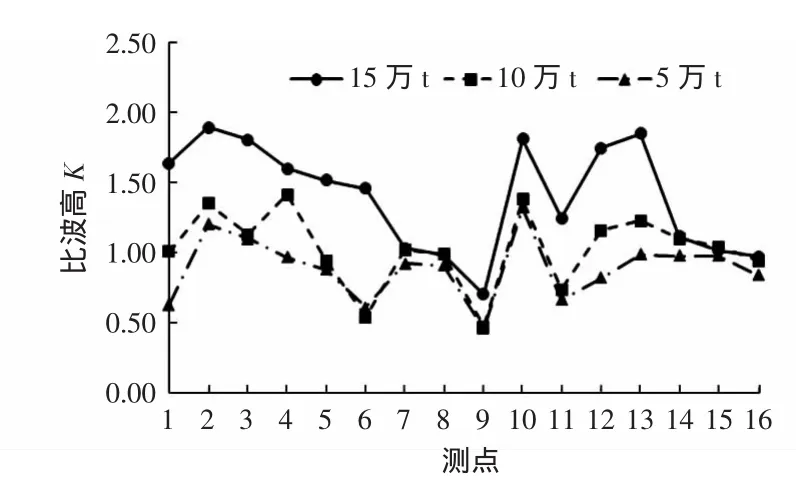
图14 SSE向波浪各等级航道港内比波高
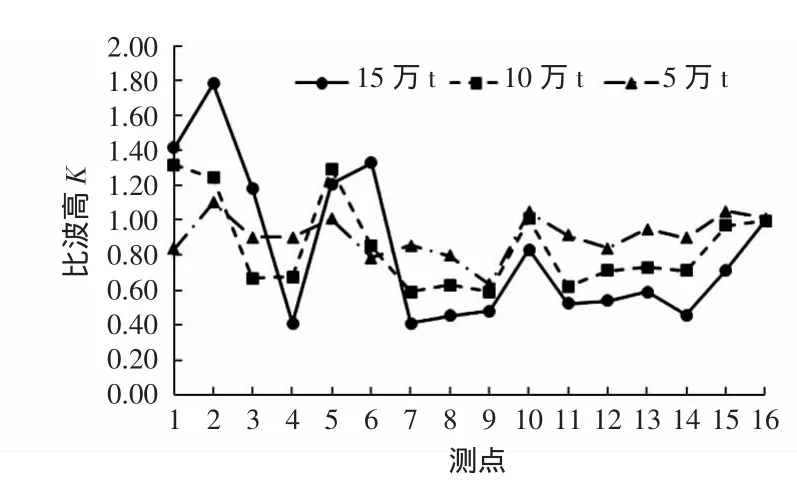
图15 S向波浪各等级航道港内比波高
3 结语
本文通过波浪整体模型实验研究了航道对波浪传播的影响,通过上述的试验结果对比分析可以得到以下结论:
1)开挖航道对于波浪的传播有较为明显的影响,对于不同波浪入射角其影响规律是不同的。波浪小角度入射时,航道中心比波高随着传播距离的增长而逐渐减小,航道内波能向两侧扩散,在两侧边滩形成较大波高带。波浪入射角度较大时,易在航道迎浪侧产生波能集中,背浪侧波高减小。进港航道边坡处的波能集中,影响了进出船舶的航行安全,且不利于口门处防波堤的稳定,在工程实践中应给予重视。试验中也验证了临界入射角的存在,因此应合理选择航道走向,避免常浪向和强浪向波浪以临界入射角入射,恶化港内泊稳条件。
2)航道水深对波浪传播的影响表现在于随着航道内外水深差与航道内水深之比Δd/d内增大,在一定长度范围内航道的折射作用增强。
3)宽深航道对于波浪在航道边坡的折射作用较窄浅航道更为显著。
[1]JA ZWAMBORN,G GREVE.Wave Attenuation and Concentration Associated with Harbor Approach Channels[C]//Int.Conf.of Coast Eng.,1974.
[2]中交天津港湾工程研究院有限公司.烟台港二期工程港外水域波浪传递整体模型试验研究报告[R].1990.
[3]中交天津港湾工程研究院有限公司.大连港大窑湾一期防波堤改造工程整体物理模型试验报告[R].1991.
[4] 赵智帮.关于航道对波浪的作用[J].港工技术,1992(1):l-4.
[5] 李玉成,孙昭晨,滕斌.改善由航道作用使防波堤前波况异常的数值研究[J].海洋学报,1995(14):48-56.
[6] 左其华,杨正己.航槽对不同人射角波浪传播的影响[J].水运工程,1996(1):l-5.
[7]吴达开.小迎浪角时长直航道对波浪传播与变形影响的数值研究[J].水运工程,1997(1):3-13.
[8] 张永刚,李玉成.应用Boussinesq方程对由航道开挖所造成水深变化对波浪传播所产生的异常波况的数值研究[J].海洋工程,1997(15):7-17.
[9] Y SLi,SX Liu,O W H WAI,et al.Wave Concentration by a Navigation Channel[J].Applied Ocean Research,2000.
[10]孙克俐,白志刚,周锡乃.航道外聚集波降波措施研究[J].天津大学学报,2002(3):367-371.
[11]李思源,白志刚,王广聚.减少航道外波浪集聚对策研究[J].海洋技术,2002(21):56-61.
[12]柳淑学,俞聿修.开挖航道对波浪传播的影响[C]//港口工程分会技术交流文集,2005.
[13]董利民,刘爱珍.人工航道对波浪传播规律的影响[J].水道港口,2006,27(2):74-77.
[14]杨宪章,许振沂,臧东生.航道对港内泊稳条件的影响[J].港口工程,1993(3):45-50.
