《数学物理方法》中“行波法”教学方法改革探索

刘 萍，谭朝阳

（电子科技大学 中山学院，广东 中山 528402）

数学物理方法是物理专业的专业课，也是电信、通信、电子科学技术等专业学生的专业基础课之一，众多高校在课程教学中给予了极大重视。电子科技大学中山学院也对这一课程的教学寄予了很大的支持和关注，将其列为必修专业基础课程。数学物理方法既是数学课，也是物理课，学习此门课程既能很好地促进学生进一步掌握物理学的基本原理和数学的基本知识，又能极大地促进学生提高物理抽象思维能力和逻辑推理能力。

数学物理方法这门课的内容非常丰富，各个教材的内容选取并不尽相同。尽管各个教材的内容的选取各异，但大部分教材包含了行波法的内容。关于数学物理方法的教学改革，已经有很多老师们提出了自己的观点和设想［1］。专门关于行波法教学的讨论并不多。行波法在科学研究中，也是一个热点话题［2－3］。在行波法教学中，我们将科研中常用的函数展开法等行波法处理手段以及Maple软件等运用到行波法的教学中，促进教学质量的提高。在本文中我们将与大家分享我们在行波法教学中的一些改革探索。

1 将行波法的教学与非线性数学物理方程的教学结合起来

很多《数学物理方法》的教材都同时介绍了行波法和非线性偏微分方程。我们在讲授数学物理方法的过程中，将这两者结合起来介绍。行波法不仅是求解线性偏微分方程的一种有效途径，而且也是求解非线性偏微分方程，特别是求解非线性波方程的一种重要途径。许多简单的但是重要的非线性波方程的解析解，例如椭圆余弦周期波解、孤立波解、三角函数周期波解等，都可通过行波法获得。例如Burgers方程

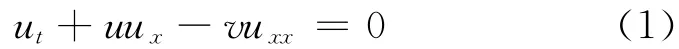
是非常著名的非线性偏微分方程，我们可以用行波法来求解此方程。令，

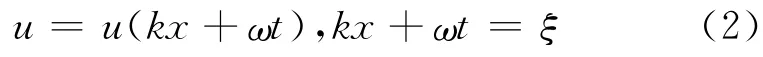
将（2）代入（1）并进行积分处理，就可以得到Burgers方程的行波解。同样地，其他一些非线性偏微分方程也可以用行波法来进行求解。在课堂中，我们给学生介绍了一些非线性波动方程，例如非线性薛 定 谔 方 程［2］、Korteweg－de Vries方 程［3］、Kadomtsev－Petviashvili方程［4］等。将这些非线性方程的求解，作为行波法的教学例子来让学生做练习使用，可以让学生体会到行波法的妙处，促进学生更好地掌握行波法的计算方法，还可以增强学生对非线性科学的了解。

2 将数学计算软件Maple引入行波法的教学中

Maple软件是目前世界上最为通用的数学和工程计算软件之一，在数学和科学领域享有盛誉，有“数学家的软件”之称。Maple系统内置高级技术解决建模和仿真中的数学问题，包括世界上最强大的符号计算、无限精度数值计算，数学和分析功能覆盖几乎所有的数学分支，如微积分、微分方程、特殊函数、线性代数等。在数学物理方法的课堂教学中，我们在教会学生用手计算的同时，也会教学生如何用Maple软件来计算，让学生的“手算”和“脑算”两手都要硬。

下边我们仍以Burgers方程为具体例子来阐述Maple在行波法教学中的渗透使用。例如：如果我们在Maple软件平台中，输入命令“pdsolve（diff（u，t）＋u＊diff（u，x）－nu＊diff（u，x，x））；”，系统就会显示Burgers偏微分方程的求解结果。课堂上让学生比较“手算”和“脑算”的结果，体会电脑计算的便捷。在课堂中，我们还会介绍一些特殊函数待定系数法，即假定方程有椭圆周期波函数、孤立波函数、三角周期波函数等各种各样的函数解，用Maple计算出待定系数，就得到了波动方程各种各样的激发模式。通过这些课堂讲解和演示，让学生掌握行波法的妙处。课堂后，我们还会布置作业，要求学生自己编写小程序来计算一些波动方程的行波解，促进学生更好地掌握行波法的软件计算方法。

3 将波动图形引入行波法教学中

虽然很多数学物理方法的教材将行波法的教学列入了书本，但是直观的二维、特别三维图形在教材里边却并不多见。我们在课堂中向学生展示了大量的波动图形，促进学生对波动现象的直观理解。

例如，我们在课堂上引入了学生非常熟悉的大学物理波动学里边反复介绍的平面波波动表达式［5］

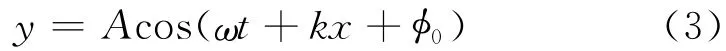
在课堂中，我们给学生展示了三组图形。第一组图形，将（3）式中时间固定，向学生展示波动位移随空间轴的变化，并将时间选取不同值（x，y）的演化图进行比较。第二组图形，将x固定，展示波动位移随时间的演化，并告知学生，此时波动退化成质点的振动。第三组图形，我们从不同角度展示了（x，t，y）三维时空演化图。同时，还可以借助数学软件，展示波动图形的动态变化，加深学生对“行波”的印象。

“数学物理方法”是高校教学中公认的课程难度较大，学生学习兴趣比较低的课程。在课堂教学中，如果简单的讲解书本知识，照本宣科，很难引起学生的学习兴趣。我们通过引入数学软件，介绍具有强烈物理背景的非线性波动方程，同时展示大量的图形来增强行波法的教学效果。同时，课堂上展示的所有计算方法、计算程序、图形，都比较简单，同学在课堂外也很容易重复，加深他们的成就感。学生在行波法教学中学到的知识将更好的促进他们对《大学物理》、《电磁场与电磁波》等涉及波动、振动的课程的理解。

［1］蒋然.数学物理方法教学改革中的若干想法［J］.中国科技信息，2010（9）：33－34.

［2］刘萍，李子良，楼森岳.一类耦合非线性Schodinger方程的Painleve性质、严格解及其在大气重力波中的应用［J］.应用数学和力学，2010，31（11）：1308－1329.

［3］Ping Liu，Pei－Kai Fu.Modified（2＋1）－dimensional displacement shallow water wave system and its approximate similarity solutions［J］.Chin.Phys.B，2011（9）：5－6.

［4］Ping Liu and Sen－Yue Lou.A（2＋1）－Dimensional Displacement Shallow Water Wave System［J］.CHIN.PHYS.LETT.，2008（9）：10－12.

［5］胡盘新，汤敏骏，钟季康.普通物理学简明教程上册［M］.2版.北京：高等教育出版社，2004.