变分法在量子力学中的应用
2013-01-19邓小辉许成科汪新文
邓小辉,许成科,汪新文
(衡阳师范学院 物理与电子信息科学系,湖南 衡阳 421008)
0 引 言
1926年,奥地利物理学家薛定谔提出用一个波方程来描述微观粒子体系的运动行为,即薛定谔方程[1]。求解此方程,就可得到体系的波函数,那么体系的一切性质都能被确定[2]。随后的考虑了相对论效应的狄拉克方程的确立[3],让人们似乎看到“现在量子力学的普遍理论业已完成,作为大部分物理学与全部化学的物理定律业已完全知晓,而困难仅在于把这些定律确切应用将导致方程式太繁杂而难以求解。”。正如狄拉克所说,随着体系的增大,薛定谔(或者狄拉克)方程几乎是不可解的。因此,各种近似方法应运而生。在量子力学中,求解薛定谔方程有两种应用范围极广的近似方法:微绕法和变分法。对于束缚定态,它是基于能量本征值方程(即不含时间的薛定谔方程)与能量变分原理的等价性,通过求能量的极值得到能量本征值方程的解。在处理具体问题时,总是采用波函数某种特殊的变化去代替最普遍的任意变分,这样就可得到依赖于波函数特殊形式的近似解[4]。这种方法称为变分法。
变分法的优点在于运用它求解不受什么限制,只要选取好的变分函数,就能很好地得到体系的基态性质。因此利用变分法来求解量子体系具有方便、简单和物理意义明确的优势。本文将主要研究变分法在量子力学中的应用。为与求解量子体系的基态性质相关的科研和教学活动提供一个参考。
1 变分法概要
可以证明某个微观体系的薛定谔方程

就是下列变分问题的欧拉微分方程[5]。这个变分问题就是能量积分
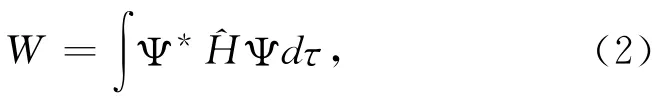
为极小,即
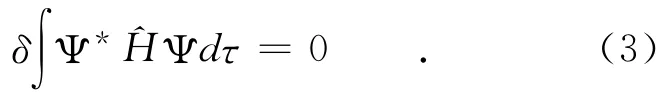
H为体系的哈密顿量,可写为

其中波函数满足归一化条件
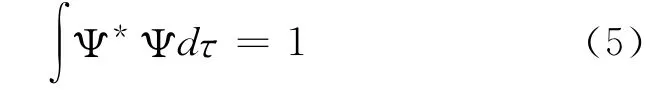
把(4)式代入(3)式,施行部分积分得到

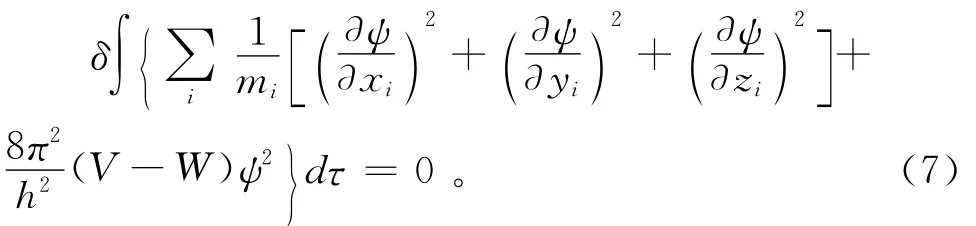
由欧拉微分方程,经整理后即可得到薛定谔方程(1)式。至此我们就证明了微观体系的薛定谔方程就是使其能量积分取得极值时的欧拉微分方程。可见在量子力学中,不必从薛定谔方程出发来研究,而从(3)式或者(7)式出发来研究即可。这样问题就变成求一函数ψ,它将使(3)或者(7)中的积分变为极小。这就是量子力学中的变分原理[5]。
2 一个例子:一维谐振子
无论在经典物理还是在量子物理中,一维谐振子都和很多物理现象相关。简单来说,任何体系在稳定平衡点附近的运动都可以近似看成一维谐振子。如双原子分子的振动,晶体结构中原子和离子的振动,核振动等等[6]。下面我们用上面的变分原理来讨论一维谐振子。假设谐振子的质量为m,沿x轴作直线运动,那么受到的势能为
体系的哈密顿量为
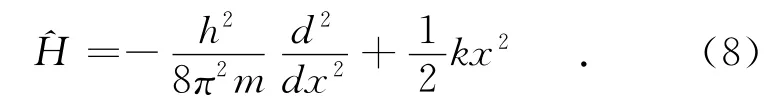
选择试探波函数ψ=Ce-λx2,由归一化条件(5)得到。那么,
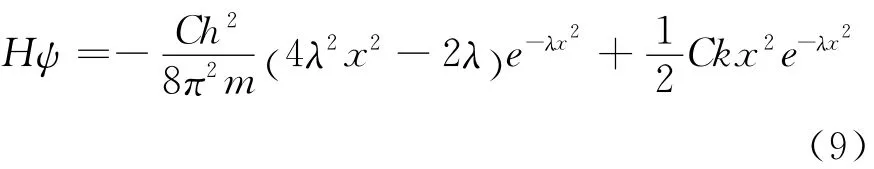
体系的能量积分为
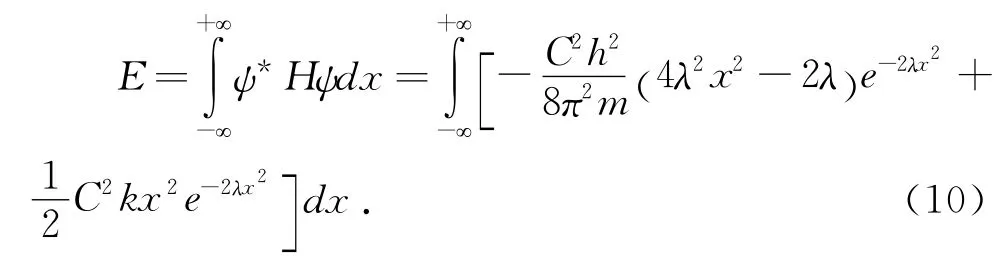
对上式展开积分,应用积分公式
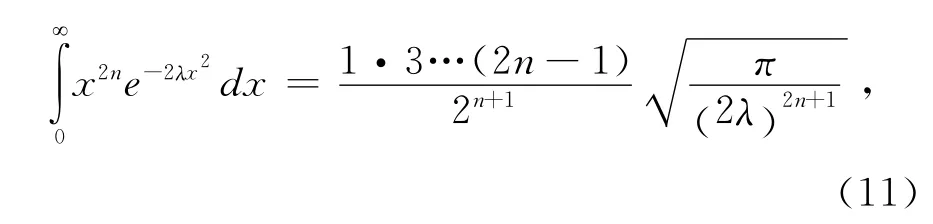
可算出

E为一极小的条件为
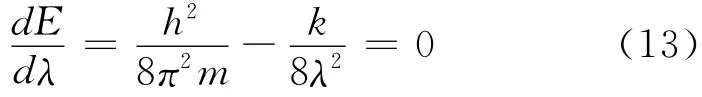
可解得

代入(12)式,得到体系最低能量值为

相应的波函数为
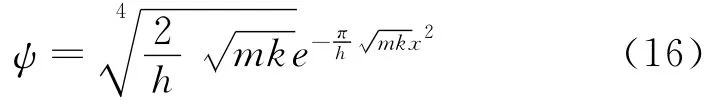
令
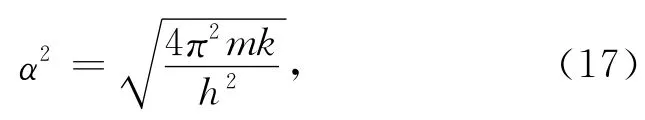
(16)式化为一种更简单的形式
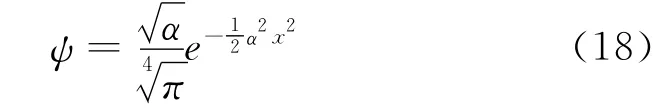
这种结果与严格求解得到的结果完全相同[7],说明我们选取的变分函数很好。
几种α下波函数图如图1。波函数满足高斯型分布,在x=0出有个明显的峰。随着α的降低,峰值逐渐降低,峰的宽度越来越大。波函数几率密度分布和波函数的分布曲线形状一样,也是随着α的降低,波函数几率密度分布趋于更为发散。值得指出的是,用变分法解出的波函数几率分布和经典理论下得到的几率分布明显不一样。变分法得到的波函数在x=0处的几率最大,如图1。
必须指出,变分虽然能简单、方便地求解体系的基态性质,但它是一种近似方法,它的近似性来源于用参数的变化代替了普遍形式的任意变分。显然,只要选取的波函数满足归一化条件和边界条件,波函数中参数愈多,尝试波函数的变化愈普遍,所得结果就愈好。如果尝试波函数与精确解的差为Δ量级,则能量本征值与精确解的差为Δ2量级,因而即使用较为粗糙的尝试波函数也可得到近似性很好的能量本征值。考虑到不同能量的本征函数彼此正交,也可以由低至高逐级求激发态能量的近似值,其近似性较基态为差。变分法的优点在于运用它求解不受什么限制,但是由于结果的好坏完全取决于尝试波函数的选择。因此选取物理意义明确的尝试波函数至关重要。

图1 几个典型的α下的线性谐振子波函数和位置几率密度分布图
3 结 语
本文主要研究了变分法在量子力学中的应用。证明了微观粒子的薛定谔方程就是其能量积分取极小值时的欧拉方程。求解薛定谔方程可以转换为去确定体系的能量积分的最小值。为量子力学中求解基态问题提供了一种参考方法。最后以一维谐振子为例,用变分法求得了其基态能量和波函数,其结果和严格求解得到的基态能量和波函数符合得很好,说明变分法在量子力学中是一种有效的求解基态性质的方法。
[1]E.Schrodinger.Quantisierung als eigenwertproblem[J].Ann.d.Phys.,1926,79:361.
[2]B.Hoffmann.The Strange story of the quantum[M].Dover publications,Inc.1959:60-80.
[3]P.A.M.狄拉克.量子力学原理[M].陈咸亨,译.北京:科学出版社,1979:258-282.
[4]老大中.论完全泛函的变分问题[J].北京理工大学学报,2006,26(8):749-752.
[5]芶清泉,黄树勋.原子结构的变分计算[M].成都:成都科技大学出版社,1989:1-19.
[6]习岗.大学基础物理学[M].北京:高等教育出版社,2008:60-428.
[7]周世勋.量子力学教程[M].北京:高等教育出版社,2001:38-44.
