GNSS接收机自主完好性监测算法研究

陈 婷，佀 荣，史彦芳

（西北工业大学 电子信息学院，陕西 西安 710129）

现有的四大全球导航卫星系统分别是：我国正在建设的北斗第二代导航系统、美国GPS、俄罗斯GLONASS和欧盟的GALILEO系统。随着全球卫星导航卫星系统的建设，可见卫星数目逐渐增多，同一历元时刻可见星从单GPS的8、9颗上升到近40颗。多卫星导航系统组合导航在精度、完好性、可用性等方面性能明显要优于单系统，将成为今后发展的必然趋势，其中多星座下的信号完好性监测性能也被越来越多的国内外学者研究。

完好性增强的方法[1]主要有卫星自主完好性监测（Satellite Autonomous Integrity Monitoring，SAIM）、增强系统（广域增强系统（Wide Area Augmentation System，WAAS）与局域增强系统（Local Area Augmentation System，LAAS））及接收机自主完好性监测3种。接收机自主完好性监测是利用接收机自身的冗余观测值进行卫星故障的监测识别，它无需外部设备的辅助，花费较低，容易实现，是目前应用较为广泛的一种完好性监测算法。

1 完好性的概念

关于完好性，美国航空无线电技术委员会（Radio Technical Commission for Aeronautics，RTCA）给出的定义[2]是：当系统发生故障，系统信号不能用于导航定位时，系统向用户提供及时报警的能力。这一概念包括以下几个指标：

1）报警限值：当用户定位误差超过系统规定的某一限值时，系统向用户发出警报。

2）示警耗时：用户定位误差超过报警限值的时刻和系统向用户显示这一警报时刻的时间差。

3）示警能力：在系统覆盖区域内，系统不能向用户发出警报的面积百分比。

4）失误概率：示警能力以内的用户定位误差超过报警限值和规定的示警耗时，而系统又没有向用户发出警报的概率。

2 RAIM判定流程

RAIM技术的基本原则是增加观测卫星的数量，利用冗余度信息进行判定。RAIM算法对故障卫星的监测识别受可见卫星数目和卫星几何分布的影响，在某些地区，可能由于卫星几何布局等因素的影响，无法同时满足所有完好性性能指标，此时的完好性监测结果将不可信。具体判定流程[3]如图1所示。

图中n表示可见卫星数，HPL表示水平保护限，HAL表示水平告警限，不同的导航阶段对HAL有不同的要求，T为统计监测量。由于在进行RAIM实现的过程中，采用的是余度技术，即增加观测卫星数，因此，在进行卫星导航信号接收的同时需要首先判断当时可见卫星的数目，倘若少于5颗可见定位卫星则提醒用户此时RAIM无效，需要重新接收定位信号；其次，需要根据性能指标对当前可见星的几何分布进行判断，决定其是否适合进行完好性监测。根据接收到的卫星数据得出水平保护限HPL，然后与系统给定的水平告警限HAL相比较，如果HPL小于HAL，说明此时可见星几何结构满足RAIM要求，此时的完好性监测结果是有效的；反之无效，此时需要重新接受卫星信号进行判断，这种情况通常称为完好性要求下的可用性判断。在进行故障卫星监测识别之前，必须对完好性要求下的可用性作相应的判断。

图1 RAIM判定流程Fig.1 Flow chart of RAIM algorithm

3 卫星故障的RAIM算法

RAIM是通过用接收机端的冗余观测信息监测GNSS完好性的一种方法。RAIM应该提供如下的信息：RAIM技术是否可用，卫星系统是否存在异常，能否确定故障卫星，导航解能否满足实际应用的要求。

普遍采用的RAIM算法是基于当前历元观测量的 “快照”（Snapshot）方法。基于Snapshot模式的算法主要包括Lee YC于1986年提出的距离比较法[4]、Parkinson于1988年提出的最小二乘残差法和Sturza于1988年提出的奇偶矢量法。这3种方法对于一个故障的情况有较好的效果且被证明是等效的。20世纪90年代，Brown改进了奇偶向量法。奇偶矢量法计算相对简单，已普遍采用并被RTCA SC-159推荐为基本算法。下面介绍奇偶矢量法的基本原理。

可见卫星数为n，GNSS观测方程线性化后可写为：

其中：y代表实际测量伪距与预测伪距的差值，预测伪距是根据标称的位置和时钟偏差得到的，y是一个n×1测量矢量；x代表实际位置与标称位置偏差的3个分量和用户时钟偏差，它是4×1用户状态矢量；H表示一个n×4线性联接矩阵，前3列由相应角的余弦值组成，第4列是一个时间列；表示由于选择可用性、接收机噪声及传播不确定性带来的测量误差矢量，它是一个n×1误差矢量。假设服从标准正态分布，则最小二乘解为

定义奇偶矩阵P，它满足PH=0且PPT=In-4。对H矩阵进行QR分解可得P，则有Py=Pε，定义奇偶向量p=Py=Pε。pTp定义为检测统计量，它反映了观测量误差的大小，且服从自由度为n-4的x2分布。由误警概率可求得检测门限，当检测统计量大于检测门限时，则认为观测卫星中存在故障卫星。

当检测出系统故障时，还需要进一步确定故障卫星并将其隔离，以保证故障卫星不会对定位结果产生不良影响。标准的故障隔离方法[5]见参考文献[5]。将奇偶矩阵P用其列向量表示为 P=[p1，…，pi，…，pn]，其所有列向量张成的奇偶空间的维度为n-4。每一个列向量pi对应于一颗卫星，称为该颗卫星的特征矢量，将获得的奇偶矢量在每一个特征矢量的方向上进行投影，具有最长投影长度的那颗卫星就是故障星。

4 多星座RAIM算法

多星座RAIM利用各系统空间的卫星能够提供比独立系统更好的卫星定位几何结构[6]，使得RAIM的性能得到大幅度提高。对于多星座RAIM算法需要考虑更多方面的问题，Ober PB和Harriman D指出在考虑不同类型卫星存在而且它们具有不同的故障特性时RAIM算法需要进行适当的调整[7]。Steve Hewitson在对GNSS多星座系统的RAIM性能进行了仿真分析研究，其结果如表1所示。

表1 独立星座与多星座RAIM可靠性性能Tab.1 Dependability of single-constellation and multi-constellation

表1给出的结果是在RAIM可用性满足的情况下=80%，=0.5%条件下的测试结果，γ，α分别为可靠性概率值，显著性水平值。

5 仿真及分析

RAIM性能主要从故障检测率、故障识别率两个指标进行衡量。

在仿真中[8]，用户星置于海拔0 m高度的固定位置，采样间隔为30 s，监测12 h，选取某颗卫星为故障星，在此观测卫星的伪距中加入故障偏差，偏差值从0 m递增到200 m，步长为10 m，所有在用户位置上观测到的可见卫星都用于监测，仿真结果如图2和图3所示。

通过图2对比单GPS与“GPS/GALILEO/BEIDOU”组合导航的故障检测率可以发现，组合导航的故障检测能力要优于单系统导航故障检测能力。这体现在当伪距偏差达到140 m时，组合导航系统能100%检测到故障；GPS单系统由于存在不可用时刻，故障检测率只能达到96%。组合系统通过增加可见卫星数目，增加RAIM的冗余信息，提高RAIM的可用性，减少RAIM空洞，在一定程度上能够提高RAIM算法性能。

图2 系统故障检测率Fig.2 Failure-detecting ratio of receiver

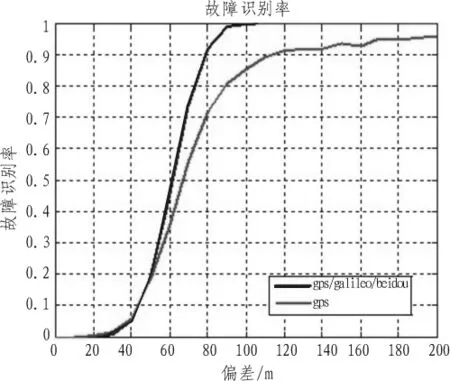
图3 系统故障识别率Fig.3 Failure-excluding ratio of receiver

通过对比图3单系统导航与组合导航的故障识别率同样可以发现，组合导航的故障识别能力要优于单系统导航故障识别能力。其原因与组合导航的故障检测能力要优于单系统导航故障检测能力的原因相同。

6 结 论

文中分析了接收机自主完好性监测的判定流程，且分别从单星座系统和多星座组合系统两种条件下深入分析了RAIM算法。仿真结果表明，多星座组合系统下RAIM算法可以提高传统的单星座系统下RAIM算法的故障检测率和故障隔离率。

[1]卢德兼，陈秀万.GNSS系统接收机自主完好性监测算法[J].计算机工程，2009，35（11）:10-12.LU De-jian，CHEN Xiu-wan.Algorithm for global navigation satellite system receiver autonomous integrity monitoring[J].Computer Engineering，2009，35（11）:10-12.

[2]卢德兼.多星座全球导航卫星系统完整性分析[J].计算机工程，2010，36（11）:238-240.LU De-jian.Analysis of integrity for Multi-constellation global navigation satellite system[J].Computer Engineering，2010，36（11）:238-240.

[3]李飞，段哲民，龚诚.GPS接收机自主完好性监视算法研究及仿真[J].测绘科学，2009，34（1）:136-137.LIFei，DUANZhe-min，GONGCheng.Research and simulation on RAIM algorithm of GPS[J].Science of Surveying and Mapping，2009，34（1）:136-137.

[4]郭婧，陆明泉，冯振明，等.三频GNSS接收机的RAIM算法研究[J].宇航学报，2011，32（8）:1734-1739.GUO Jing，LU Ming-quan，FENG Zhen-ming，et al.Research on RAIM algorithm for triple-frequency GNSS receiver[J].Journal of Astronautics，2011，32（8）:1734-1739.

[5]Sturza M.Navigation system integrity monitoring using redundant measurements[J]．Navigation:Journal of the Institute of Navigation，1989，35（4）:483－501．

[6]王尔申，张淑芳，胡青.GNSS接收机自主完好性监测算法研究[J].通信技术，2010，43（217）:213-216.WANG Er-shen，ZHANG Shu-fang，HU Qing.Research on autonomousintegrity monitoringalgorithmsof GNSSreceiver[J].Communications Technology，2010，43（217）:213-216.

[7]Rulkov N F，Sushchik M M，Tsimring L V，et al.Digital communication using chaotic pulse position modulation[J].IEEE Trans on Circuits System，2001，48（06）:1436-1443.

[8]卢虎，廉杰.北斗用户机自主完好性监测研究[J].空军工程大学学报：自然科学版，2010，11（3）:53-57.LU Hu，LIAN Jie.Research on RAIM algorithm of beidou receiver[J].Journal of Air Force Engineering University：Natural Science Edition，2010，11（3）:53-57.