基于单电磁矢量传感器的MUSIC联合参数估计方法

张凯

（南京航空航天大学 电子信息工程学院，江苏 南京 210016）

单电磁矢量传感器便可以实现入射电磁波信号的DOA和极化参数估计，具有经济、简单、安装方便、节省空间等优点，近年来，利用单个电磁矢量传感器进行DOA和极化参数估计问题成为阵列信号参数估计的研究热点之一，受到学术界的高度重视。

在众多高分辨DOA估计算法中，基于特征分解的MUSIC算法是空间谱估计理论的标志性算法，标志着空间谱估计进入了繁荣阶段。以往的任何算法，如MVM和CPF等都是对阵列接收数据的协方差矩阵进行直接的处理，而MUSIC算法的思想是将接收数据协方差矩阵按特征分类。它将观测空间分解为相互正交的信号子空间和噪声子空间，利用这两个空间的正交性来估计信号的参数（DOA、极化参数等）。

文中研究在有电磁波信息链的条件下，基站发射的测控电磁波的极化椭圆率不随坐标系变化而变化，即在发射端和接收端是一致的，飞行器通过单电磁矢量传感器估计DOA和极化角。

1 旋转矩阵的指数表示

在三维中，旋转可以通过单一的旋转角θ和所围绕的单位方向向量 v=（x，y，z）来定义。 三维空间任意旋转矩阵[1]为：

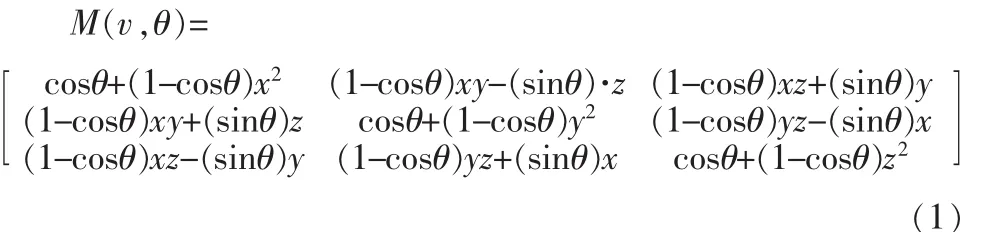
式（1）可由单一矩阵的指数函数形式来表示：

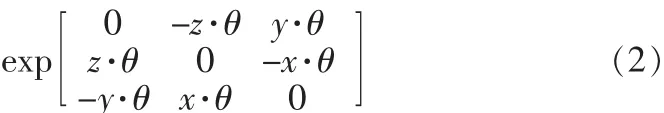
证明：记矩阵

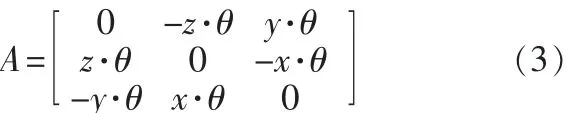
对于任意的n阶矩阵A，存在可逆矩阵P，使得P-1AP=J为Jordan标准型[2]。其中，

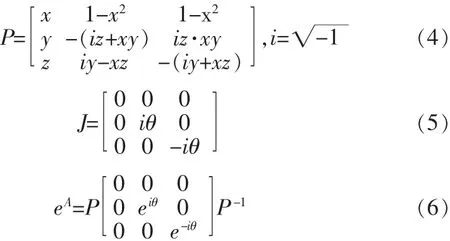
把（4）（5）带入（6）经过化简计算得式（1）结果。 证毕。称式（2）为旋转矩阵的生成元表达方式。其中，

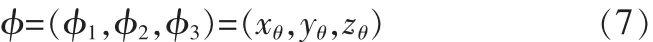
称作旋转向量。下面介绍旋转向量的求解。

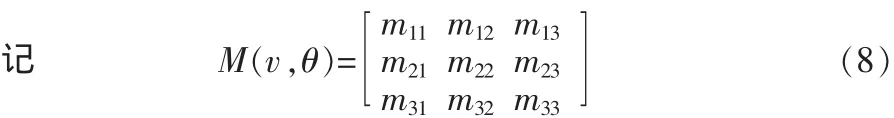
表示 （1） 式中任意一个三维旋转矩阵，mij，i=1，2，3；j=1，2，3表示旋转矩阵的第i行j列的每一个元素。

任意旋转矩阵 M（v，θ）的迹满足

因此由（7）（10）（12）可得到旋转向量 φ。

2 单电磁矢量传感器信号接收模型

电磁波信号s（t）沿-u方向传播，如图1所示。电磁波空间到达方向用方位角和仰角（φ，θ）表示，φ∈=[0，2π]，θ∈[0，π]。时谐平面电磁波波达平面内电场和磁场矢量呈椭圆状旋转，极化状态用极化椭圆描述子（γ，η）表示，γ∈[-π/2]，η∈[-1π/4，π/4]，如图2所示。当η=0时，极化椭圆压缩为长轴所在的直线，η=±π/4时，极化椭圆为圆形。在测控应用中，极化椭圆率η可设定为一个或几个固定值，这样信号空域-极化域的四个参数中有一个明确。本文正是考虑在测控应用中的信号参数估计。

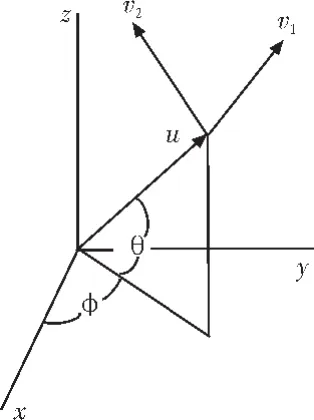
图1 接收信号的正交矢量Fig.1 Orthonormal vector triad

设 XE（t），XH（t）分别为接收信号的 3×1 维电场分量和 3×1 维磁场分量，NE（t）和 NH（t）分别为 3×1 维电场噪声矢量和3×1维磁场噪声矢量。假设噪声均为零均值的复高斯白噪声，电场噪声功率和磁场噪声功率分别为和。对于所有的t和s，以下两式成立：

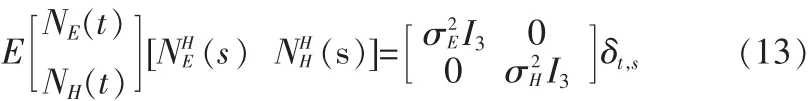
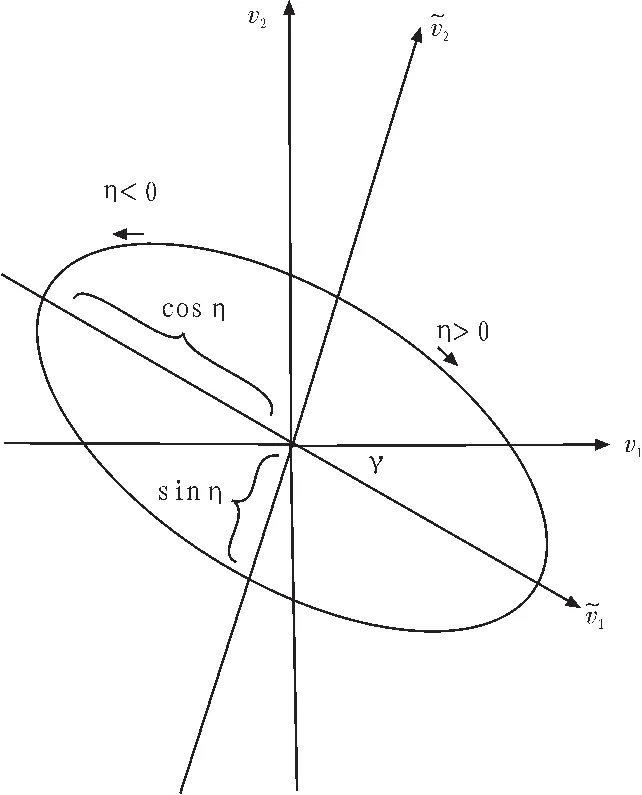
图2 空间极化电磁波椭圆状旋转电场Fig.2 Electric polarization ellipse

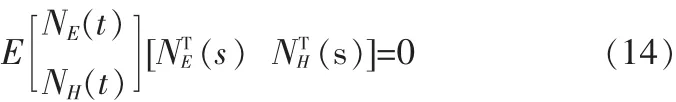
全电磁矢量传感器接收信号描述为[3]：

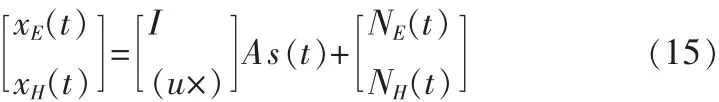
其中I为3×3单位矩阵，u为电磁矢量传感器接收到的指向信号源的单位向量[3]，

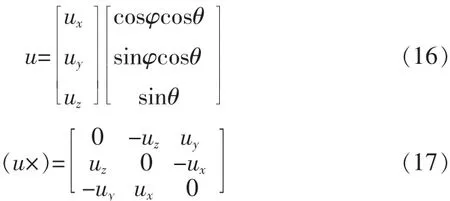
A=VQw为极化-空域导向矢量[4-5]，

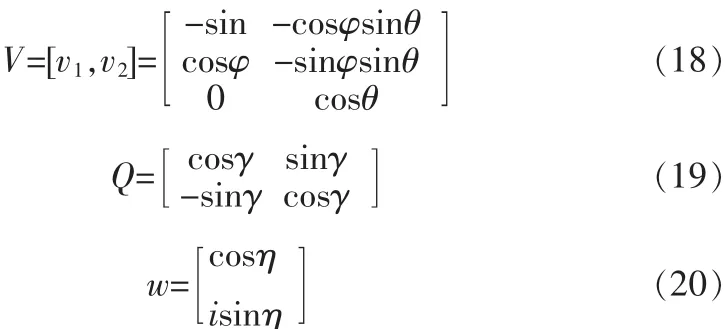
信号的数学描述是研究运动平台姿态的基础，传统的描述表达不利于姿态估计计算的展开，将全电磁矢量传感器接收信号极化-空域导向矢量A=VQw演化为

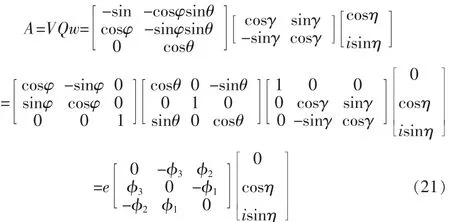
这样的导向矢量利用旋转向量 φ=（φ1，φ2，φ3） 来表达便于姿态参数的计算，显出信号中包含的三维姿态信息，也显示出极化域的自由度只有2。考虑以下关系：

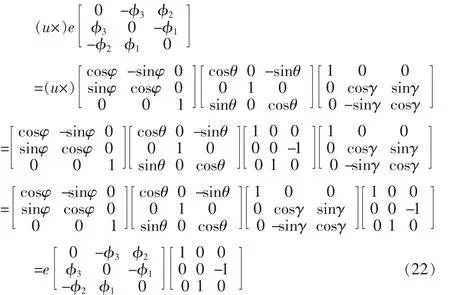
得到（15）中电磁矢量传感器接收模型变为

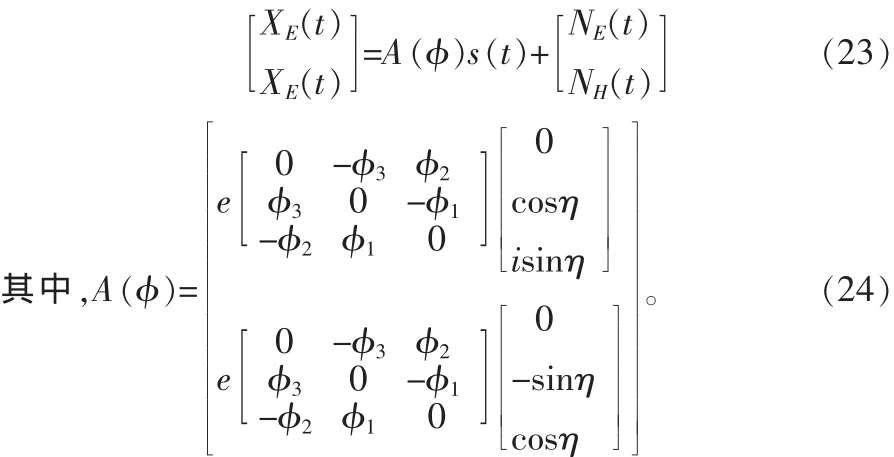
3 波达方向和极化角估计

常规MUSIC算法的基本出发点是对阵列输出数据的协方差矩阵进行特征分解，而单个电磁矢量传感器相当于一个六元阵列，其输出是六维的复矢量，仍能获得这样的“阵列”输出协方差矩阵。所以将常规MUSIC算法应用到单个电磁矢量传感器中是完全可行的。

但是需要注意：这种特殊的六元阵列也和普通的阵列有所不同，在通常的阵列信号处理中，由于每个传感器的“对等性”，常假设每个阵元（标量传感器）具有相同的噪声功率σ2。以六元的普通阵列接收K个信号为例，自相关矩阵的特征值有两部分组成[6]：前K个特征值为σ2+α2i，后6-K个特征值全部等于噪声功率σ2。这样只要有足够的信噪比，就可以将前K个较大的特征值和6-K个较小的特征值区分开来。但是在单电磁矢量传感器中，本文中假设电场噪声功率和磁场功率不完全相等，所以以上条件并不满足，则不能完全将阵列MUSIC算法照搬到单矢量传感器中，需要另作讨论。

假设个独立的完全极化电磁波信号入射到单个电磁矢量传感器上，第个信号的波达方向为，极化倾角为，极化椭圆率=已知。定义新的测量模型：

其中，r为磁场噪声标准差和电场噪声标准差的比值：r=σH/σE，并设 σ2=。则（20）式中的噪声模型满足对于所有的 t和s，

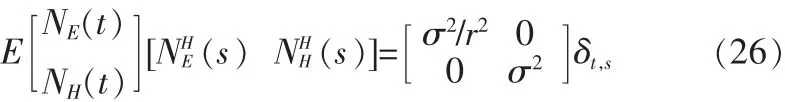
这样（25）式可以写为：

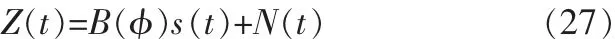
B（φ）为导向矢量矩阵A（φ）的前三行元素同时乘以 r后三行元素不变所形成的等效导向矢量矩阵噪声模型可以表示为：

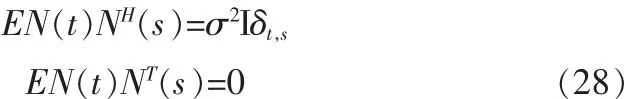
这样（27）（28）所示的信号模型满足MUSIC算法的条件。

输入数据协方差矩阵为：

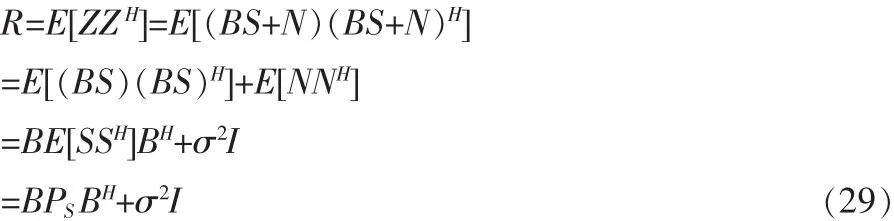
其中RS是信号协方差矩阵，对R进行特征值分解得到

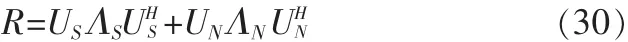
其中，US是由K个大的特征值对应的特征向量张成的子空间，称为信号子空间，而UN是由6-K个小特征值对应的特征向量张成的子空间，称为噪声子空间。由（10）（11）可得：

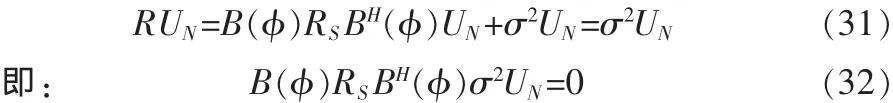
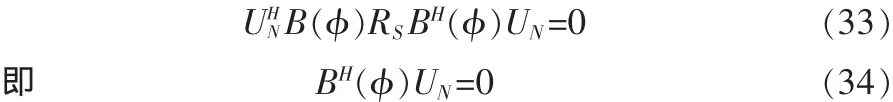
这说明B（Θ）的各列向量与噪声子空间正交，故有：

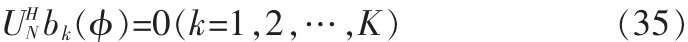
由以上噪声特征向量和导向矢量的正交关系，得到MUSIC算法的空间谱函数为：

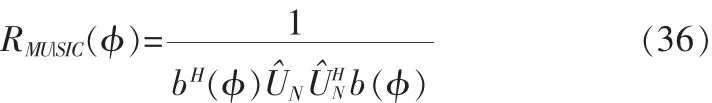
使 φ1，φ2，φ3变化，通过搜索寻求式（36）谱峰对应的 φ1，φ2，φ3。

4 仿真实验

本实验考查两个独立的完全极化测控电磁波入射到单个电磁矢量传感器上，两个信号的参量分别设置为（φ1，θ1，γ1，η1） =（270°，60°，30°，15°）， （φ2，θ2，γ2，η2） =（60°，30°， -60°，15°）。信噪比SNR=10 dB，附加噪声为高斯白噪声，噪声方差为σ2=1，r=2采样点数N=1 000。实验分别考查相同入射信号，通过矩阵乘积的形式和矩阵生成元形式在估计信号参数上的性能。

图3是在固定极化椭圆角情况下，得到的谱图（峰值均放大100倍后图），观察4个谱图上面两个，我们知道在极化角正好为入射信号的极化角时，出现两个光滑尖锐谱峰，其中最大峰对应的方位角和俯仰角也与入射信号一致；观察四个谱图的下面两个当极化角不为入射信号的极化角时，出现两个或多个最大谱峰，谱峰不光滑也不尖锐。

采用矩阵生成元方式是，由前面两个入射信号得到的旋转向量分别为 （φ11，φ12，φ13）=（-1.209 2，-0.442 6，-1.621 8），（φ21，φ22，φ23）=（1.200 1，0.107 2，1.200 1）， 通过使（φ1，φ2，φ3）变化搜索得到的两个谱峰为（，）=（-1.207 0，-0.441 3，-1.643 0），（，，）=（-1.193 1，-0.108 0，-1.199 5），基

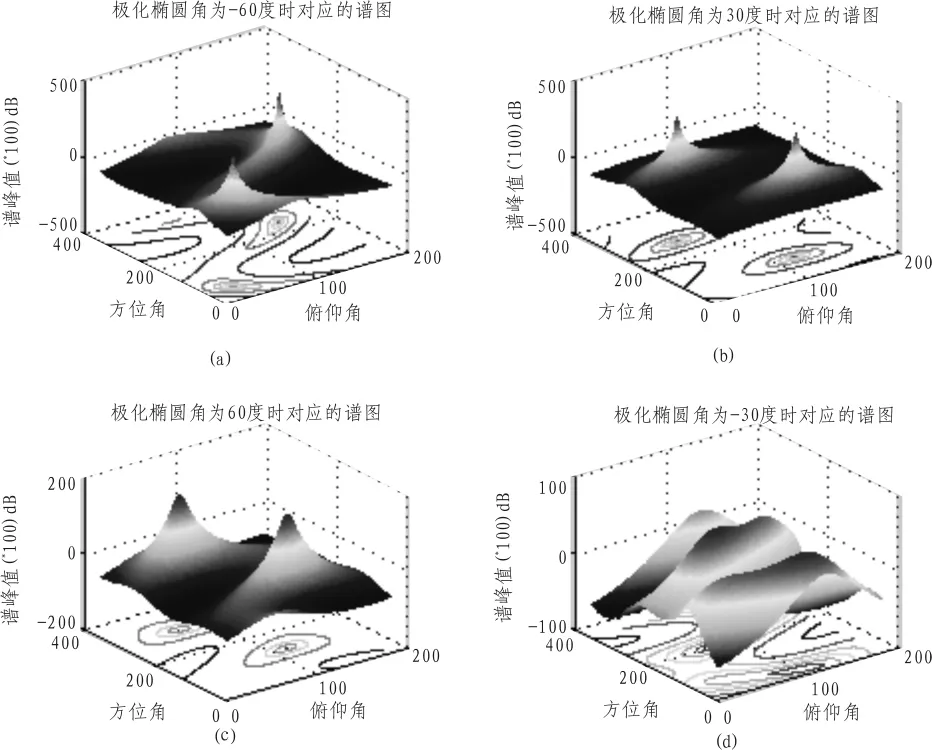
图3 矩阵乘积形式的谱图Fig.3 Spectrum of matrix multiplication form

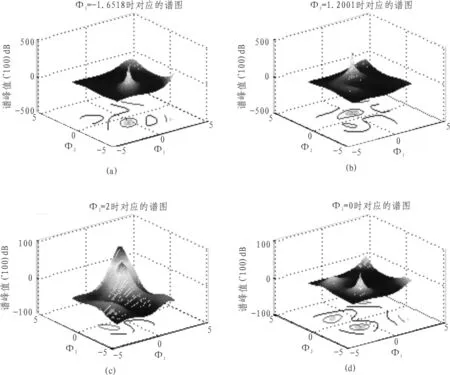
图4 矩阵生成元形式的谱图Fig.4 Spectrum of matrix generation element form

5 结 论

文中主要介绍了单电磁矢量传感器对测控电磁波进行信号DOA和极化角估计的问题。将传统的MUSIC算法拓展到电磁矢量传感器中，对极化-空域导向矢量用一种矩阵指数的形式来表示，简化了参数估计，仿真实验也验证了此方法的有效性。本文是在对电磁波信号、噪声、传播介质、工作环境等都做出了合理的理想化假设基础上的提出的参数估计算法，没有考虑天线的交叉极化、散射干扰、多径效应、基站误差等因素，实际应用估计精度有所降低。

[1]Shuster M D.A survey of attitude representations[J].Journal of the Astronauti cal Scienece，1993，41（4）：439-517.

[2]戴华.矩阵论[M].北京:科学学出版社，2007.

[3]Nehorai A，Paldi E.Vector-sensor array processing for electromagnetic source localization[J].IEEE Trans.on SP，1994，42（2）:376-398.

[4]徐振海.极化敏感阵列信号处理的研究[D].长沙:国防科技大学，2004.

[5]王兰美.极化阵列的参数估计和滤波方法研究[D].西安:西安电子科技大学，2005.

[6]张贤达.现代信号处理[M].北京:清华大学出版社，2002.