一套新的3He 普适唯象光学势参数
2013-01-17徐永丽苏新武
徐永丽,苏新武,林 海
(山西大同大学物理与电子科学学院,山西大同037009)
光学模型[1-2]是核反应理论中最基本的理论模型之一,在核反应理论中有很广泛的应用。它能描述弹性散射角分布、去弹截面和总截面,计算复合核反应、预平衡反应的穿透系数、扭曲波玻恩近似方法中的扭曲波和各种反应逆截面等。光学势是光学模型的关键。对光学势的研究主要通过两种方法,即唯象光学势和微观光学势。从核力的性质、核结构的知识和微观光学势的研究的定性结论,可以写出光学势与径向距离r,靶核的质量A,电荷数Z,以及入射粒子的能量E 的函数关系式。 其中包含一些待定的具有物理上合理的参数,再通过调节这些参数使得由光学模型计算的截面和角分布等均能较好地符合实验数据,用这种方式确定的光学势称为唯象光学势。光学模型在计算核子的弹性散射和吸收方面的成功,可以使其应用到计算复杂粒子的散射和吸收。复杂粒子的普适唯象光学势是在一定能区和核区范围内,通过调节光学势的参数,使得用光学模型计算的结果能符合大量反应截面以及弹性散射角分布实验数据,可以对一些没有实验数据的能区和核区提供一定的预言作用。
到目前为止,共有4 套3He 普适唯象光学势。1971 年,Becchetti 和Greenlees(BG)给出了靶核质量数为A>40,3He 能量为E<40 MeV 的普适唯象光学势[3];1987 年,Trost 等人给出了靶核质量数为10≤A≤208,3He 能量为10≤E≤220 MeV 的普适唯象光学势[4];2009 年,庞等人[5]给出了靶核质量数为40≤A≤209,3He 能量为30≤E≤217 MeV 的普适唯象光学势(GDP08)。同年,梁等人也给了一套3He普适唯象光学势[6]。在这几套参数中,除了梁等人给的普适唯象光学势,其它普适唯象光学势的获得都没包括反应截面的实验数据。
本论文就是通过同时符合靶核质量数为20≤A≤209,3He 入射能量从阈能到250 MeV 的反应截面和弹性散射角分布实验数据,而获得一套参数比较少的新的3He 普适唯象光学势,对没有实验数据的反应截面和弹性散射角分布有一定的预言作用。论文第2 部分给出了光学模型势的一般公式,第3 部分给出了一套新的3He 普适光学模型势参数,第4 部分对于理论计算结果和实验数据进行了比较,第5 部分是结论。
1 光学模型势
唯象光学势一般可以分为实部势、虚部势和自旋-轨道耦合势三部分,其一般形式可表示为:

其中,VR(r,E)为实部中心势,VS(r,E)为面吸收虚部势,WV(r,E)为体吸收虚部势,VC(r)为库仑势,VSO(r,E)为自旋-轨道耦合势的实部。
实部中心势为:

面吸收虚部势为:
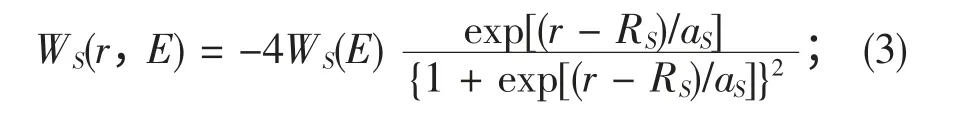
体吸收虚部势为:

自旋-轨道耦合势的实部为:

库仑势取为具有均匀电荷密度半径为RC的圆球的电势场,其形式为:

其中,z 和Z 分别是入射粒子和靶核的电荷数。式(6)中的几何半径参数为
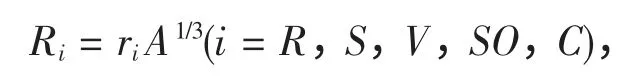
这里A 为靶核的质量数;ai(i = R,S,V,SO)为弥散宽度;VR(E),VS(E),VV(E),VSO(E)是与能量相关的项。
此外,对复合核弹性散射角分布的计算都采用带宽度涨落修正的Hauser-Feshbach 理论。
2 3He普适唯象光学势参数
利用3He 与不同靶核反应的去弹截面和弹性散射角分布的实验数据以及光学模型程序APMN[7],获得了一套适合于靶核质量数20≤A≤209 和入射3He 能量从阈能到250 MeV 的普适唯象光学势。光学势中能量相关项的形式具体如下:
光学势的实部:

面吸收虚部势:
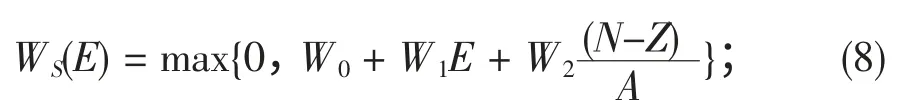
体吸收虚部势:

其中,Z,N,A 分别表示靶核的电荷数、中子数和质量数。E 是3He 在实验室系中的能量。 表1 给出了3He 普适唯象光学势参数。
表1 中aR,aS,aV,aOS分别是光学势的实部势、面吸收虚部势、体吸收虚部势、自旋轨道耦合势的弥散宽度,rR,rS,rV,rSO,rC分别是光学势的实部势、面吸收虚部势、体吸收虚部势、自旋-轨道耦合势、库仑势的半径参数,VR(E),WS(E),WV(E),VSO和E 以MeV 为单位,aR,aS,aV,aSO,rR,rS,rV,rSO,rC以fm 为单位。 表中的21 个参数有17 个是被调节的,其中参数V3,V4,W2和rC是常数,是基于Becchetti 和Greenlees[8]以及韩等人[9]的结果。

表1 3He 普适唯象光学势参数
把得到的3He 普适唯象光学势与现有的4 套3He 普适唯象光学势比较可以发现,它们都是用Woods - Saxon 势的形式,但是势的能量相关项有所不同。我们的普适唯象光学势在3He 入射能量100 MeV 以下与能量是线性关系,随着3He 入射能量的增加,在100 MeV 以上能量二次方项的贡献在增加,面吸收虚部势在3He 入射能量比较低的时候有贡献,体吸收虚部势在3He 入射能量20.0 MeV以上才有贡献;Becchetti 和Greenlees 给出的与Trost 等人给出的光学势都没有考虑体吸收虚部势的贡献;与庞等人的光学势比较,我们的势阱的深度、宽度和半径的依赖关系都与其不同,另一方面我们的光学势考虑了同位旋相关项的贡献;与梁等人的光学势比较,我们光学势参数的个数比较少。
3 理论计算结果与分析
为了验证唯象光学势的合理性,我们计算了不同入射能量3He 光学势随径向r(入射粒子和靶核的距离)的变化关系。 图1 和2 给出了3He 入射能量分别为20,50,100,150 和200 MeV,靶核为58Ni光学势的实部与虚部的径向关系,并且把唯象光学势的实部和微观光学势[10]的实部进行了比较。
从图1 中可以看出,光学势实部的深度随着半径和入射能量的增加迅速减小,并且这种趋势和微观光学势的计算结果是一致的,当3He 入射能量比较高时,唯象和微观光学势的实部的计算结果比较接近。

图1 不同入射能量3He 与58Ni 反应的唯象和微观光学势实部的径向关系
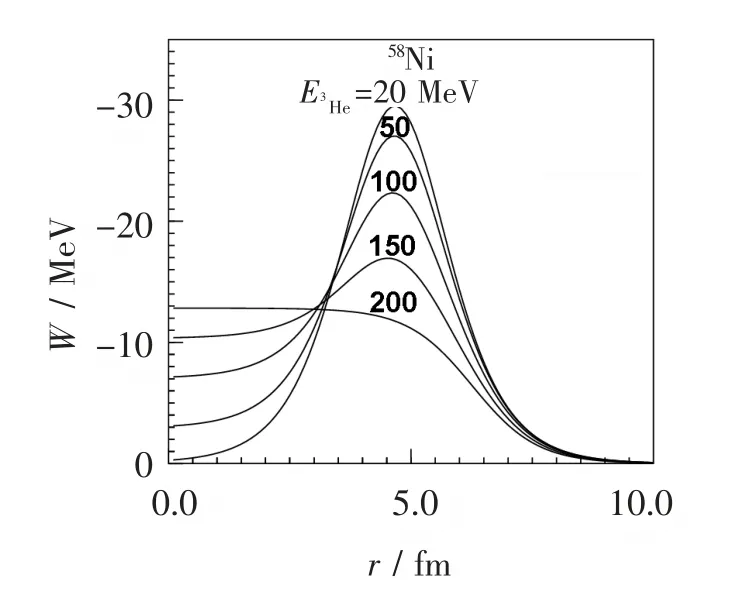
图2 不同入射能量3He 与58Ni 反应的唯象光学势虚部的径向关系
从图2 可看出,面吸收虚部势的深度随着入射能量增加而减少,而体吸收虚部势的深度随着入射能量增加而增加,当入射能量为200 MeV 时,面吸收虚部势已经很小,主要是体吸收虚部势的贡献。对3He 普适唯象光学势进行的物理分析表明得到的3He 普适唯象光学势符合物理规律,在物理上是合理的。
利用得到的3He 普适唯象光学势计算3He 入射能量在200 MeV 以下,靶核质量数从9 到208 的部分核的反应截面和弹性散射角分布,并与实验数据进行比较。
图3 是用3He 普适唯象光学势计算3He 与9Be,12C,16O,28Si,40Ca,58,60Ni,112,116,118,120,124Sn 和208Pb 反应的反应截面与实验数据[4]的比较。可以看出,除了12C 在入射能量96.4 和137.8 MeV 的理论计算结果比实验数据有点高,其余靶核的理论计算结果与实验数据符合得很好。另外,可以看到反应截面是随着靶核质量数和中子数的增加而增加,且总的趋势是随着入射能量的增加,重核的反应截面增加而轻核的反应截面是先增加后减小。对于同位素链58,60Ni和112,116,118,120,124Sn,反应截面随中子数的增加而增加,并且反应截面的理论计算结果和实验数据非常一致,这是由于在虚部势中引进了同位旋非对称项(N-Z)/A,这也进一步证明了我们的普适唯象光学势是合理的。
因为弹性散射角分布和反应截面数据有不同的敏感度,并且对于反应截面实验数据,光学势参数的选择非常敏感。面吸收虚部势WS 和体吸收虚部势WV 有限制的组合主要是用来描述反应截面。从图3 可看出,用我们的3He 普适唯象光学势能准确地描述反应截面,这结果表明,我们的3He 普适唯象光学势对于入射能量,靶核的质量数和中子数的依赖关系是合理的。

图3 3He 与不同靶核反应的反应截面理论计算值与实验数据的比较

图4 3He 与27Al 在不同入射能量下的弹性散射角分布与卢瑟福截面的比

图5 3He 与58Ni 在不同入射能量下的弹性散射角分布与卢瑟福截面的比
我们也计算了3He 与同一靶核在不同入射能量下的弹性散射角分布,并和实验数据进行了比较,其中所有的实验数据都是取自http://www-nds.iaea.org/exfor/exfor.htm.
图4 给出了3He 与27Al 在不同入射能量下的弹性散射角分布与卢瑟福截面的比的理论计算结果和实验数据的比较。从图中可以看出,除了在入射能量39.7 和46.0 MeV,且散射角度大于60°处的理论计算结果比实验数据小,其余入射能量的理论计算结果和实验数据符合得很好。
图5 给出了3He 与58Ni 在不同入射能量下的弹性散射角分布与卢瑟福截面的比的理论计算结果和实验数据的比较。从图中可以看出,除了在入射能量25.0 MeV 的理论计算结果比实验数据小,在其余入射能量的理论计算结果和实验数据符合得很好。
图6 给出了3He 与208Pb 在不同入射能量下的弹性散射角分布与卢瑟福截面的比的理论计算结果和实验数据的比较。从图中可以看出,用得到的3He 的普适唯象光学势去计算的弹性散射角分布与卢瑟福截面的比和实验数据符合得很好。

图6 3He 与208Pb 在不同入射能量下的弹性散射角分布与卢瑟福截面的比
4 结论
本论文通过符合大量的反应截面和弹性散射角分布实验数据获得一套适用于靶核质量数为20≤A≤209,3He 入射能量从阈能到250 MeV 的普适唯象光学势。理论计算结果和实验数据比较得到了很好的结果。得到的普适光学势能进一步试用于原子核模型的理论计算和实验分析中,例如在核天体物理中计算反应率或S 因子等。
[1]申庆彪. 低能和中能核反应理论[M]. 北京:科学出版社,2005.
[2]王书暖. 核反应理论[M]. 北京:原子能出版社,2007.
[3]Becchetti Jr F D,Greenlees G W. in Polarization Phenomena in Nuclear Reactions [M]. Madison:University of Wisconsin Press,1971:682.
[4]TrostH J,Lezoch P,Strohbusch U.Simple opticalmodeltreatmentofthe elastic3He scattering[J]. NuclPhys,1987,A462:333-375.
[5]Pang D Y,Roussel-Chomaz P,Savajols H R,et al. Global optical model potential for A =3 projectiles [J]. Phys Rev,2009,C79:024615.
[6]Liang Chuntian,Li Xiaohua,Cai Chonghai. Global3He optical model potential below 270 MeV [J]. J Phys,2009,G36:085104.
[7]Shen Qingbiao. APMN:A program for automatically searching optimal optical potential parameters in the E≤300 MeV energy region [J]. Nucl Sci Eng,2002,141:78 - 82.
[8]Becchetti Jr F D,Greenlees G W. Nucleon-nucleus optical-model parameters,A>40,E<50 MeV [J]. Phys Rev,1969,182:1190 - 1209.
[9]Han Yinlu,Shi Yuyang,Shen Qingbiao.Deuteron global optical model potential for energies up to 200 MeV [J]. Phys Rev,2006,C74:044615.
[10]Guo Hairui,Zhang Yue,Han Yinlu,et al. Helium-3 microscopic optical model potential based on the Skyrme interaction [J].Phys Rev,2009,C79:064601.
