改进的梯形公式及其代数精度
2013-01-17杨少华
杨少华
(1. 阜阳师范学院数学与计算科学学院,安徽阜阳236037;2. 辽宁大学经济学院,辽宁沈阳110036)
梯形公式是进行数值积分最为基础的公式之一,在解决一些数值积分的问题时起到不可替代的作用。因此,提高梯形公式在数值积分过程中的准确性成为研究的重点。 将从梯形公式余项“中间点”的渐进性入手,利用其渐进性定理对梯形公式进行校正,以得到代数精度较高的梯形公式[1]。

1 渐进性定理
定理1设函数f(x)在区间[a,x]上连续,在a 的某邻域内直到n + 3 次可导,且f(n+2)(a)≠0,则对于由
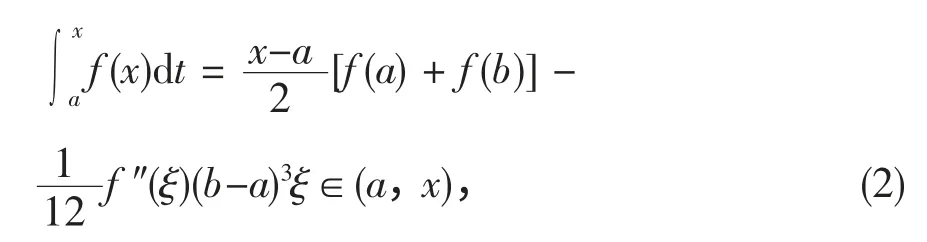
确定的ξ 有下式成立。

证明令

反复应用洛必达法则,得
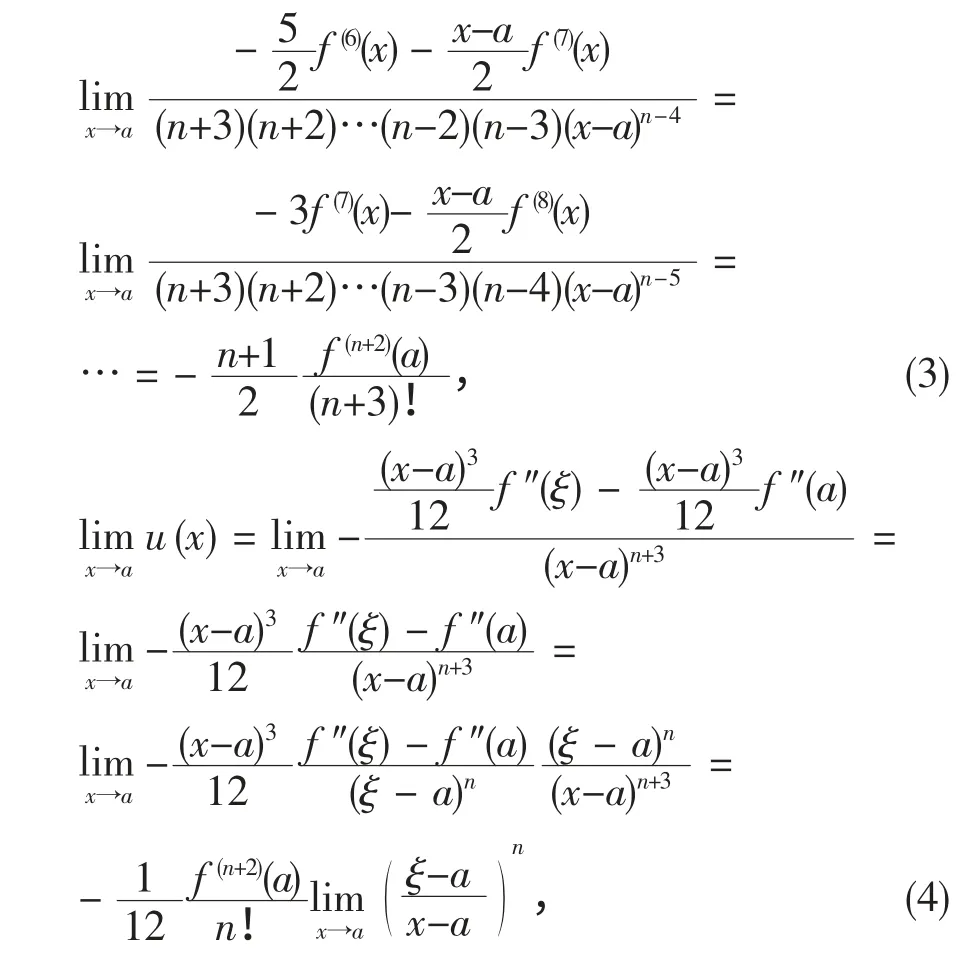
比较(3)式与(4)式,有

定理1 得证。
特别地,当n =1 时可以得到以下推论:
推论1设函数f(t)在区间[a,x]上连续,在a 的某邻域内直到4 次可导,且f‴(a)≠0,则对于由(2)式确定的ξ 有下式成立

证明 当n =1 时,利用定理1 的结论可得
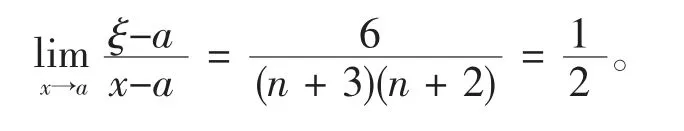
2 改进后的梯形公式及其代数精度
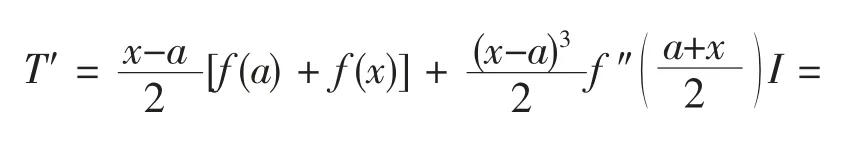
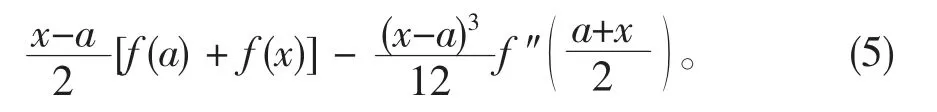
定理3设函数f(t)在区间[a,x]上连续,在a 的某邻域内直到4 次可导,且f‴(a)≠0,则校正后的梯形公式(5)具有3 次代数精度。
证明 不失一般性,考察a =0 的情形。
当f(t) =ti,i =0,1 时,

下面考察f(t)=ti,i =2,3 时的情形,把f(t)=t2,a =0,x =1 代入下式

有

把f(t)=t2代入(5)式,得

而
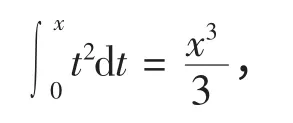

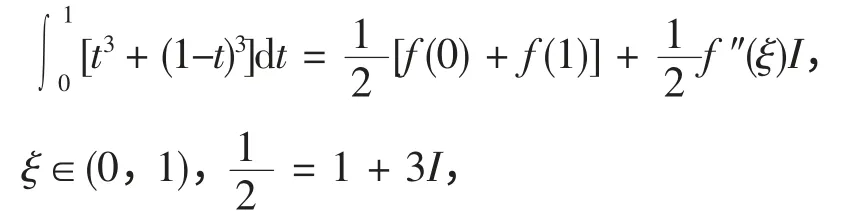
把f(t)=t3代入(5)式,得

而

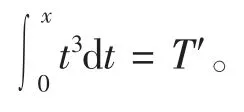
综上,校正后的梯形公式T′的代数精度为3,而梯形公式T 的代数精度为1[5],我们可以看到通过校正的梯形公式代数精度提高了2 阶。
[1]Bernard Jacobson. On the Mean Value Theorem for Integrals [J]. Amer Math Monthly,1982(89):300 - 301.
[2]李毅夫. 梯形公式余项“中间点”的渐进性定理及其应用[J]. 齐齐哈尔大学学报,2005,21(2):99 - 101.
[3]杨少华,华志强. Cotes 数值求积公式的校正[J]. 数学杂志,2012,32(4):644 - 648.
[4]杨少华. 辛甫生公式中间点的渐进性定理及其应用[J]. 贵州大学学报:自然科学版,2012,29(6):13 - 15.
[5]李庆扬,王能超,易大义. 数值分析(第4 版) [M]. 武汉:华中科技大学出版社,2006.
