基于FPGA的三电平风电变流器三维空间矢量调制算法

高 宁 罗悦华 王 勇 蔡 旭 ,2

（1. 上海交通大学电子信息与电气工程学院电力传输与功率变换控制教育部重点实验室 上海 200240 2. 上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室 上海 200240）

1 引言

三电平二极管中点钳位式变流器[1]（Neutral Point Converter，NPC）具有电压应力低以及输出谐波低等优势，并且能够用低压器件得到更高的输出电压，可有效提高系统效率，减小并网升压变压器的体积，是未来中压风电变流器的理想选择之一[2-4]。三电平中压风电变流器的拓扑结构如图1所示。

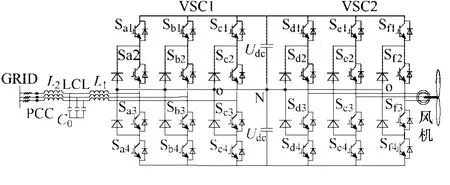
图1 三电平中压风电变流器系统拓扑Fig.1 Topology of three-level medium voltage wind power convertor

对于多电平风电变流器的控制算法而言，调制算法是极为重要的一环 ，直接决定了变流器的输出波形质量，对整机运行效果影响巨大。传统的三电平NPC的空间矢量调制算法计算比较复杂，而且随着电平数的增加算法复杂度成几何级数增加，在数字控制系统中需占用大量的 CPU资源。另一方面，在三相四线制系统的变流器中，由于指令电压存在零轴分量，需要在三维空间中进行矢量计算，称为三维空间矢量调制算法，由于空间坐标系的正交性，其运算量较传统SVPWM算法大为减少，关于此方面的研究已有大量积累[6-8]。而三电平 NPC的矢量空间结构的复杂度与三相四线制变流器类似，只是结构稍有不同，因此可将此类算法应用于三电平 NPC中。在文献[8]中，提出了基于三维坐标系的三电平NPC的数学模型，并基于此模型进行了三维空间矢量调制算法仿真，然而，该文只局限于仿真研究，未给出实验结果。在文献[9]中，提出了一种基于αβγ正交坐标系的三维空间矢量调制算法，由于αβγ坐标系事实上是对ABC坐标系进行旋转变换后的描述，因此显得不够直观，数字系统实现过程较为烦琐。本文对一种简化的基于 ABC坐标系的三维空间矢量调制算法进行了研究[10]，该算法非常适合于数字实现，本文将其运用于三电平风电变流器系统中，并在Altera公司型号为EP2C8的FPGA中进行了实现，最后在实验平台上进行了验证，证明了三电平三维空间矢量调制算法的正确性。

2 传统二维空间矢量调制算法[11-13]

传统的二维空间矢量图如图2所示，为简化文字，定义上下直流母线电容上的电压均为Udc。图2中，P代表+1，即对应的桥臂输出正直流母线电压Udc；N代表-1，即对应桥臂输出负直流母线电压-Udc；0则代表对应桥臂钳位至电容中点。二维空间矢量图共由27个矢量组成，可根据长短将矢量分为大矢量（如 PNN）、中矢量（如 P0N）和小矢量（如P00），整个αβ平面被分为24个小区间。二维空间矢量调制（2D-SVM）算法的所有计算均在αβ平面上完成，基本步骤可分为大小扇区判断，矢量作用时间计算，矢量发送三步，其中矢量作用时间的计算涉及大量非正交坐标系的运算，包括大量与相关的乘法运算。尽管有不少文献对 2D-SVM进行了优化，但总体而言，2D-SVM算法复杂度较高，在三电平风电变流器系统的应用中，需要对SVM算法进行改进。

图2 二维空间矢量图Fig.2 Vectors in two-dimensioned space

3 三维空间矢量调制算法流程

3.1 三维空间矢量坐标系的建立

由于αβ平面本身就是在三相对称前提下对三维空间的一种描述方法，因此，若将矢量放回到三维空间中进行描述，可以得到图3所示的三电平变流器的三维空间矢量图。

图3 三维空间矢量图Fig.3 Vectors in three-dimensioned space

其中，浅色线的平面即为αβ平面在三维空间中的描述，本质上 ABC-αβ变换即为三维空间中的矢量沿[1,1,1]方向投影至αβ平面上，因此三维矢量图能完整复现二维矢量图中的所有信息，比如大矢量、中矢量及小矢量的分类等，在三维空间中亦能描述清楚，反之将三维空间矢量沿[1,1,1]方向投影回αβ平面，亦能转化为二维空间矢量。观察图3，矢量在三维空间中组成一个大立方体，与2D-SVM中的六边形相类似，三维空间矢量调制算法（3D-SVM）的所有计算均在这个大立方体中进行。

考察三维空间的构成，Ua=Ub=Uc=0三个平面将整个空间分为八个卦限，大立方体被分割成八个小立方体，小立方体的数目与变流器的电平数相关。这些小立方体的内部空间构成完全相同，包含的八个矢量只相差一个直流分量，暗示了可以通过坐标原点平移的方法将八个小立方体化归一化到一个立方体中进行分析，正是这个特性，大大简化了3D-SVM算法。

3.2 3D-SVM理论分析

根据上述分析，3D-SVPWM算法的具体步骤如下[13]。

3.2.1 确定参考矢量所处的小立方体

如前面所述，三维空间矢量由八个小立方体组成，先要确定参考矢量落在哪个小立方体中方能进行下一步计算，如图4所示。

图4 相对坐标系原点确定Fig.4 The origin of relative coordinates

将输入电压按直流母线电压Udc进行归一化处理后按式（1）取整数部分（int表示向下取整），可得到所处小立方体的原点坐标，即小立方体中距离点 NNN最近顶点的坐标，该坐标表征了参考矢量的位置。由于小立方体内部空间构成的一致性，可以在每个小立方体内部建立一个相对坐标系以简化运算，相对坐标系的原点位于点（a,b,c），该相对坐标系内的所有矢量（即小立方体的顶点），均以（a或a+1,b或b+1,c或c+1）来表示。以图4中粗线所示参考矢量为例，该矢量位于左上角的小正方体内，因此a=0，b= -1，c=0。

3.2.2 确定参考矢量所处的四面体

每个小立方体又可以按照图5所示被其面对角面分为六个四面体，其中虚线表示用于分割立方体的对角面。由于三维空间坐标轴的正交关系，参考矢量所处四面体的判定将变得非常方便，最多只需要三次比较运算，而且不涉及乘法运算，如图5所示（由于作图视角的问题，图5c中的平面成一直线，下同）。

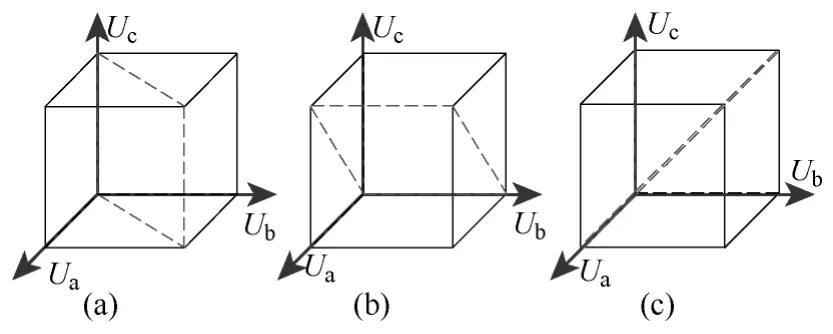
图5 小立方体的内部分割Fig.5 The division of sub-cube

3.2.3 确定矢量发送顺序

在确定了参考矢量所处的四面体之后，如图 6所示。根据3D-SVM中第一步和第二步的信息，按相电压输出在一个开关周期内只改变一次的原则，矢量发送顺序已经被唯一确定，以图6a为例，矢量发送顺序即为（a,b,c）→（a+1,b,c）→（a+1,b,c+1）→（a+1,b+1,c+1），矢量在以（a,b,c）为原点的相对坐标系中，从原点出发，沿着正方体的棱，每次移动长度为1（即Udc），最终到达顶点。

图6 矢量发送顺序示意图Fig.6 The sequences of vectors

3.2.4 确定矢量的作用时间

与二维空间矢量调制算法不同，3D-SVM算法的矢量作用时间计算非常简单，所有计算过程均由整数加减完成，不涉及到乘法运算，详细地计算过程将在后文的算法流程中给出。

3.3 3D-SVM算法流程

根据前面对算法原理的分析，判断矢量位置的算法流程图如图7所示，即前面的第一、第二步，该流程最多由一次取整和三次比较运算完成。

图7 矢量判断算法流程图Fig.7 Flow chart of vector judging

当矢量位置判断完成后，矢量发送顺序已被唯一确定，直接进行矢量分配时间的计算。根据伏秒平衡原理，可得到

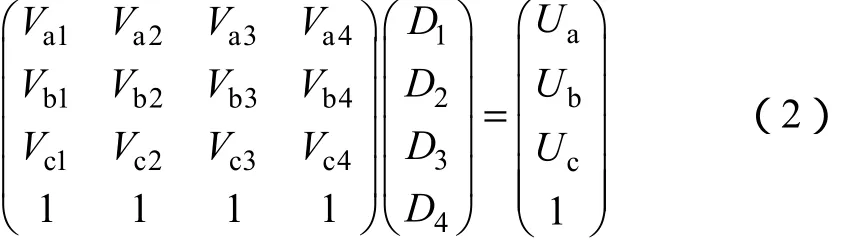
式中，Vxn表示在x相在第n个矢量作用时间内的输出电压，取值为-1，0或 1；Dn代表矢量作用时间占总开关周期的比例。

根据图6进行对上式分类求解，共有六种情况，结果列于表中，Case对应图中黑色圈内的值。

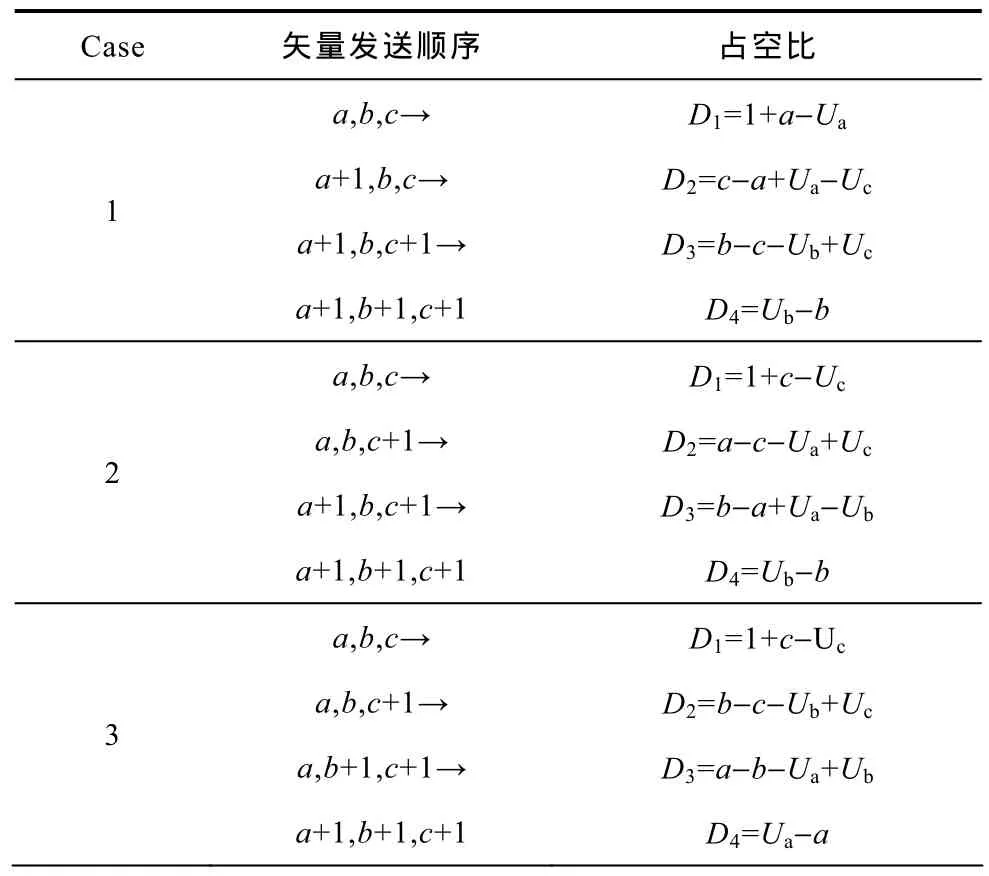
表 矢量作用时间Tab. The active time of vectors

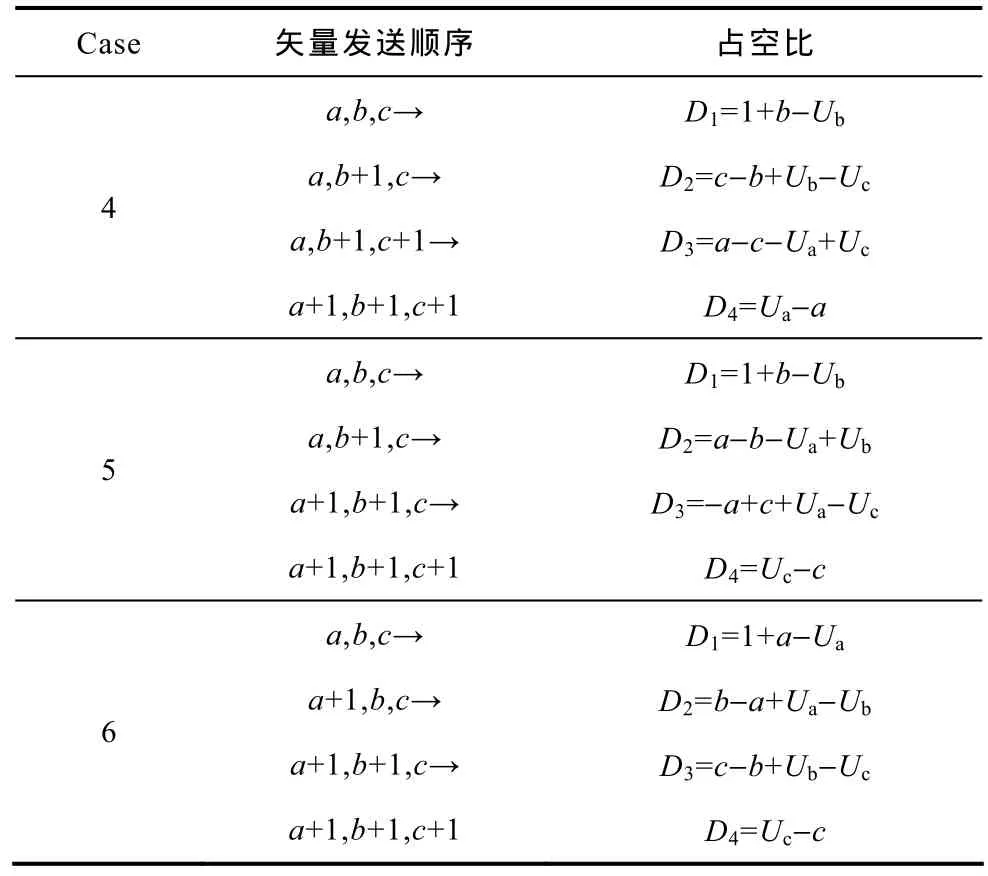
（续）

4 实验结果

4.1 3D-SVM的FPGA实现

由于3D-SVM算法全过程均由整数加减法和比较实现，因此很适合在FPGA中实现，可有机结合算法与硬件的优势。与传统取指令译码型的处理器不同的是，FPGA的使用非常灵活，在资源允许的前提下，可以将本来需要取指令译码串行执行的算法并行化，这样就可以极大的提高算法的执行速度。因此，针对一些高度重复的算法（比如调制，滤波算法），可以制作专用的FPGA模块来完成。根据算法流程，在FPGA中使用Verilog HDL语言实现了该算法。利用 Modelsim对算法进行时序仿真，仿真结果如图8所示。

图8 FPGA算法模块的Modelsim仿真结果Fig.8 Gate level simulation of 3D-SVM FPGA module in Modelsim

图 8中，DSP_Ua、Ub、Uc信号表示参考矢量的输入，从时序仿真中可以看出，从输入数据（即DSP_Ua信号的跳变沿，400.000ns处）到算法完成，得到矢量的占空比（422.824ns），仅耗时22ns左右，相对于主频为150MHz的处理器，视架构不同，一般22ns至多仅能执行数十条汇编指令。

在TMS320C6713+Cyclone II EP2C8的数字控制平台上验证了3D-SVM算法。由DSP产生正弦参考波，输入至FPGA中，由FPGA完成3D-SVM算法并产生门极脉冲。门极脉冲波形如下：其中IGBT管序号按图1中VSC1所示定义，高电平表示导通，根据图9a的结果，3D-SVM算法可以产生按正弦规律变化的三电平 PWM波，开关管在半个开关周期内保持常开/常关状态，而在另半个周期内高频开关，使变流器输出+Udc/0和 0/-Udc，证明了算法的正确性。将图 9a中的波形放大后可得图 9b，根据脉冲分析可得其矢量发送顺序为00N，P0N，PPN，PP0，符合最近三矢量合成的原则，其顺序与前文中人为选择的矢量发送顺序（表中的case6）一致。

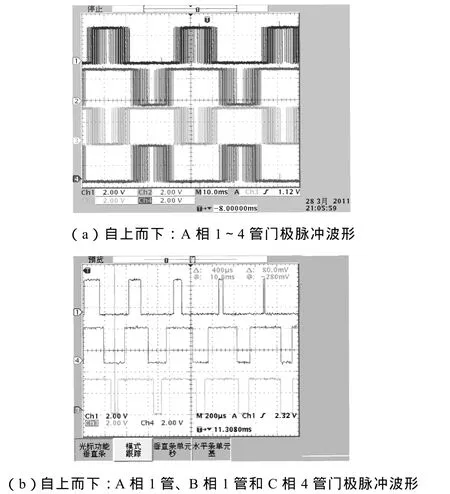
图9 3D-SVM门极脉冲波形Fig.9 Pulses generated by 3D-SVM

4.2 三电平风电变流器实验波形

为验证本文所述3D-SVM算法的正确性，将其应用于三电平风电变流器样机中，测量逆变器的输出电压，波形如图10所示，直流侧电压Udc为50V（总电压为100V），主处理器为TI公司的TMS320C 6713，辅处理器为 ALTERA公司的 EP2C8，所用IGBT模块为富士公司的2MBI150UH-33。所得实验结果列于图10。其中，图10a所示为变流器A相输出电压波形，工作调制比为0.9，其中CH3对应波形为输出相电压经过数字滤波后的波形。为验证3D-SVM算法的谐波特性，对其进行了详细地FFT分析，其中图10b为低频FFT谐波分析。根据图10b，30次以下谐波集中在3次、5次和7次（其中幅值最大的 3次谐波不出现于线电压中），根据波形计算，THD约为4.1%。图10c为高频FFT谐波分析，可见谐波主要集中于开关频率2.5kHz及其附近，由于是高次谐波，因此可通过滤波去除，对系统的电流总谐波含量影响有限。图10d给出了调制比变化为0.6的线电压输出波形。

图10 3D-SVM实验波形Fig.10 Experimental results based on 3D-SVM

5 结论

本文针对传统二维空间矢量调制算法的缺陷，将 3D-SVM算法运用于三电平 NPC风电系统中。3DSVM 算法避免了烦琐的非正交坐标系运算，减少了控制算法延时，对提高整机性能具有一定帮助。在三电平风电变流器实验样机上进行了试验，给出了FFT分析结果，输出相电压的THD（30次以下谐波）约为4.13%，输出谐波集中于开关频率附近，低次谐波的含量较少。实验结果表明了调制算法的正确性与可行性。

[1] Nabae Akira, Takahashi Isao, Akagi Hirofumi. A new neutral-point-clamped PWM Inverter[J]. IEEE Transactions on Industry Applications, 1981, 17(5):518-523.

[2] Amirnaser Yazdani, Reza Iravani. A neutral-point clamped converter system for direct-drive variablespeed wind power unit[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 596-607.

[3] 杨勇, 阮毅, 张朝艺, 等. 基于背靠背三电平电压变换器的直驱式风力发电系统[J]. 电网技术, 2009,33(18): 148-154.Yang Yong, Ruan Yi, Zhang Chaoyi, et al. Directdriven wind power generation system based on backto-back three-level converter[J]. Power System Technology, 2009, 33(18): 148-154.

[4] 张志, 谢运祥, 乐江源, 等, 消除中点电位低频振荡的三电平逆变器空间矢量脉宽调制方法[J].电工技术学报, 2011, 26(3):103-109.Zhang Zhi, Xie Yunxiang, Le Jiangyuan, et al.SVPWM method of removing the low-frequency oscillations of neutral point voltage for three-level NPC inverter[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 103-109.

[5] 翁海清, 孙旭东, 刘丛伟, 等. 三电平逆变器直流侧电压平衡控制方法的改进[J]. 中国电机工程学报,2002, 22(9): 94-97.Weng Haiqing, Sun Xudong, Liu Congwei, et al.Improvement on DC-voltage balance control method of three-level inverter[J].Proceedings of the CSEE,2002, 22(9): 94-97.

[6] Xiangsheng Li, Zhiquan Deng, Zhida Chen, et al.Analysis and simplification of three-dimensional space vector PWM for three-phase four-leg inverters [J].IEEE Transactions on Industrial Electronics, 2011,58(2): 450-464.

[7] 孙驰, 鲁军勇, 马伟明.一种新的三相四桥臂逆变器控制方法[J].电工技术学报, 2007, 22(2): 57-63.Sun Chi, Lu Junyong, Ma Weiming. A novel control method for three-phase four-leg inverter[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 57-63.

[8] Wu wenjun, Zhong Yanru, Duan Bo. A 3-D SVPWM without medium vectors for 3-phase 3-wire 3-level rectifier[C]. International Conference on Electrical Machines and Systems, 2008: 4199-4204.

[9] Nguyen T H , Paul K W Chan, Shrivastava Y, et al. A three-dimensional space vector modulation scheme for three-level three-wired neutral point clamped converters[C]. IEEE Power Electronics Specialist Conference, 2005: 2307-2314.

[10] Prats M M, Franquelo L G, Leh J I, et al. A SVM3D generalized algorithm for multilevel converters[C].The IEEE Annual Conference of Industrial Electronics Society, 2003: 24-29.

[11] 刘亚军. 三电平逆变器SVPWM控制策略的研究[D].武汉: 华中科技大学, 2008.

[12] 宋文胜, 冯晓云, 蒋威. 一种单相三电平中点钳位式整流器的 SVPWM 控制方法[J]. 电工技术学报,2007, 22(7): 69-73.Song Wensheng, Feng Xiaoyun, Jiang Wei. A SVPWM method for single phase three-level NPC voltage-source rectifier[J]. Transactions of China Electrotechnical Society, 2007,22(7): 69-73.

[13] Franquelo L G, Portillo R, León J I, et al. A 3-D space vector modulation generalized algorithm for multilevel converters[J]. IEEE Power Electronics Letters, 2009(4): 110-114.