风电并网引起电网电压波动的评价方法及应用

朱星阳 张建华 刘文霞 邱 威 吴 旭 蒋 程

（1.新能源电力系统国家重点实验室（华北电力大学） 北京 102206 2.国家电力调度控制中心 北京 100031）

1 引言

风力发电作为目前技术最成熟、最具规模的一种新能源利用形式，近年来在全世界得到了迅猛的发展，风电年均新增装机呈现快速增长。然而由于风力发电出力的随机性和弱可控性，大规模风电场并网将对电网的电能质量和系统安全稳定运行等诸多方面产生负面影响[1-5]，其中，电压问题是最突出和最受关注的问题之一。风速的随机变化将引起风电功率的随机波动，甚至风电机组的频繁启停，而功率的变化势必会引起电网电压波动。目前，风电场通常采用在风场出口母线上安装电容器组补偿风电场无功需求，这对风机启停造成的电压波动有一定的改善作用，然而，风机持续运行时风速或系统运行方式变化引起的风电场母线和接入点电压波动，难以通过简单的电容器或电抗器投切平抑[6]。另一方面，随着风机技术的发展，变速恒频机组逐渐成为并网风机的主流机型，虽然机组采用 PWM变频器控制实现有功无功解耦，具备动态调节无功输出的能力，从而可降低并网运行时对系统电压的影响，但由于种种原因，我国风电场中的变速恒频风电机组通常以恒功率因数方式运行，其快速灵活的无功调节能力并未得到充分的利用[7]。由此可知，对风电并网运行引起的电网电压波动进行全面准确的评价显得非常必要。

国内外学者对此进行了初探，形成了一些初步成果。例如，文献[8]对风电场接入电网引起电网电压偏差和电压波动的原理进行了分析，仿真表明风电场接入后，由于风速波动造成风电机组输出功率的波动会引起电压波动，其发出有功功率的大范围变动会造成整个运行区间较大的电压偏差。文献[9]对一个含风电容量较大的电网进行了潮流计算，根据历史记录的风速和风功率进行电网潮流的连续计算，来确定一年内由于风电场出力变化导致的母线电压和线路功率的变化，从而分析风电接入对电网电压的影响。文献[10]采用仿真方法研究了感应式和永磁同步两种风力发电系统在电网瞬间短路故障时系统电压波动情况，并对其进行了评估。文献[11]研究了风电场所接入电网状况对风电引起的电压波动与闪变的影响，指出系统短路容量和线路电抗与电阻比等对风电场的电压波动与闪变有较大的影响，通过选取合适的并网点和电压等级、合适的线路电抗与电阻比，能够有效抑制风电引起的电压波动与闪变。然而，以上文献本质上均是通过仿真的手段，研究风电接入后电网电压波动的相关影响因素，而没有对风电并网引起电网电压的随机变化进行全面评价。

基于上述分析，本文从电压随机分布的特征出发研究风电并网引起电网电压的随机波动，定义相应指标，给出评价方法。首先对风电场的静态模型进行了研究用于含风电场电网的潮流计算。然后，从电压波动的整体和局部两个方面分别定义电压分布指数、偏度指数、保持指数三个电压波动评价指标。最后，基于所提模型和评价指标，研究了采用蒙特卡洛抽样法对风电并网引起电压波动进行评价的方法及流程。通过仿真结果验证所提指标和方法的有效性、分析电压波动影响因素，并通过实例应用进一步说明指标和方法的实用性。

2 风电场静态模型

2.1 风速模型

风电机组出力的随机是由于风能的随机分布引起的，因此，研究风速的变化规律对于分析机组的出力变化及其对电网的影响十分关键。模拟风电场风速的方法很多，主要有时间序列分析法[12]、威布尔分布[13]和瑞利分布[14]。而对风速的大量实测数据表明，绝大多数地区的风速分布可以采用 Weibull分布函数描述：

式中，c和k分别为Weibull分布的尺度参数和形状参数。可通过下式求解得到

式中，μ、σ分别为各风速时段的期望和标准差。

2.2 风力发电机有功模型

风电机组有功出力与风速之间的关系可近似用图1所示的曲线描述。

图1 风功率模型Fig.1 Wind power model

计算时可以采用如下分段函数表示。

式中，vci为切入风速；vco为切出风速；vr为额定风速；Pr为风机额定输出功率。

2.3 风力发电机无功模型

本文以异步风力发电机和双馈风力发电机为代表研究风机在稳态分析中的无功模型。

2.3.1 异步风力发电机无功模型

异步风力发电机的简化电路如图2所示。

图2 异步风力发电机的简化等效电路Fig2. Simplified equivalent circuit of induction generator

图中U、P、Q分别为机端电压、有功、无功输出，xm为励磁电抗，xr为定子漏抗，rs为转子电阻，s为转差，xs为转子漏抗，忽略定子电阻。由图 2电路连接关系可以推导出

式中，x=xr+xs。

将式（5）变形得

将式（7）代入式（6）得异步风力发电机Q-U特性方程为

由式（8）知异步风力发电机吸收的无功Q是机端电压U的函数，故进行潮流计算时，将异步风力发电机母线按PQ（U）节点处理，即迭代过程中根据上一次电压迭代值不断更新风机的无功功率即可。

2.3.2 双馈风力发电机无功模型

由于双馈机组普遍采用了双 PWM变频器的控制，其发出的有功与无功功率能够得以解耦控制，具有类似于同步发电机的特性，在实际运行当中，其有功与无功都是可控的，所以在潮流计算时可以将双馈风电机组看作PQ节点，以简化分析。故以恒功率因数cosφ运行时，双馈机组无功模型为

2.4 风电场等值处理

大规模风电并网系统潮流分析时，若对风电场的每台风力发电机及其内部连接都采取详细模型描述时，不仅增加了电力系统模型的规模，而且还会带来数据修正、模型有效性等问题，增加计算分析时间。基于此，本文将风电场进行等值处理后再参与计算。风电场等值一般包含风速分布模型等值和发电机模型等值两方面的内容。本文暂不考虑风电场风速的分布情况，将同一风场中所有风机视为同一风速。发电机等值处理具体如下：

风场等值时，必须满足等值前后风场出口处的输出功率保持一致，即

异步发电机群采用容量加权法得到等效阻抗参数后再按式（8）参与潮流计算，容量加权法计算等效阻抗方法如下：

式中，ZΣ为等效发电机阻抗；n为被等值的发电机台数；Zj为第j个发电机阻抗；αj为容量加权系数；VAj为第j个发电机的额定容量。

与风力发电机直接相连的变压器，按阻抗并联等值处理，网络阻抗等值原则为等值前后网损相同，以保证潮流的等值前后一致。

3 评价指标

本文从描述风电并网后电网电压随机分布的特征出发，分别定义了电压分布指数、偏度指数、保持指数三个母线级电压波动评价指标，在母线级指标的基础上定义了相应的系统级评价指标。

3.1 母线电压分布指数

风电接入电网后，由于其出力随机波动，电网中母线节点电压也随之波动。图3为含大规模风电场的某地区电网中两条不同母线电压波动实际记录曲线。

图3 实际电网母线电压波动情况Fig.3 Bus voltage fluctuation in actual power system

由图3可知，风电并网引起电网不同母线的电压波动情况各不相同，直观表现为各时刻风电并网引起的电压偏移各不相同，而系统电压偏移程度是电压质量很重要的一个方面，系统电压偏移过大时，会影响工农业生产产品的质量和产量，损坏设备，甚至引起风机或风电场脱网等。更严重的是，在系统无功功率短缺、电压水平低下时，可能引起系统性的“电压崩溃”，造成大面积停电。可见，风电并网后引起电网电压波动幅度这一特征量非常重要。为此，采用电压观测值的标准差来表征某母线电压整体波动幅度情况，并将其定义为母线电压分布指数（Bus Voltage Distribution Index，BVDI）：

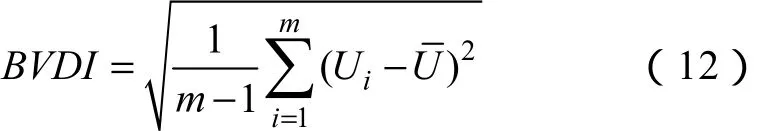
式中，Ui为第i次电压观测值，本文采用抽样计算得出；为电压平均值；m为抽样样本容量。

采用标准差衡量风电并网后引起电网电压的波动幅度，能反映波动幅度整体情况，可避免非风电波动的其他随机因素造成电压某一时刻瞬间波动的影响。从而使得评价具有全局性，结果更合理，更具有实际参考价值。

由母线电压分布指数的含义可知，BVDI值越大，表示风电接入后，电网母线电压分布越分散，波动幅度越大，对系统电压稳定越不利，电能质量也越差，反之亦然。

3.2 母线电压偏度指数

电压分布指数反映的是电压波动幅度，但没有反映风电接入后，母线电压相对于风电接入前增大或减小情况。事实上，在含风电场的电网规划或调度运行时，不仅需要预知风电并网引起母线电压的波动程度，还需要风电并网后母线电压提升或降低相关信息，以指导规划与调度运行工作，例如：配置合适的无功补偿器、电网运行时补偿器的合理投切。然而，由于风电出力是随机变化的，对系统中某一母线而言，风电并网后电压升高、降低均有可能，只是可能性有所不同。鉴于此，采用母线电压随机分布非对称程度来表征风电并网对母线电压提升或降低的相对影响程度。

在统计学中，经常采用偏度系数来表征分布偏斜方向和程度的度量。偏度系数一般有使用标准差和三阶中心矩两种计量方法。其中，使用标准差计量的定义式为

使用三阶中心矩计量的定义式为

SK是无量纲的量，取值通常在-3～+3之间，其绝对值越大，表明偏斜程度越大。当分布呈右偏态时，SK＞0，故也称正偏态；当分布为左偏态时，SK＜0，故也称负偏态。其几何含义如图4所示。

图4 统计学中偏度系数几何含义Fig.4 Skewness geometrical meaning in statistics

然而，使用标准差计量的定义适用于分组频数分布数据，否则式中的众数M0有很大的随机性。因此定义反映风电引起电网电压随机分布非对称程度的指标时，应参考三阶中心矩计量的方法。故定义母线电压偏度指数（Bus Voltage Skewness Index，BVSI）为

式中，Ui为第i次电压观测值；U0为在同种运行方式下风电接入前母线电压值；m为样本容量；σ为电压标准差。

BVSI值为正，表示风电接入后电压增大的情况比减少的情况严重，直观表示为电压分布概率密度曲线右侧尾部较长（以风电接入前电压值为基准），数值越大，右侧尾部越长。BVSI值为负，情况相反。当BVSI值为零时，表示风电接入后电压减少的情况与增大的情况相当，直观表示为电压概率分布曲线关于接入前电压值左右对称。

3.3 母线电压保持指数

指标BVDI和BVSI反映的都是关于电压分布的整体描述，没有反映母线电压维持在某数值的概率情况，事实上，这一信息可为电力系统的电压控制相关决策工作提供重要支持。因为与常规电力系统相比，风电并网后的系统电压随机性更强，相关的调度控制决策不能再依赖于确定性的准则，而需要进行概率决策分析。而状态保持概率分析是进行概率决策的重要方面，因此，定义一个表征母线电压维持在风电接入前电压水平的能力指标，并称之为母线电压保持指数（Bus Voltage Retention Index,BVRI）为

式中，C(Ω) 表示集合Ω中元素的个数，m为样本容量；α表示对电压波动范围的限制阈值，可根据评价需要自行指定。

由电压保持指数的定义可知，BVRI值实际反映的是风电并网后，母线电压维持在并网前的电压值附近的概率大小，指标值越大，表示对应维持概率越大，反之，概率越小。事实上，U0、α取恰当值时，BVRI也可反映出风电接入后母线电压合格率。

3.4 系统级评价指标

以上定义的BVDI、BVSI、BVRI指标均是母线级电压波动评价指标，下面定义几个对应的系统级指标。

系统电压分布指数（System Voltage Distribution Index, SVDI）：

定义式（18）～式（20）中，Ψ表示除平衡节点外的系统母线集合，N表示集合Ψ中母线总数。

系统电压偏度指数（SVSI）、系统电压保持指数（SVRI）、系统最大（小）电压偏度指数（MSVSI、NSVSI）、系统最大（小）电压保持指数（MSVRI、NSVRI）均类似定义。系统级指标用于对系统电压波动进行总体评价，以便对不同系统或同一系统不同规划、运行方案对比分析。

需要说明的是，由于风电并网对电网电压的影响范围与风电渗透率、电网结构、接入方案等诸多因素相关，为避免系统级指标过小而难以比较，必要时可结合实际情况或母线级指标计算结果，选择关键母线参与系统指标计算。

4 评价流程

结合本文研究的风电场静态模型以及所提指标，风电并网引起的系统电压波动评价流程如下：

（1）风电场等效：根据各风场所用的不同风机型号，依次参照 2.4小节对各风场风机进行等值，并计算各风场等值处理后的有功、无功出力额定值，异步等值风机只需得出如式（8）所示的无功出力表达式。

（2）风电场出力抽样：结合各风电场情况由式（2）、式（3）分别计算各风场风速Weibull分布的尺度参数c和形状参数k，根据式（1）产生各风电场风速抽样数据。

（3）潮流计算：将风速抽样值由式（4）转换为风电场有功出力抽样值，根据式（8）或式（9）得出风场对应无功出力，并依次进行潮流计算。

（4）指标统计分析：根据潮流计算结果统计得出母线电压分布指数BVDI，偏度指数BVSI，保持指数BVRI。

（5）根据BVDI、BVSI、BVRI各指标值，分析各母线电压波动情况，并得出SVDI、SVSI、SVRI等系统级评价指标。

具体评价流程如图5所示。

图5 评价流程图Fig.5 Evaluation flow chart

5 算例分析

5.1 系统说明

采用IEEE 36节点系统验证本文所提指标和方法的正确性和有效性。测试系统原始数据见文献[15]，本文对系统节点重新编号，如图 6所示。基准功率为100MVA，基准电压取11kV。

图6 IEEE 36节点系统Fig.6 IEEE 36 bus system

在节点18接入单机1MW、cosφ=-0.85双馈风电机组 5台；节点 33接入单机 1MW、cosφ=1双馈风电机组3台；两个小型风电场参数相同，具体见表1。

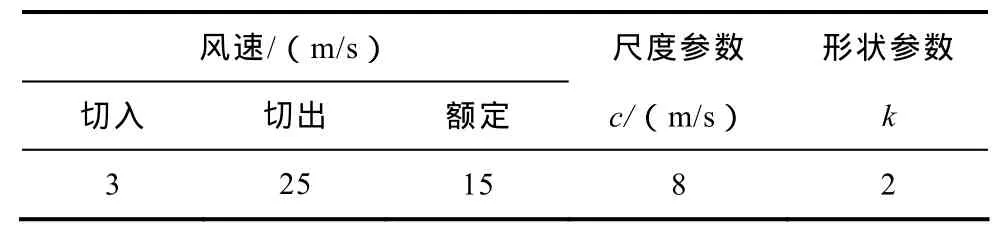
表1 风电场参数Tab.1 Parameters of the wind farm

5.2 结果分析与方法验证

由于风电接入规模较小，为便于分析母线电压保持指数BVRI，本算例中电压波动范围的限制阈值α取1%，在此条件下，各评价指标计算结果见表2。

表2 指标计算结果Tab.2 Results of index caculation

（续）

由表2可知：节点1～8、23～25的BVDI指标值相对较小，表明风电接入后其电压波动较小，而节点15～22、30～33的BVDI指标值相对较大，表明风电接入后其电压波动较大。这是因为节点 1～8、23～25靠近平衡节点1，由于平衡节点电压的钳制作用使得这些节点电压波动较小。而节点 15～22、30～33远离平衡节点且处于风电场接入点附近，故其电压波动大。由此可知，BVDI指标评价结果符合电网实际。

节点5～22的BVSI指标值为负，其他节点BVSI值为正。据电压偏度指数含义知，风电接入后，节点5～22电压下降情况更严重，而其他节点情况相反。结合两个风场的并网点位置和运行功率因数，分析可知BVSI指标计算结果符合实际。

图 7～图 9分别示出了节点 2、17、33电压分布概率密度（PDF）和累积分布曲线（CDF）。

图7 节点2电压分布情况Fig.7 Voltage profile of Node 2

图8 节点17电压分布情况Fig.8 Voltage profile of Node 17

图9 节点33电压分布情况Fig.9 Voltage profile of Node 33

经计算风电接入前节点2电压值为0.975 1、节点17为0.911 6、节点33为0.917 6。由图7可知，节点2电压概率密度曲线左右基本对称，电压升高（＞0.975 1）与下降（＜0.975 1）情况基本一致。由图8知，节点17电压概率密度曲线左侧尾部较长，电压下降（＜0.911 6）更严重。而图9中节点33电压概率密度曲线右侧尾部较长，电压升高（＞0.917 6）更严重。根据BVSI指标含义可知，图7～图9中节点电压分布特点与表 2中BVSI指标计算结果完全吻合，故所提指标BVSI能较好地反映风电并网后，母线电压相对于风电接入前增大或减小情况。

由表2可知，节点24～36的BVRI指标相对较小，而越靠近平衡节点的母线BVRI指标越接近于1，故在风电出力随机波动时，节点24～36的电压维持在风电接入前水平的概率相对较小，而其他节点维持概率相对较大，尤其是平衡节点附近的母线，由平衡节点的电压钳制作用可知这符合电网实际。故所提BVRI指标能准确反映风电并网后母线电压维持在接入前电压值附近的概率。

5.3 指标进一步说明

通过对比节点15～22和30～33的BVDI、BVRI指标，可以发现虽然这些节点的电压分布指数值均较大，而其电压保持指数却不同，节点30～33的电压保持指数较小，但节点15～22的电压保持指数仍较大。这是因为某些节点的电压整体波动范围虽较大，但存在局部密集分布的情况，图8中所示的节点 17的电压概率密度分布可证明这一点。由此可知，电压分布指数BVDI反映电压波动的整体信息，而保持指数BVRI主要反映电压波动的局部信息，两者不可互为替代。

5.4 指标影响因素分析

5.4.1 风电不同接入位置的影响

将 5台1MW、功率因数cosφ=-0.85的双馈风电机组依次通过IEEE 36网络的前段（节点4）、中部（节点11）、末段（节点22）并网，各母线电压偏度指数BVSI指标计算结果图10所示。

图10 不同并网点BVSI指标计算结果Fig.10 Calculation results of BVSI using different PCC

由图10知，通过节点4或22并网时，两种方案下各母线BVSI指标值均非常接近，但前一种并网方案各母线BVSI均大于0，后一种并网方案BVSI值均小于0，且在数值上几乎为前一种并网方案的2倍。这表明：风电在配电网络前段靠近电源侧或在网络末端接入，相对于并网前，各母线电压偏离程度基本一致；在靠近电源侧并网时，即使风电机组运行功率因数滞后时，仍有提升电网电压的可能；通过配电网末端并网时引起母线电压偏离程度较其他并网方案大，表 3中系统电压分布指数SVDI计算结果也表明了这一点。

表3 不同并网点SVDI计算结果Tab.3 Calculation results of SVDI using different PCC

由图10中通过节点11并网时各母线BVSI指标值可知，在网络中部并网时，引起电网各母线电压偏度程度各不相同，表现为接入点附近母线所受影响较其他母线大。

5.4.2 不同尺度参数c的影响

对 5.1小节所述风电场接入情况，取形状参数k=2，依次计算尺度参数c分别为5、8、12、15和20m/s时电网各母线级及系统级电压波动指标。表4示出了系统级指标SVDI、SVSI、SVRI计算结果。

表4 不同尺度参数系统指标计算结果Tab.4 System indexes for different scale factors

比较计算结果可知：随着尺度参数c增大，表征电压波动范围的系统级指标SVDI单调增大，系统电压保持指数SVRI先减小后增加；而系统电压偏度指数SVSI结果表明，随尺度参数c增大，系统电压总体上先上升，后降低，且降低程度呈强-弱-强的变化趋势。

不同尺度参数下风速概率密度曲线如图 11所示。

图11 不同尺度参数c时风速概率密度Fig.11 Probability density function of wind speed for different scale factors

由图11知，随着c值增大，沿横轴方向看，风速概率密度曲线峰值对应横坐标值逐渐增大，趋近于尺度参数，风速变化范围也逐渐增大，故系统SVDI指标值随尺度参数c增大而增大；沿纵轴方向看，风速概率密度曲线逐渐变平缓，且曲线峰值逐渐下降，小于切入风速vci的风速出现概率逐步减小，当c增至一定时，大于切出风速vco的风速出现概率也开始由0逐步增大，故电网保持风电接入前电压的概率先减小后增加，即电压保持指数SVRI先减后增。

在配电网中接入风电场对电压的影响考虑如下：一方面，有功的注入有利于提升电压水平，另一方面，若风场消耗无功，则会降低系统电压水平。故在风电场出力水平较低时，系统电压呈上升趋势，但风电出力增加到一定程度时，无功消耗的电压降低作用强于有功的提升作用，系统电压水平开始下降。在不同尺度参数下有效风速（vci≤v≤vco）出现概率呈如图12所示规律变化，故电压降低程度也相应表现为强-弱-强的非单调变化，从而，随风电场尺度参数c逐步增大时，SVSI指标按表4所示规律变化。

由表 4中SVDI、SVSI、SVRI指标的计算结果及对应分析可知，所提三个指标变化趋势无必然联系，这是因为三个电压波动评价指标分别从不同方面刻画风电并网引起的电网电压随机波动。事实上，这也体现了所提评价指标不冗余的科学性。

图12 不同尺度参数c时有效风速概率Fig.12 Probability of effective wind speed for different scale factors c

5.4.3 不同形状参数k的影响

对 5.1小节所述风电场接入情况，取尺度参数c=12m/s，依次计算形状参数k分别为1.8、2.0、2.2和2.4时电网各母线级及系统级电压波动指标。表5示出了系统级指标SVDI、SVSI、SVRI计算结果。

表5 不同形状参数系统指标计算结果Tab.5 System indexes for different shape factors

分析结果可知，随着形状参数k增大，系统SVDI、SVSI、SVRI指标基本不变，略呈下降趋势。不同形状参数k下风速概率密度曲线如图13所示。

图13 不同形状参数k时风速概率密度Fig.13 Probability density function of wind speed for different shape factors k

由图13中曲线变化趋势可知，表5中计算结果符合实际，验证了指标的准确性和有效性。

6 实例应用

将本文所提指标应用于指导某地区电网风电并网点优化。此系统电源总装机6 946.7MW，其中火电机组 6 800MW，地方小水电机组 146.7MW，均接入35kV及以下电网。电网最高负荷967MW，最低负荷390MW，220kV电网结构薄弱，呈单辐射链式结构，仅依靠2回220kV线路与省主网相连。网内仅有 220kV变电站，无 500kV变电站。据规划2012年末有550MW风电容量集中并入电网，风场位置如图14所示，现需对距离风电场分别为20km、17km、15km的三个220kV待选并网点NY、WN、SC的优劣进行综合比较。

图14 系统220kV接线图Fig.14 220kV system connecting diagram

方案评价时，在本文所提三个评价指标的基础上，再考虑并网后系统运行网损、并网线路建设成本，从系统网损率、线路投资、SVDI、SVSI、SVRI五个方面对并网方案进行综合评价。在电网典型运行方式下，对3个备选方案的五个考核指标分别进行计算，结果见表6。

表6 不同方案各指标计算结果Tab.6 Calculation results of indexes for different schemes

由表 6知，以上综合评价问题实质上是关于3个方案5个属性的多属性决策问题。此时可采用逼近理想方案的序数偏好方法（TOPSIS）[16]得到各方案的优劣排序。各属性取不同权重时，方案优劣排序决策结果见表7。

表7 TOPSIS决策结果Tab.7 TOPSIS decision results

分析表7知，随着对电压波动考察比重的逐步增大，方案WN、NY排序逐步前移，方案SC虽然投资较省，但其逐步被排为劣方案。典型运行方式下，不同并网方案时母线DF电压分布情况如图15所示，分析可知通过WN并网引起的电压波动较小，优于其他两种方案；通过 SC并网时，电压波动最大。这与表 7中各属性取不同权重系数的 TOPSIS决策结果吻合。

图15 不同并网方案母线DF电压分布情况Fig.15 Voltage profile of bus DF using different PCC

以上实例应用表明，所提指标能较好地反映风电并网引起的母线电压波动情况，可用于实际风电并网相关评价工作。事实上，所提指标还可用于指导风电并网方案改善、含风电场的电网网源协调规划等相关决策工作。

7 结论

本文从描述电压随机分布的特征出发，提出了风电并网引起电网电压随机波动的三个评价指标，并分别定义了对应的母线级和系统级指标，基于蒙特卡洛抽样给出了相应评价流程，方法简单可行。所提指标和方法具有一定实用性。算例测试结果表明，所提指标：电压分布指数、电压偏度指数、电压保持指数，能够较好地反映风电并网引起的电网电压波动情况，包括整体和局部信息。指标影响因素分析结果表明，风场并网点、风场尺度参数对电网电压波动影响较大，而风场形状参数影响较小。

本文所提指标仅从描述电压随机分布特征出发，反映风电引起电网电压波动信息是有限的，评价指标有待进一步扩充，以形成综合评价体系。

[1] 裴玮, 盛鹍, 孔力, 等. 分布式电源对配网供电电压质量的影响与改善[J]. 中国电机工程学报, 2008,28(13): 152-157.Pei Wei, Sheng Kun, Kong Li, et al. Impact and improvement of distributed generation on distribution network voltage quality[J]. Proceedings of the CSEE,2008, 28(13): 152-157.

[2] 邓卫, 唐西胜, 裴玮, 等. 含风电微型电网电压稳定性分析及控制技术[J]. 电工技术学报, 2012,27(1): 56-62.Deng Wei, Tang Xisheng, Pei Wei, et al. Voltage stability and control technologies of micro-grid with wind power[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 56-62.

[3] 迟永宁, 王伟胜, 戴慧珠. 改善基于双馈感应发电机的并网风电场暂态电压稳定性研究[J]. 中国电机工程学报, 2007, 27(25): 25-31.Chi Yongning, Wang Weisheng, Dai Huizhu. Study on transient voltage stability enhancement of grid-connected wind farm with doubly fed induction generator installations[J]. Proceedings of the CSEE,2007, 27(25): 25-31.

[4] 魏晓光, 汤广福, 魏晓云, 等. VSC-HVDC控制器抑制风电场电压波动的研究[J]. 电工技术学报,2007, 22(4): 150-156.Wei Xiaoguang, Tang Guangfu, Wei Xiaoyun, et al.Study of VSC-HVDC controller to mitigate voltage fluctuation caused by wind farm integration[J].Transactions of China Electrotechnical Society, 2007,22(4): 150-156.

[5] 陈宁, 于继来. 兼顾系统调频需求的分布式风电分散自治调控策略[J]. 电工技术学报, 2008, 23(11):123-130.Chen Ning, Yu Jilai. Strategy for decentralized autonomous regulation of distributed wind power considering system frequency regulation demand[J].Transactions of China Electrotechnical Society, 2008,23(11): 123-130.

[6] 曹娜, 赵海翔, 戴慧珠. 常用风电机组并网运行时的无功与电压分析[J]. 电网技术, 2006, 30(22):91-94.Cao Na, Zhao Haixiang, Dai Huizhu. Analysis on reactive power and voltage of commonly used wind turbines interconnected to power grid[J]. Power System Technology, 2006, 30(22): 91-94.

[7] 陈宁, 朱凌志, 王伟. 改善接入地区电压稳定性的风电场无功控制策略[J]. 中国电机工程学报, 2009,29(10): 102-108.Chen Ning, Zhu Lingzhi, Wang Wei. Strategy for reactive power control of wind farm for improving voltage stability in wind power integrated region[J].Proceedings of the CSEE, 2009, 29(10): 102-108.

[8] 黄学良, 刘志仁, 祝瑞金, 等. 大容量变速恒频风电机组接入对电网运行的影响分析[J]. 电工技术学报, 2010, 25(4): 142-149.Huang Xueliang, Liu Zhiren, Zhu Ruijin, et al. Impact of power system integrated with large capacity of variable speed constant frequency wind turbines[J].Transactions of China Electrotechnical Society, 2010,25(4): 142-149.

[9] Boehme T, Wallace A R, Harrison G P. Applying time series to power flow analysis in networks with high wind penetration[J]. IEEE Transactions on Power System, 2007, 22(3): 951-957.

[10] Hosaka N, Kumano T. Evaluation of voltage fluctuation in electric power system with wind power generators[C]. Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, 2008: 1-6.

[11] 吴义纯, 丁明. 风电引起的电压波动与闪变的仿真研究[J]. 电网技术, 2009, 33(20): 125-130.Wu Yichun, Ding Ming. Simulation study on voltage fluctuations and flicker caused by wind farms[J].Power System Technology, 2009, 33(20): 125-130.

[12] 潘迪夫, 刘辉, 李燕飞. 风电场风速短期多步预测改进算法[J]. 中国电机工程学报, 2008, 28(26):87-91.Pan Difu, Liu Hui, LI Yanfei. Optimization algorithm of short-term multi-step wind speed forecast[J].Proceedings of the CSEE, 2008, 28(26): 87-91.

[13] Bowden G J, Barker P R, Shestopal V O. The Weibull distribution function and wind power statistics[J].Wind Engineering, 1983(7): 85-98.

[14] Justus C G, Hargraves W R, Mikhail A, et al. Methods for estimating wind speed frequency distributions[J].Journal of Applied Meteorology, 1978, 17(3):350-353.

[15] 肖鑫鑫. 计及分布式电源的配电网潮流和短路电流计算研究[D]. 上海: 上海交通大学, 2008.

[16] Hwang C L, Yoon K. Multiple attribute decision making-methods and applications: a state-of-art survey[M]. New York: Springer-Verlag, 1981.