风力发电机组额定风速的选择研究

2013-01-15潘慧慧李永光

上海电力大学学报 2013年2期

潘慧慧，李永光

(上海电力学院能源与机械工程学院，上海 200090)

近年来，风能作为一种清洁、无污染的可再生能源，其技术的研发和应用发展迅速.在风电场建设中，风机选型过程是关乎投资和效益的重要步骤，而选择风力发电机组的参数尤为关键.其中，额定风速的选取对于风力机组的设计和风力发电机组的成本有非常重要的作用.

风力发电机组的额定风速是计算风力发电机组额定功率的依据，它决定了风轮直径等主要部件的几何结构尺寸，并将影响风机的制造成本和风力发电机组的整体性能.若该数值过大，机组将很少达到额定功率，降低了发电机的效率，提高了能量成本;若数值过小，将增大风轮直径，使得风轮及其辅助成本偏高.从额定功率来考虑，一般变桨距风力发电机组的额定风速与年平均风速之比约为1.7;而定桨距风力发电机组达到相同额定功率的风速要高一些，其额定风速与年平均风速之比为2.0 以上［1］.

林俊烈［2］以风力发电机组获得的年总发电量的最大值为目标，得出了额定风速与年平均风速具有非线性关系的结论.张海平［3］根据风速的Weibull分布，推导出了额定风速与Weibull双参数c和K的关系式.以上研究仅是以风资源状况为基础，没有考虑到额定风速对风轮直径和风机成本的影响.本文以充分利用风资源为原则，研究了额定风速对额定功率、年发电量、叶片几何尺寸，以及机组成本的影响情况，为风力发电机组额定风速的选择提供了科学依据.

1 风速的分布规律

描述风速的数值分布模型主要有双参数威布尔分布、三参数威布尔分布、瑞利分布等.其中，双参数威布尔曲线最符合风速统计分布规律［4］.它属于单峰的正偏态分布函数，其概率密度函数为:

式中:k——形状参数;

c——尺度参数，m/s.

在实际应用中，一般依据风速统计数据来确定威布尔参数值，进而求取平均值风速及其标准方差σ，表达式为:

依据威布尔分布的均值和方差近似关系式，可以得出:

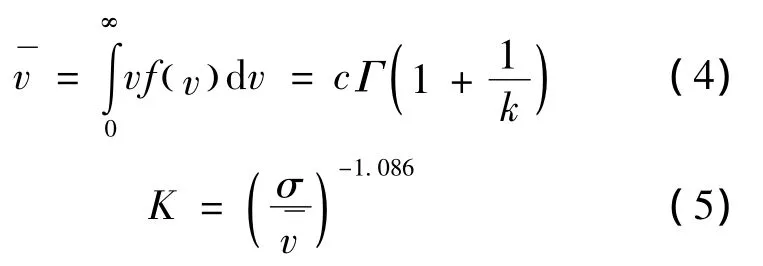
2 额定风速的相关因素

目前，普遍采用的确定额定风速的方法可以表示为［3］:

2.1 额定风速和额定功率的关系

风力发电机组的额定功率为［5］:

式中:ρ——空气密度;

A——风轮横扫面积;

Cp——风能利用系数.

由式(7)可知，额定功率与额定风速的3次方成正比，另外还与当地的空气密度、扫风面积、风能利用系数有关.

2.2 额定风速和风轮直径的关系

若已知一台效率为η，风轮直径为d的风机，其额定功率为:

风轮直径与额定风速的关系为:

由式(9)可知，适当提高额定风速，可以减小风轮直径.但随着风轮直径的增大，轮毂重量也会增加，其安装难度和费用也会增加.

2.3 额定风速和理论年发电量的关系

若已知当地风速的威布尔分布函数，全年有效风速小时数为T，单台风力发电机组全年的理论发电量为:

将式(1)代入式(10)，整理后得:

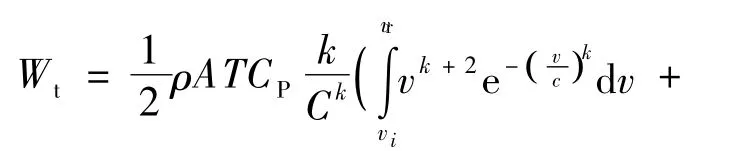
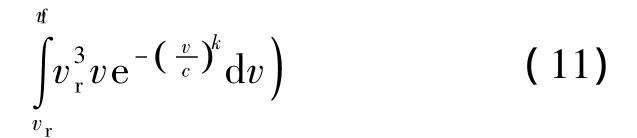
式中:vi，vr，vf——切入风速，额定风速，切出风速.

若某地区的风速分布已知，形状参数k和尺度参数c为常数，切入、切出风速一般情况下也为定值.当风轮直径一定的风力发电机组，其效率为η时，实际年发电量可以表示为:

由式(12)可知，年发电量与风速特性和风机各参数有直接关系，而与额定功率没有必然联系.

2.4 额定风速和机组成本的关系

FINGERSH L等人［6］提出，风轮造价 y(元)与叶片半径r(m)成指数关系，可以表示为:

由式(13)可知，适当提高额定风速，可以减小风轮直径，从而降低造价.

3 确定额定风速的工程实例

本文所研究的区域位于内蒙古自治区乌拉特后旗乌力吉苏木附近，风电场中心西距乌力吉苏木约19 km，东距旗府赛乌素镇约27 km，西南距海力素约28 km，海拔高度约为1 630 m.选用1#测风塔2006年9月1日至2007年8月31日完整性较好的连续一年的测风数据，对该地区的风况进行分析.

风电场70m高度测风年测得的月平均风速、风功率密度分布状况如表1所示.

表1 70m高度测风年测得的逐月平均风速及风功率密度

风电场70m高度测风年测得的全年风向频率和风能频率如表2所示.

由计算得到该风场各高度的风速频率分布Weibull模式拟合参数c和k，如表3所示.

该地区风能资源丰富，对照风电场风能资源评估方法(GB/T 18710—2002)中风功率密度等级表，本风电场风功率密度等级属4级.70 m高度年平均风速为8.0 m/s，全年平均风功率密度为486.6 W/m2，有效风速小时数为7 898 h(3～25 m/s);10 m高度年平均风速为6.2 m/s，全年平均风功率密度为224.1 W/m2，有效风速小时数为7 786 h(3～25 m/s).

表2 70m高度测风年测得的全年风向和风能频率

表3 各高度Weibull分布曲线参数

所拟选用的风力发电机组轮毂高度集中在65～70 m，则额定风速按式(6)计算可得:

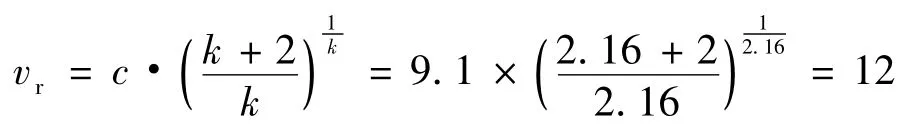
不同额定风速与满负荷小时数的关系如图1所示.

由图1可知，随着额定风速的增加，达到满负荷的小时数逐渐减少.

假设风机的切入风速为3 m/s，切出风速为25 m/s，风能利用系数为0.4，风机的运行效率为0.6，当地空气密度为 1.04 kg/m3.将上述各参数代入式(9)、式(12)及式(13)，计算得到不同额定风速时的风轮直径、年平均上网电量，以及叶片的价格，如表4所示.

由表4可以看出，降低额定风速，需要增加叶片半径.叶片越长，运输转弯半径要求越大，而对项目现场的道路宽度和周围障碍物的要求也越高.另外，起吊重量越大的吊车本身移动时对桥梁道路要求也越高，租金也较贵［7，8］.总之，生产成本和运输成本将显著增加，同时也提高了工艺难度.

图1 额定风速和满负荷小时数的关系

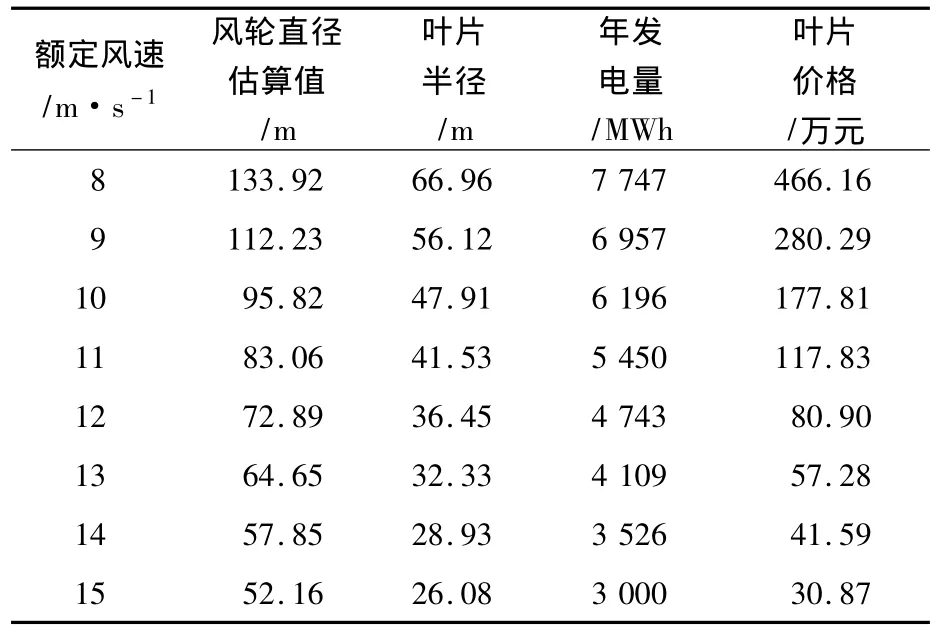
表4 不同额定风速下的各参数

表4中的计算结果表明，相同的单机容量，随着额定风速的下降，年发电量呈增大的趋势，并且年发电量与额定风速成线性关系.单从这一角度来看，相同的单机容量，额定风速越小越好，而综合考虑叶片的价格时，结论并非如此.

据资料显示，一般情况下叶片的成本占总成本的15% ～25%.假设1.5 MW风电机组的成本为600万元，则不同额定风速vr下叶片价格占总成本的比率如表5所示.

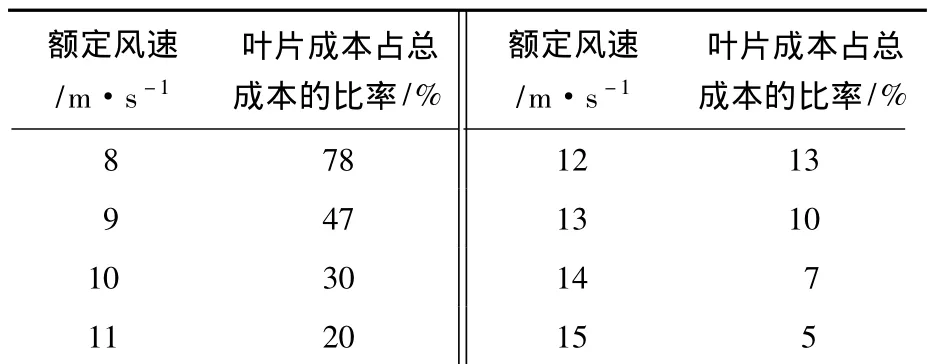
表5 不同额定风速下叶片价格占总成本的比率

由表5可以看出，额定风速为8～10 m/s时，叶片的价格占总成本的百分比已经超过了30%，这表明叶片成本过高，因此该范围内的额定风速不宜采用.本文取11 m/s为额定风速较为合理，叶片价格所占的比率20%在15%～25%合理范围内，而传统的方法计算得到的额定风速为12 m/s.由表3可知，额定风速为11 m/s与12 m/s相比，虽然叶片成本提高了36.93万元，但是每年的年发电量增加了707 MW，即提高了15%，大大增加了经济收益.

无论低风速资源区还是高风速资源区，都应综合考虑成本和发电量，对相同的单机容量，应尽量选择额定风速低的风机.尽管增大了叶片的半径，增加了成本，但发电量大大增加，总体来说，效益较好.