基于改进粒子群算法的电力系统无功优化

2013-01-15廖家平赵熙临

湖北工业大学学报 2013年2期

黄溥，廖家平，赵熙临

（湖北工业大学电气与电子工程学院，湖北武汉430068）

电力系统无功优化对于保证系统的经济性和安全运行有着重要作用，同时也是提高系统电压质量的重要方法.传统的无功优化方法主要是非线性规划法、线性规划法、混合整数规划法、动态规划法等，但这些传统的方法在应用上很难找到全局最优解［1］.因此通过大量的研究逐渐找到了一些更优的人工智能方法，主要包括：遗传算法、模拟退火方法、禁忌搜索、免疫算法［2］、人工鱼算法、蚁群算法［3］等.而粒子群算法是最近十几年才发展起来的一种新型的智能随机优化算法，该算法也已经成功地应用在电力系统的各个方面，包括无功优化、最优潮流计算、配电网重构、电网扩展规划［4］等.

1995年Kennedy和Eberhart提出了一种新型的随机搜索算法粒子群优化算法（Particle Swarm Optimization，PSO）.粒子群算法的优点在于容易实现、收敛速度快、具有较大的概率找到全局最优解；但是粒子群算法也存在一定的缺点，主要是容易陷入局部最优解，从而产生早熟现象；同时在算法的后期其收敛速度也比较慢.针对该算法的缺点，本文提出了对粒子群算法的一些改进以增强粒子群算法前期的全局寻优能力和后期的局部寻优能力.

1 无功优化的数学模型

1.1 目标函数

无功优化的目标函数主要包括技术性能指标和经济指标，本文以系统的最小网损为目标函数，如式（1）所示

其中：

公式（1）中第一项为网损值目标即系统的有功损耗；后两项则分别为PQ节点的电压和PV节点的发电机无功出力越限的罚函数项［5］.且

1.2 功率约束方程

功率约束方程即潮流方程为

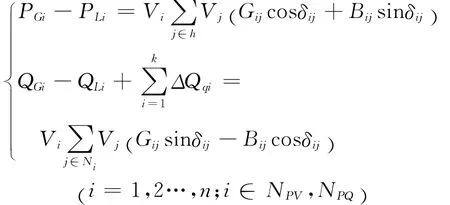
式中：PLi、QLi为负荷节点的有功功率和无功功率负荷；PGi、QGi为发电机节点的有功功率和无功功率出力；Qqi为节点i的无功功率补偿容量；Gij、Bij、δij则分别为节点之间的电导、电纳和电压相角差.

1.3 变量约束条件

变量约束分为控制变量和状态变量.控制变量分别为变压器的变比值Ti、无功补偿节点的补偿容量Cj、发电机端电压VGK；而状态变量则为节点电压Vj和发电机节点无功出力QGk.

控制变量的约束条件为

状态变量的约束条件为

式中：NPV，NPQ是PV节点和PQ节点的集合；NG，NT，NC是所有发电机节点、可载变压器节点及无功补偿节点的集合；Timax，Ti，Timin分别为可调变压器变比的上限值、实际值及下限值；Cjmax，Cj，Cjmin分别为无功补偿节点补偿容量的上限值、实际值和下限值；VGkmax，VGk，VGkmin分别为发电机节点端电压上限值、实际值及下限值；Vjmax，Vj，Vjmin分别为负荷节点电压上限值、实际值和下限值；QGkmax，QGk，QGkmin分别为发电机节点无功出力上限值、实际出力和下限值.

2 基本粒子群算法

在一个d维的目标搜索空间中，第i个粒子的位置Xi为（xi1，xi2，…，xid），第i个粒子的飞行速度vi为（vi1，vi2，…，vid） .记第i个粒子迄今为止发现的最好位置pi为（pi1，pi2，…，pid），整个粒子群体迄今为止发现的最好位置 pg为（pg1，pg2，…，pgd） .每次通过下面公式进行迭代来更新粒子的速度和位置以寻找粒子本身的个体最优解pi和整个粒子群的全局最优解pg.粒子寻优公式为

式中：w为惯性因子，一般取值在0.4～0.9之间；c1、c2为记忆因子，为非负的加速度常数，一般取值为2；r1、r2是两个独立的在［0，1］之间的随机数；vmin和vmax为空间中速度的最小值和最大值，一般根据实际应用自己设定.当＞vmax时，取＝vmax；当＜vmin时，取＝vmin.

3 对于粒子群算法的改进

PSO算法在应用中主要面临两个问题.一个是早熟问题，主要是种群中的粒子容易集中，从而形成种群的多样性损失过快；另一个就是算法后期收敛速度比较慢的问题.

3.1 对于早熟现象的改进

对于早熟现象的问题，设定一个阈值D，且

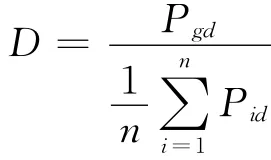
其中Pgd为种群中的全局最优解；Pid为第i个粒子在d维中的个体最优解；n为种群的规模数.

所以0＜D≤1，且当D越大种群中的粒子就越集中，越容易陷入局部最优解.对于阀值D设定一个最大值Dmax（0＜Dmax＜1），当DDmax时，就令种群中的一部分粒子重新初始化，这样就可以使粒子及时跳出局部最优，从而搜索到更好的全局最优解.

3.2 对于收敛速度的改进

针对PSO算法收敛速度的问题，改进其速度公式，新公式为

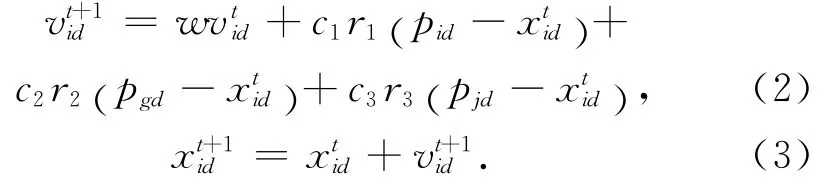
其中pjd为粒子种群中除粒子i外的任意随机一个粒子的个体最优解，这样添加的第三项不但能够增加PSO算法中粒子的收敛速度，同时也增强了粒子间的相互联系，特别是在算法的初期能够提高算法的全局寻优能力，而在后期也能够提高算法的整体收敛速度.

4 算法流程和算例分析

图1为本文算法的流程图.通过算法本身不断的比较、判定、迭代，最终在经过一定次数的迭代或者达到最终结果的要求后输出结果.一般在连续变量中可以直接采用迭代公式进行更新，但在电网无功优化问题中却需要对离散变量进行处理，所以在计算中本文采用映射编码和取整的方法对离散变量进行处理［6］.设粒子的位置向量即控制向量为X ＝（Ug1，Ug2，… ，UgNg，Qc1，Qc2，… ，QcNc，Tt1，Tt2，… ，TtNt），经过潮流计算，也可以得到与当前控制变量相对应的状态变量及输出变量，从而检验到是否满足约束条件.

图1 算法流程图

在仿真试验中（表1），以最小网损为目标函数，在节点系统中，包含2台发电机，2台可调变压器和2个补偿点［7］.在算法的计算中，设置粒子群的种群数m＝50，最大迭代次数Gmax＝200.优化后的MPSO算法结果通过与禁忌搜索算法、混沌优化算法和人工鱼群算法进行比较，从结果中可知：改进后的MPSO算法相对于另外几个算法具有更好的搜索能力.