水下航行体非定常空泡特性

田冠楠，孙龙泉，于福林，谢晓忠

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

水下航行体非定常空泡特性

田冠楠，孙龙泉，于福林，谢晓忠

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

航行体在水下高速运行时，其表面的局部低压区会产生空化现象，对力学性能有重大影响，空泡的不稳定性更使航行体表面的压力分布复杂。本文利用商用软件Fluent对轴对称航行体在水下高速运行时所产生的局部空化现象进行非定常模拟。通过Fluent软件的二次开发接口，引入更加合适的空化模型，并对RNG k-ε模型的涡粘性系数进行修正，通过与实验数据比较，验证方法的可行性。然后运用非定常方法实现对水下航行体肩部空泡初生、发展、脱落、溃灭等现象的模拟，揭示了空泡的周期性生长规律。通过观察空泡区流场流动规律及压力分布，研究发现空泡周期性脱落的原因。

航行体;二次开发;非定常空化;周期性

0 引言

航行体在水下高速运行时，由于绕流而使其局部表面压力降低，当压力降到低压区内的压力达到饱和蒸汽压力时，便产生空泡，即空化现象［1］。当空泡内的压力大于饱和压力时，空泡便会溃灭、脱落，在溃灭的同时将对航行体表面产生较大抨击力，对于物面结构有着较大影响，这也是剥蚀物面的主要原因之一［2］。因而空泡流的非定常特性是研究的前沿课题之一。

传统的研究空泡流的方法主要集中在应用试验上，然而这种模型试验耗时长、花费高。近年来，随着数值方法和计算机技术的提高，数值模拟方法已经成为研究空化现象的重要手段之一。基于求解Navier-Stokes方程的数值方法就可以考虑粘性情况下较好的模拟空化现象。Roohi［3］等应用VOF方法和LES湍流模型对二维水翼的定长空泡进行模拟，并与实验值对比，吻合较好。刘筠乔［4］等针对垂直出筒过程中通气空泡流进行研究，得到了在通气状体下导弹阻力系数的变化情况，研究了通气空泡的减阻特性。刘艳［5］等分别运用基于气泡动力学方程Rayleigh-Plesset方程推导而来的Singhal和Zwart-Gerber-Belamri空化模型，对于二维NACA66水翼进行研究，对比2种模型的准确性。

本文利用数值模拟软件Fluent，通过其自带的二次开发接口，运用UDF方法将基于液相体积分数的空化模型添加进入Fluent软件中，对轴对称型水下航行体进行数值模拟，研究航行体表面空泡的初生、发展、溃灭与脱落的整个过程，并对空泡脱落现象进行机理研究。

1 数学模型

1.1 控制方程

空化现象涉及到水、水蒸气两相，本文采用单一流体多种组分混合物模型，这种混合模型允许两相之间的互相掺混，对混合物建立基本方程包括连续性方程及动量方程［6］:

同时为了描述不同组分的比例关系，引入两相的体积比关系，流体中液相的体积分数用αl表示，气相体积分数则用αv=1-αl表示。针对体积分数的变化引入组分方程［7］:

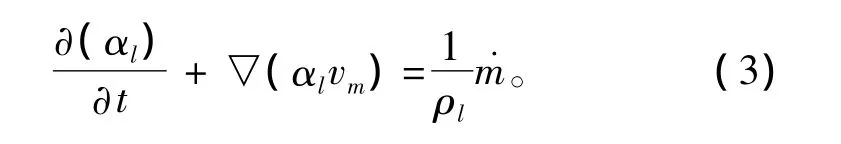
其中˙m表示单位体积从液相到气相的质量变化率。

1.2 空化模型

对于空泡流模型，在Fluent软件中，默认的是基于Singhal的全空化模型［8］，此模型一直被广泛运用于计算水翼、螺旋桨等绕流问题，但大部分都集中于分析定常问题的研究。在未对其修正之前，对于解决非定常问题，尤其是在模拟非定常空泡的脱落问题上具有一定的局限性，这主要与其自身的推导来源有关。其凝结率由Rayleigh－Plesset空气动力学方程推导得到:

从式(4)可看出，由于必须定义单位体积初生气泡的数量n，这就对仿真结果准确性产生一定程度的影响。本文采用KUN Z提出基于液相体积分数的的空化模型［9］，通过Fluent软件自带的二次开发功能，用C语言将空化模型导入 Fluent软件内。

该空化模型的相变过程受到液相体积分数αl和当地压力p与空化压力pv差值的控制。其中:Cd=Cp=100为凝聚和蒸发的经验常数;pv为空化压力;u∞为特征速度;t∞=L/u∞为特征时间。

1.3 湍流模型

本文采用RNG k-ε模型建立的输运方程，其关于k和ε的输运方程［10］:

为降低空化区内的粘性，达到更好的仿真效果，对涡粘性系数进行修正，引入函数f(ρ):

图1表示修正前后的粘性系数随密度的变化，从图中可知这种修正仅对混合区的粘性进行修正。

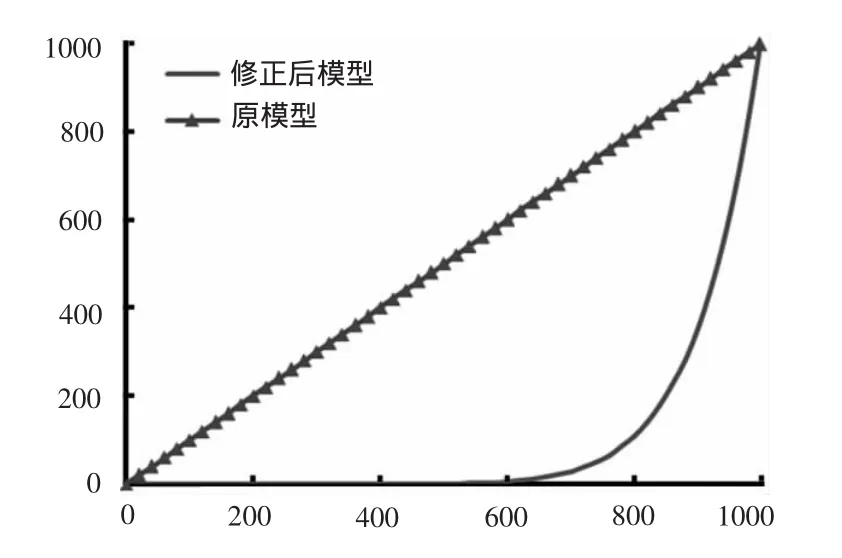
图1 修正前后的涡粘性系数对比Fig.1 Compared between pre and modified eddy viscosity

1.4 数值方法

通过有限体积法离散控制方程，对于空泡脱落现象的模拟采用隐式算子分割 (PISO)算法，该方法最初就是针对瞬态可压流动的无迭代计算所建立的一种压力速度计算程序，而后在稳态计算中也广泛的使用。这种算法相对于SIMPLE、SIMPLEC针对瞬态问题计算速度明显加快，更加适合应用于瞬态计算。

模型选择为半球头型轴对称航行体，轴径比为1∶5.5。整个模拟流场如图2所示，左侧入口采取速度入口，出口采用压力出口，中间为对称轴，上侧位固定边界，航行体表面采用无滑移壁面条件，侧壁采用滑移壁面条件。为较准确地模拟空泡脱落现象，对航行体表面的网格细化处理，如图3所示，贴近航行体表面的第一层网格Y+为1左右。

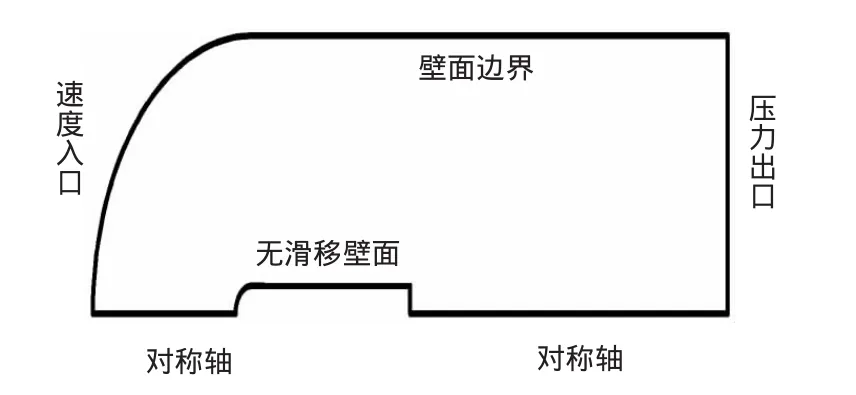
图2 计算流场及边界条件Fig.2 Computational flow and boundary conditions

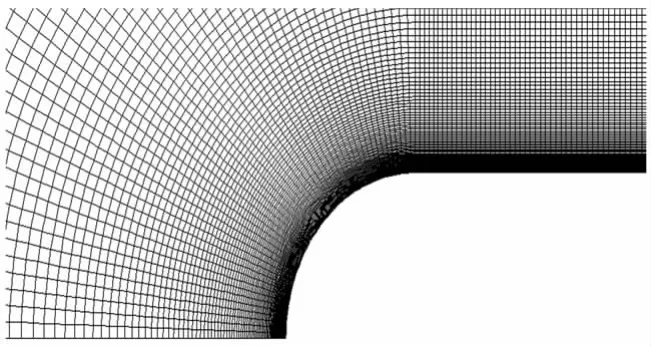
图3 头部网格分布Fig.3 Distribution of head grid

2 结果分析

2.1 航行体定常空泡流

首先针对半球头型航行体，分别在空化数为0.2，0.3情况下进行定常计算，得到沿航行体表面的压力分布。通过

获取航行体表面压力系数，并与实验值进行对比，如图4和5所示。图中横坐标为轴径比S/D，纵坐标为压力系数Cp。从图中可以看到对比较为吻合，随着空化数的降低，空泡长度有所增加。但在局部区域如空泡尾部有所差异，这主要是因为实验中不可避免的出现空泡扰动现象，而在定常计算中这种现象不明显。

图6绘制的是航行体头部表面的水汽云图，区域A和B表示的是水相体积分数。从图中可看出，在空泡尾部有明显的由于高压而产生的回射流现象。

图4 空化数为0.2的计算值与实验值对比Fig.4 Comparison of results with experimental resultsatcavitation number of 0.2

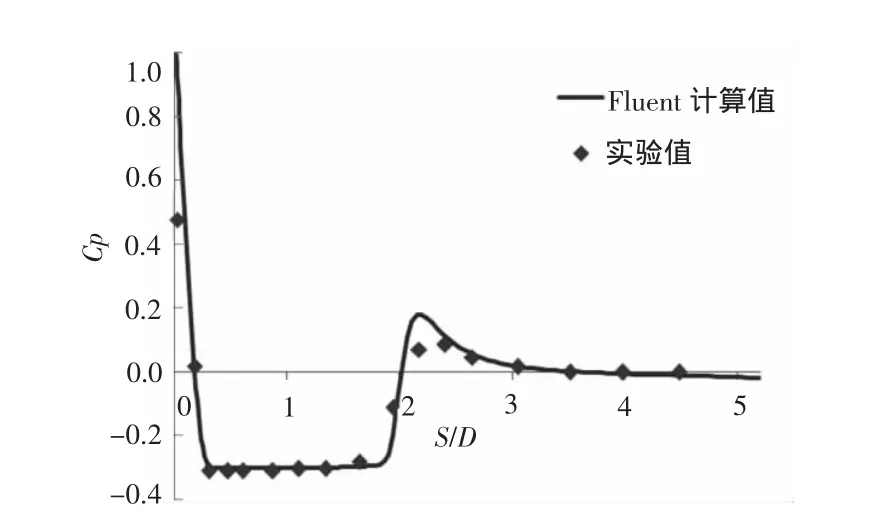
图5 空化数为0.3的计算值与实验值对比Fig.5 Comparison of results with experimental resultsatcavitation number of 0.3

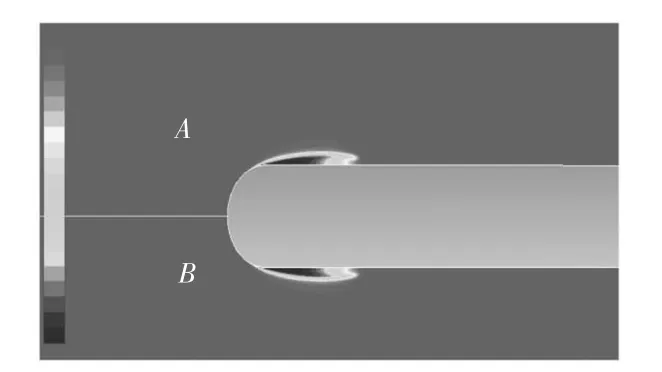
图6 航行体头部水汽分布Fig.6 Distribution of gas at head of vehicle

2.2 航行体非定常空泡流

这里同样针对半球型回转体，在空化数为0.4的情况下进行非定常模拟。图7为在各个典型时刻航行体局部空泡分布情况。

图7 典型时刻局部空泡分布Fig.7 Distribution of partial cavitation at typical moments

从图7可以清楚地发现在1个周期内航行体肩部空泡的整个发展周期。在初期，航行体由于肩部的形状变化而产生低压区，空泡随着时间变化而逐渐生长，当空泡长度达到最大长度后 (t=5/20T)，空化流场产生明显的与定常计算不同的特性，空化区域后侧逐渐产生断裂，并最后完全脱离 (t=11/20T)，同时断裂后空泡的脱落部分向后翻滚，产生较厚的空泡区 (t=14/20T)，最后完全溃灭在高压区。同时，头部的肩空泡也在生长，进入下1个周期。空泡经历了生长－脱落－溃灭－生长的周期性过程。

图8～图10是图7中圈出局部区域的速度矢量图，给出了几个典型时刻的速度矢量分布。其中数字代表密度等值线的标号。在初期，当空泡逐渐生长并达到最大长度后 (t=5/10T)，绕过空泡区的流体在空泡尾部速度迅速下降，形成的高压脉冲导致逆向流动，即回射流，并在空泡尾部形成漩涡，如图8所示。

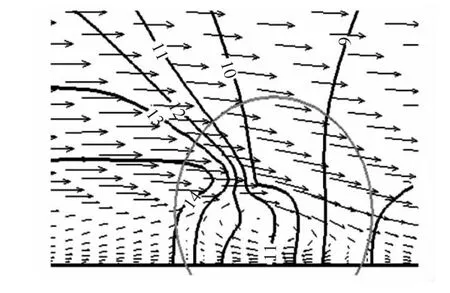
图8 t=5/20T时刻局部速度矢量图Fig.8 Velocity vector distribution at 5/20T

随后，空泡逐渐趋于一个相对稳定的阶段，只是逆向流动继续向前延伸，当发展到一定阶段时，这股回射流将空泡逐渐切断 (t=10/20T)，如图9所示。

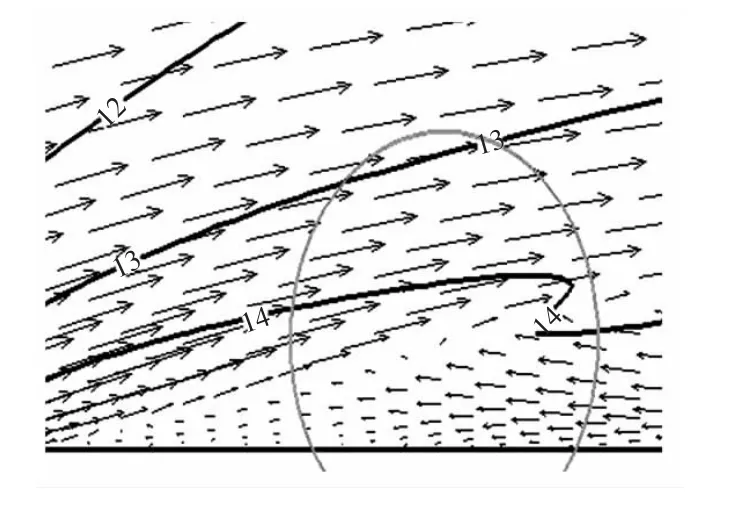
图9 t=10/20T时刻局部速度矢量图Fig.9 Velocity vector distribution at 10/20T

脱落后的空泡不断向后翻滚，堆积在一起，增加了后侧空泡的厚度，如图10所示，并最终在高压区溃灭。溃灭的空泡同时会产生较大的压力脉冲，如图11所示，这个高压脉冲对于航行体的力学性能有着较大影响。

图10 t=10/20T时刻局部速度矢量图Fig.10 Velocity vector distribution at 10/20T

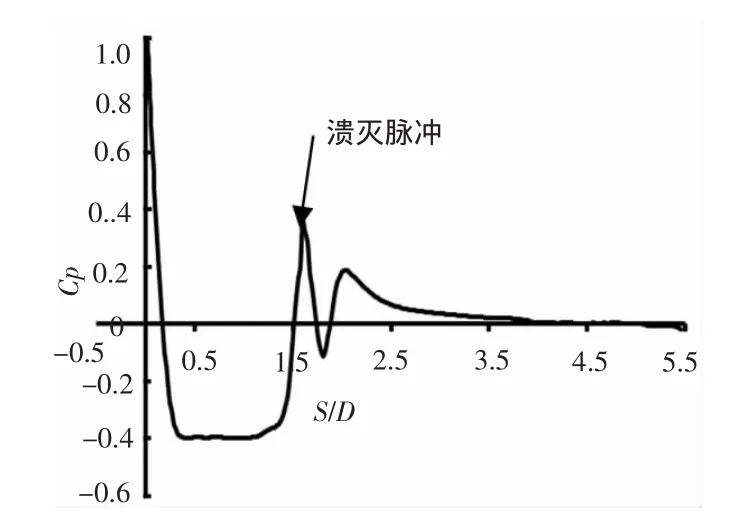
图11 空泡溃灭时刻航行体表面压力分布Fig.11 Distribution of pressure on the vehicle at the moment of collapse

3 结语

本文利用商业软件 Fluent，基于雷诺平均Navier-Stokes方程，通过Fluent的二次开发功能，引入基于液相体积分数的空化模型，同时对RNG k-ε输运方程进行修正，采用PISO算法的有限体积法，对在水下高速运行的航行体进行模拟。

利用这种方法能较为准确地模拟在定常和非定常情况下，航行体表面局部的空化现象，同时能够观察到航行体肩部空泡初生、发展、脱落和溃灭等周期性现象。通过对典型时刻速度矢量及压力分布的分析，高压脉冲导致的回射流是空泡脱落的主要原因。由于此方法在模拟空泡上体现出明显的优势，因此，应逐渐引用于三维有攻角的回转体研究上来，使其具有普遍意义上的工程应用价值。

［1］傅慧萍，鲁传敬，李杰．超空泡回转体减阻特性研究［J］．船舶力学，2004，8(3):31 －36．

FU Hui-ping，LU Chuan-jing，LI Jie．Numerical research on drag reuction characteristics of supercavitating body of revolution［J］．Journal of Ship Mechanics，2004，8(3):31－36．

［2］王志，陈九锡．回转体空泡绕流现象的数值模拟［J］．船舶力学，2006，10(4):38 －43．

WANG Zhi，CHEN Jiu-xi．Numericalsimulation of cavitation flow on revolution body［J］．Journal of Ship Mechanics，2006，10(4):38 －43．

［3］AMIR E R，ZAHIRI P．Numerical smulation of cavitation around a two－dimensional hydrofoil using VOF method and LES model［J］．Appl．Math．Modelling．2012，5(3):1－19．

［4］刘筠乔，鲁传敬，李杰．导弹垂直发射出筒过程中通气空泡流研究［J］．水动力学研究与进展，2007，22(5):549－554．

LIU Jun-qiao，LU Chuan-jing，LI Jie．An investigation of ven-tilated cavitating flow in vertical launching of a missle［J］．Journal of Hydrodynamic，2007，22(5):549 － 554．

［5］刘艳，赵鹏飞，王晓放．两种空化模型计算二维水翼空化流动研究［J］．大连理工大学学报，2012，52(2):175－182．

LIU Yan，ZHAO Peng-fei，WANG Xiao-fang．Study of cavit-ating flows around two-dimensional hydrofoil using two cav-itation models［J］．Journal of Dalian University of Technology，2012，52(2):175 －182．

［6］WATANABE T，KAWAMURA T，TAKEROSI Y，et al．Rhee S H．S-imulation of steady and unsteady cavitation on a marineprol-lerusingaRANS CFD Code［C］．Proceedings of 5th Internat-ional Symposium on Cavitation，Oska，Japan，2003:1 －8．

［7］LIU D，LIU S，WU Y，XU H．LES numerical simulation of cavitation bubble shedding on ALE 25 and ALE 15 hydrofoils［J］．Journal of Hydrodynamics，2009，21(6):807－813．

［8］SINGHAL A K，ATHAVALE M M，LI H Y．Mathematical basis and validation of the full cavitation model［J］．Journal of Astronautics，2007，28(6):1506 －1509．

［9］KUNZ R F，BOGER D A，STINBRING D R．A precoditioned Navier-Stokes method for two-phase flows with application to cavit-ationp［J］．Comput Fluids，1998，29:849 － 875．

［10］ ROUSE H，MCNOWN J S．Cavitation and pressure distribution head forms at zero angle of yaw，studies in engineering［Z］．Bulletin 32，State University of Iowa，1998．

The analysis of unsteady cavitation flow on underwater vehicle

TIAN Guan-nan，SUN Long-quan，YU Fu-li，XIE Xiao-zhong
(College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China)

The cavitation flow occurs on the partial low pressure areas of surface on the underwater vehicle，when the vehicle travels in high speed under the water．Especially the unsteady cavitation makes the distribution of vehicle complicated．The cavitation would have an important effect on the mechanical properties．With soft Fluent，the paper analysis the unsteady cavitaion flow on the ax symmetric vehicle．Applying the second development，the soft is added to fitter cavitation model．Besides，the eddy viscosity in the equation RNG k － ε is modified．Compared with the experiment，the result is proved well．Then the paper simulates appearance，growth，shedding，collapse of the cavitation flow successfully with the unsteady method．It reveals the periodic law growth．By absorbing the motion law and pressure distribution in the cavitation area，the paper gets the reasons of periodic shedding．

vehicle;second development;unsteady cavitation flow;periodic law

田冠楠(1989－)，男，硕士研究生，研究方向为流体力学。

TJ6301

A

1672－7649(2013)11－0015－05

10.3404/j.issn.1672－7649.2013.11.004

2013－01－04;

2013－01－15