发电厂不同机组间各班组小指标排名方法探讨

闫海行

(大唐鲁北发电有限责任公司 发电部，山东 滨州 251909)

发电厂不同机组间各班组小指标排名方法探讨

闫海行

(大唐鲁北发电有限责任公司 发电部，山东 滨州 251909)

指标竞赛是发电厂集控运作工作中的一项重点工作，小指标是一台机组整体性能的体现，也是运行人员操作水平的体现，同样是绩效考核管理系统的重要组成部分。由于发电厂不同机组间设备性能的差异，小指标得分不尽相同，甚至有很大差异，由于操作水平的不同，同台组不同班组间小指标得分也有较大差异。原则上讲，不同机组间的小指标得分是没有可比性的，但是有些时候需要把所有班组放到一起综合比较，这就给每个班组的指标得分排名带来了困难。本文在指标修正上提出了几种算法，试图寻找一种更为合理的办法，使不同机组间的小指标得分排名更为公平。

发电厂；集控运行；指标竞赛；绩效得分；指标修正；平均数；方差

0 前言

大唐鲁北发电有限责任公司成立于2009年3月25日，建设有两台330MW燃煤热电联产机组，分别于2009年9月21日和12月20日投产发电。指标竞赛是发电厂集控运行工作中的一项重点工作，由于两台机组设备性能的差异，造成绩效得分有所不同，1、2号机在整体上有很大差异，而且每个班组由于运行人员操作水平或设备运行状况的不同，绩效得分也有较大差异。因为绩效得分与个人奖金分配和岗位晋升有很大关系，这就给两台机5个值相当于10个班组的综合评价带来了困难。所以我们希望这个综合评价越合理、越公平越好，下文将就这个问题展开论述，寻找一种计算方法，使每个班组的排名更加科学合理。

1 平均数与方差的性质

（1）如果一组数据x1，x2，……，xn的平均数为x，方差为s2，那么一组新数据ax1，ax2……，axn的平均数为ax，方差是a2s2.

（2）如果数据x1，x2，……，xn的平均数为x，方差为s2，那么一组新数据x1+b，x2+b，……xn+b的平均数为x+b，方差是s2.

（3）如果数据x1，x2，……，xn的平均数为 x，方差为s2，那么一组新数据ax1+b，ax2+b，……，axn+b的平均数为ax+b，方差是a2s2.

2 指标修正

不同机组间的小指标得分差距很大，显然把每个班组实际的得分放到一起排名是不合理的，我们一般采取的办法是将一台机组的小指标得分修正一下再和另一台机组做比较，修正的原则是使两台机的平均得分相同，也就是每台机的总分相同。

以2013年4月份大唐鲁北发电厂两台机组的小指标得分为例：

1号机指标得分：一值16.18，二值14.14，三值14.25，四值16.82，五值15.83，平均得分15.45，方差1.14。

2号机指标得分：一值23.09，二值21.93，三值21.74，四值21.08，五值22.72，平均得分22.11，方差0.51。

两台机组的得分相差很大，显然直接给这10个数据排名是不合理的，一般情况下，我们把分数较少的1号机平均得分提高，使两台机组平均得分相同。我们将1号机和2号机指标得分命名为数组1和数组2。

2.1 算法一

计算两组数据平均数的倍数为1.432。即将1号机的指标得分乘以1.432，假设1号机原指标为x，修正指标为y，那么y=1.432x，可获得1号机五个值的修正指标：一值23.17，二值20.24，三值20.40，四值24.08，五值22.66。这五组数的方差是2.34。

2.2 算法二

计算两组数据平均数的差为6.67。即将1号机的指标得分加上6.67。假设1号机原指标为x，修正指标为y，那么y=x+6.67，可获得1号机五个值的修正指标：一值22.85，二值20.81，三值20.92，四值23.48，五值22.5。这五组数的方差是1.14。

2.3 算法三

按照上面的性质 3，已知1号机原数据平均数x=15.45，方差s2=1.14，求一组新数据y使y=ax+b，满足下列方程式：

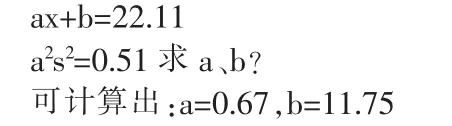
于是可获得1号机五个值的修正指标：一值22.61，二值21.24，三值21.31，四值23.03，五值22.37。这五组数的方差是0.51。

3 算法分析

第一种算法获得的数据方差为2.34，比原始数据的方差大了1.2，第二种算法获得的数据方差是1.14，与原始数据方差相同。这就是说第一种算法把1号机五个值之间的相对得分差距拉大了，使得分高的班组修正得分相对更高，得分低的班组修正得分相对更低。第二种算法缩小了第一名与第五名的得分差但却保持了原来的相对得分差距。因此算法二要优于算法一，它的波动性更小，数据更向平均数靠拢，在1号机五个班组间是相对公平的。

2号机各班组的得分数据方差是0.51，说明2号机运行人员水平更加平均，或者设备运行情况更加稳定。1号机经过修正后的数据方差后依然是1.14，远大于0.51，这说明1号机运行人员调整水平差距过大或者设备运行情况不稳定，过高的平均分差加在1号机数据上后，使1号机得分高的班组远大于2号机各班组，得分低的班组远低于2号机各班组，采取第一种算法甚至会使这个差距更大，这对2号机的各班组是不公平的。因此某台机组过高的得分差距会使前两种算法获得的修正数据对某些班组产生不公平。

产生这种现象的原因是修正后的1、2号机数据虽然有着相同的平均数，但方差不同。算法三就是使修正后的1号机数据与2号机数据既有着相同的平均数又有着相等的方差。将1号机修正后的三组数据和2号机的数据放到一组曲线中如下图所示：

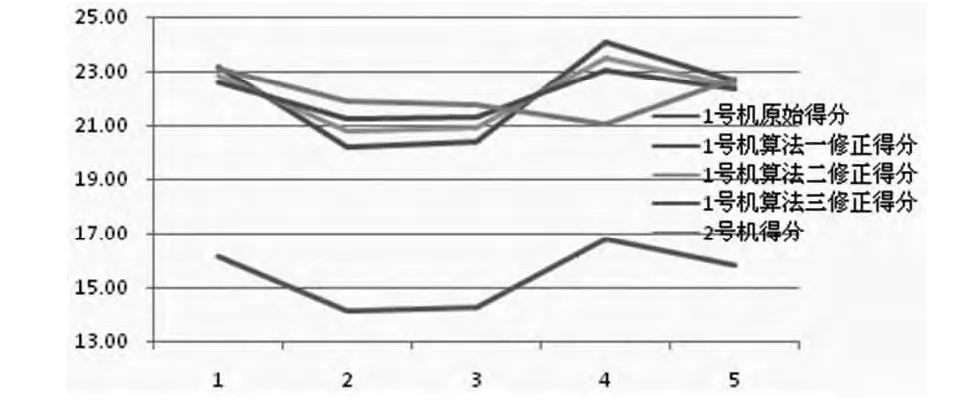
可以看出，算法三获得的修正数据相对算法一、二更为集中稳定，这种算法相对更加合理。

4 结论

没有绝对的公平，只有相对的合理。上述三种算法所得的得分差距很小，实际上，由于机组不同，根本没有一种完全公平的算法来解决这个问题。以上三种算法是以得分较高的2号机为基准的，如果取全年12个月的指标得分做比较，未必每个月都是2号机得分高或者方差小，如果1号机的得分方差小，也可以1号机为标准来修正2号机指标，而且这也是一种更为合理的做法。本文认为只要是两台机的得分数据平均数相同，方差相等，就是一种相对合理的比较。本文的算法同样适合多台发电机组间各个班组间的指标排名比较。

［1］宗序平.概率论与数理统计[M].2011-5-1.

汤静］