用极限的方法巧解中学数学问题*——以2012年高考数学题为例

梁双凤，何建锋

(楚雄师范学院数学系，云南 楚雄 675000)

极限方法是高等数学解决问题的最基本的方法，是建立高等数学的基石。新课程改革后，对中学生的数学运算能力要求，除传统的“加、减、乘、除”外，增加了“极限、求导”这些高等数学的基本运算，这说明极限已经成为现代人必备的一种解决问题的意识和策略。极限在实际生活与生产中最常规的表现形态是:极端位置或极端值。用极限的方法解决问题，就是从最特殊的位置、最特殊的点或者最特殊的值开始，探寻问题解决的一般方法和策略。

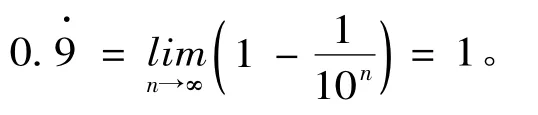
再例如，曲线的切线从它的定义到求出它的方程，始终都是用极限的方法和策略来完成的。如图1所示，曲线f(x)在点M处的切线就是割线MN的极限位置MT;而切线的斜率K=也是用极限的方法来定义和计算的。

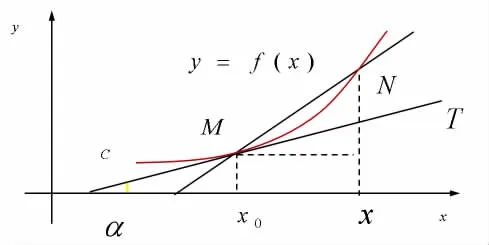
图1

同样，如果我们回顾一下渐近线的定义和求法也会发现，极限在其中扮演了不可缺少的重要角色。

除了按教科书里的定义来解释极限的涵义外，极限在实际生活与生产中最常规的表现形态是:极端位置或极端值。用极限的方法来解决问题，就是从最特殊的位置、最特殊的点或最特殊的值开始，探寻问题解决的一般方法和策略。

本文用极限的方法重新求解2012年全国及各省市的有关高考数学题，并以这些实例来说明，如何用极限的方法和策略来巧解不是极限问题的数学问题。

一、用极限的眼光，确定函数的图像

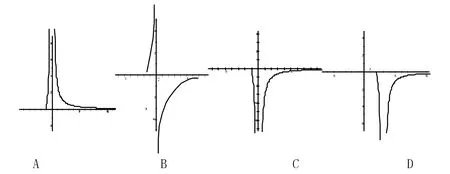
图2

分析 从提供的四个选项上，我们看到，这个函数的图像是由两支组成的，我们只需确定它们各自所在的位置，也就是它们各自所在的象限。

首先，由于函数的定义域为(－1，0)∪(0，+∞)，所以选项D被排除。

其次，探究当x∈(－1，0)时函数的图像。此时，我们研究函数在此区间的两个端点的极限，即

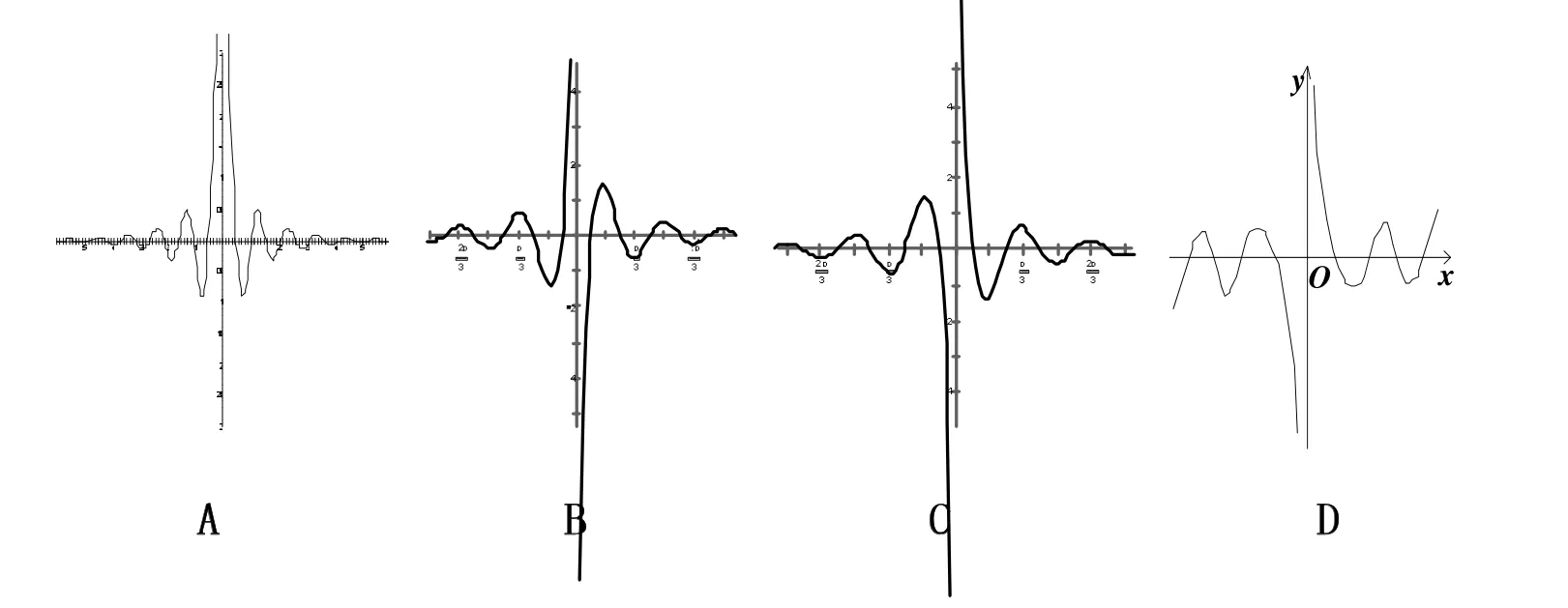
图3

分析 四个选项所提供的信息是:此函数的图像是对称图形。因此，可以由函数的奇偶性先进行判断:由于此函数是奇函数，故排除选项A。显然，我们只要考虑函数在(0，+∞)上的图像即可。

探究函数在(0，+∞)的图像，我们可以先考虑函数在区间两个端点的极限，即

二、用极限的手段，探寻参数的取值范围

例3 (12年全国卷第20题) 设函数f(x)=ax+cos x，x∈［0，π］;

(1)讨论函数f(x)的单调性;

(2)设f(x)≤1+sin x，求实数a的取值范围。

分析 此处我们仅仅探究实数a的取值范围。

如图4所示，它表示当x∈［0，π］时，直线y=ax－1始终要在曲线的下方;点A(0，－1)是直线与曲线的交点，且是曲线的最低点;在x=π处由aπ－1=1得于是过A(0，－1)，B(π，1)的直线AB:y=2x－1就是满足条件的π最上端的直线—极限直线。

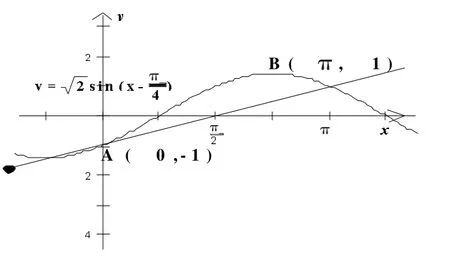
图4

图5

例4(12年全国卷第10题)已知函数f(x)=x3－3x+c的图像与x轴恰好有两个交点

分析 由于f(x)=x3－3x+c的图像与x轴恰好有两个交点，即方程x3=3x－c恰好有两个不同的实根，也就是曲线y=x3与直线y=3x－c恰好有两个不同的交点。

如图5所示，由于直线y=3x与曲线y=x3有三个不同的交点，上下平行移动直线y=3x就可得到直线y=3x－c;观察直线y=3x－c与曲线的交点个数，我们不难发现，只有当直线y=3x－c与曲线y=x3相切时，它们才可能恰好有两个不同的交点，即只有当直线y=3xc是曲线y=x3的切线时，才能满足条件。

由于y'=3x2，所以由3x2=3得切点为(1，1)或(－1，－1);由此可以得到与直线y=3x－c平行的切线的方程为y=3x+2或y=3x－2，从而得到c=±2。

回顾整个解题过程，我们可以看到，满足条件的直线y=3x±2，实际上就是最极端的直线，它是与曲线相交的最后的直线——极限直线。

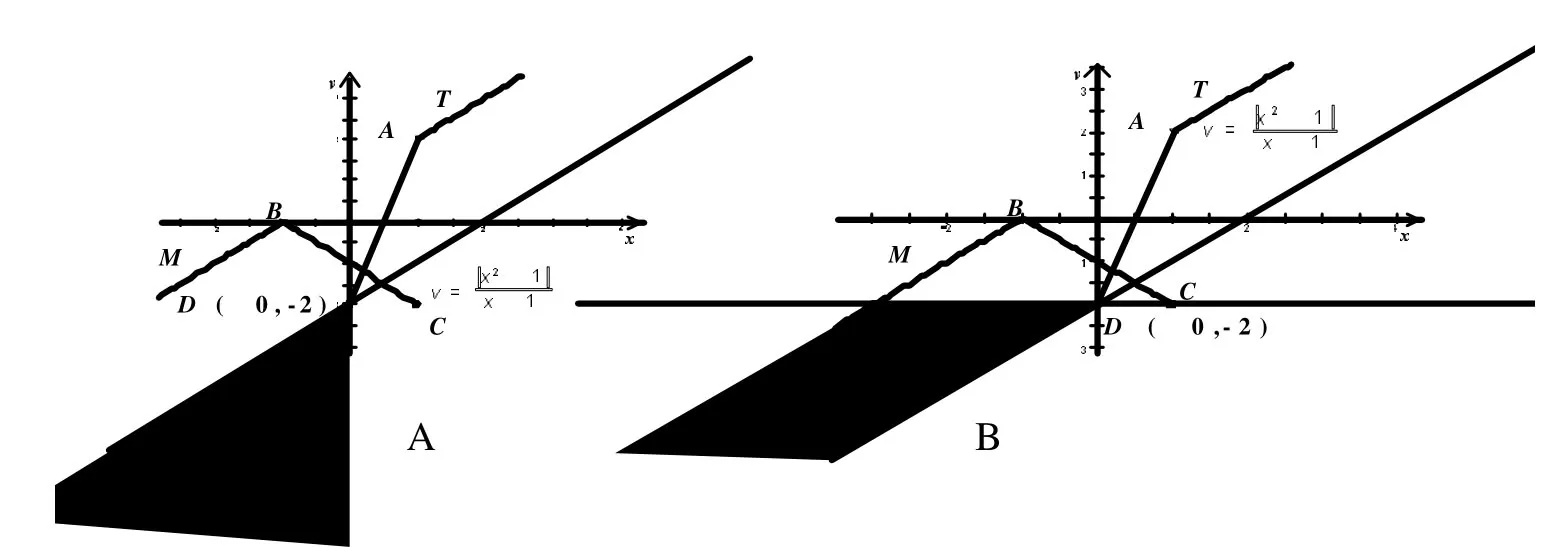
图6

首先，由于点D(0，－2)是动直线y=kx－2上的定点，我们先连接AD，则直线AD:y=4x－2就是当x→1时，满足条件的直线y=kx－2的最上端的直线，即极限直线。现在，我们把直线AD:y=4x－2围绕定点D(0，－2)按顺时针方向慢慢转动，此时，直线A'D始终保持与射线AT和线段BC各有一个交点;但当转动到直线A'D平行已知直线y=x+1时，即直线A'D的方程为y=x－2时，直线A'D就不再与射线y=x+1(x＞1)相交，即直线y=x－2是不满足条件的第一条直线，即极限直线(如图6A所示);由此，我们得到满足条件的参数k的取值范围:1＜k＜4。

其次，我们继续把直线A'D:y=x－2围绕定点D(0，－2)按顺时针方向慢慢转动，此时，我们可以看到，直线A″D始终保持与射线BM:y=x+1(x＜－1)和线段BC各有一个交点;显然，当直线A″D通过线段BC:y=－x－1(－1≤x＜1)的端点C(1，－2)时，直线DC:y=－2就是不满足条件的第一条直线，即极限直线(如图6B所示);由此，我们得到满足条件的参数的取值范围:0＜k＜1。

所以，我们得到满足条件的参数k的取值范围:0＜k＜1或者1＜k＜4。

例6(12年安徽卷第21题)数列{xn}满足x1=0，xn+1=－+xn+c(n∈N*)

(1)证明:{xn}是递减数列的充分必要条件是c＜0;

(2)求c的取值范围，使{xn}是递增数列。

分析 此处仅仅研究问题(2)。

数列{xn}是递增数列的充分必要条件是:xn+1－xn≥0(n∈N*)。

此式说明该数列有上界，从而当此数列是递增数列时，它必有极限。

三、用极限的策略，探究函数的最值

例7(12年课程标准卷第21题)已知f(x)满足f(x)

(1)求函数f(x)的表达式;

图7

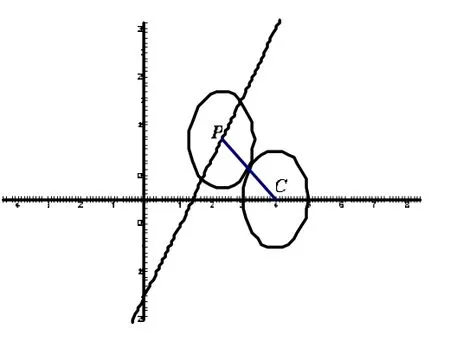
图8

令g(x)=ex，h(x)=(a+1)x+b;则有g(x)≥h(x)恒成立。它表示，曲线g(x)=ex始终在直线h(x)=(a+1)x+b的上方;如图7所示。由此我们知道，曲线g(x)=ex上一定存在一个点P(x，y)，使过此点的切线PT与已知直线h(x)=(a+1)x+b平行。

显然，此切线就是满足条件g(x)≥h(x)的最“高”直线，即极限直线。而由此所确定的直线，自然就是能使(a+1)·b获得极值的直线，即使(a+1)·b获得最值的直线。

因为g'(x)=ex，所以有ex=a+1，即x=ln(a+1)，从而得到切线的方程为

y=(a+1)x+(a+1)［1 － ln(a+1)］，由此得到 b=(a+1)［1 －ln(a+1)］;从而有(a+1)·b=(a+1)2［1 － ln(a+1)］。

令 a+1=t，则(a+1)·b=k(t)=t2(1 － ln t)。

由于 k'(t)=t(1 －2 ln t)，令k'(t)=0，则

即(a+1)·b=k(t)=t2(1－ln t)的最大值为

例8(12年江苏卷第12题)在直角坐标系xoy中，圆C:x2+y2－8x+15=0;若直线y=kx－2上至少存在一点使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值为____________。

分析 因为圆心P(a，b)在直线y=kx－2上，以P(a，b)为圆心，半径为1的圆与已知圆C有公共点，所以两圆心的连线CP不大于两半径的和，即|CP|≤2。由于点P(a，b)在直线y=kx－2上，所以，已知圆的圆心C(4，0)到直线y=kx－2的距离也不大于2，即≤2，解此不等式可得，从而得知k的最大值为

例9(12年福建卷第9题)若曲线 y=2x的图像上存在点(x，y)满足约束条件，则实数m的最大值为____________。

图9

由于曲线y=2x与可行域边界的交点为A(1，2)，而它实际上就是曲线y=2x与可行域的最右端的极限点，由此，过A(1，2)的直线x=1就是满足条件的最右端的直线，即极限直线;所以，实数m的最大值就是1。