卫星姿态对JASON-2卫星精密定轨影响分析
2013-01-14盛传贞甘卫军赵春梅陈为涛孙保琪梁诗明
盛传贞,甘卫军,赵春梅,陈为涛,孙保琪,梁诗明
(1.中国地震局地质研究所地震动力学国家重点实验室,北京100029;2.中国测绘科学研究院大地测量研究所,北京100830;3.中国科学院国家授时中心,陕西临潼710600)
0 引 言
2008年6月20日,美国宇航局(NASA)和欧洲气象卫星组织(EUMETSAT)成功将一颗海洋测高卫星JASON-2送入太空[1-4]。该卫星的主要任务是向地面传输全球海平面高度、洋流流速及方向、海洋内储存热量等海洋变化数据[2,4]。这些数据将有助于提高飓风预测准确度、为船舶提供可靠的海事气象预报和对全球气候变暖的规模及影响进行准确评估[4]。
为保证高精度的空间对地分辨、识别和定位能力,要求JASON-2卫星的空间对地指向,即卫星姿态具有较高的准确性和稳定性[2-4]。同时,高准确度和稳定性姿态也是为获得高精度的卫星轨道,为大地水准面和海洋动力学研究提供坚实保障的前提[3,4]。
卫星姿态描述的是卫星本体坐标系在参考系的指向,通过卫星姿态可将本体坐标系下的相位中心转换到卫星观测坐标系下,而后对观测量进行改正[5,6]。因此,姿态通过影响观测值的相位中心改正,从而影响定轨精度[6],关于观测量的卫星相位中心改正模型,许多文献都进行过讨论[3-7],但针对卫星姿态的稳定性对定轨精度的影响至今尚未述及。开展卫星姿态稳定性及对卫星精密定轨精度影响的研究具有重要的意义,因为卫星应用首先需要高稳定性、高可靠性的卫星姿态和高精度的卫星轨道[4,6-9],同时高精度的卫星轨道也亟需卫星姿态满足一定的稳定性,尤其是无姿态数据直接对卫星姿态模型进行精密定轨时[6,10-12]。此外,研究卫星姿态不稳定对轨道的影响也为后续海洋卫星姿轨控制提供相关的理论依据[8]。因此,笔者从卫星姿态对卫星精密定轨的影响出发,探讨了卫星姿态模型和卫星姿态变化对观测量的影响,并分析了卫星姿态的不稳定性对卫星精密定轨的影响,最后通过实测的JASON-2数据对姿态稳定性和轨道精度进行了评估。
1 姿态模型
姿态模型是对卫星实际运行姿态的近似和数学化描述,影响转换矩阵R2(Ψ)与轨道角(Ω)和β角(β')的关系[10]。
根据Ω和β'的角度关系,将JASON-2卫星姿态模型分成以下几种姿态调整模式。
1)固定姿态模式

2)正弦姿态模式
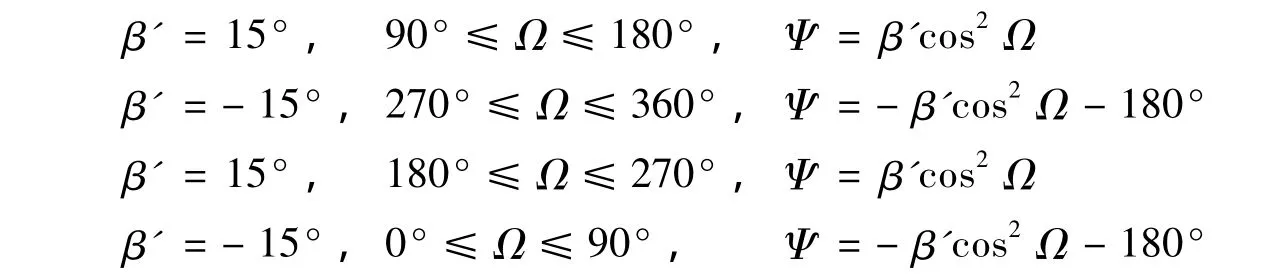
3)名义姿态模式

4)姿态翻转模式
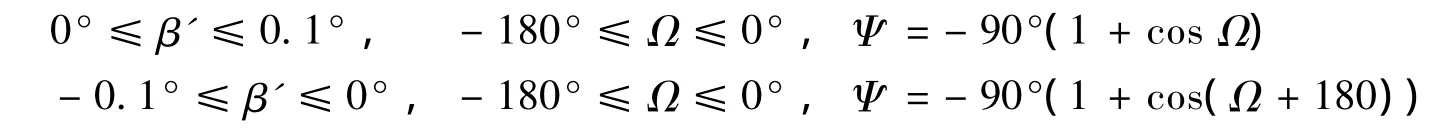
其中


其中Xsun,Ysun和Zsun是J2000坐标系下太阳位置坐标。Rsun为太阳到地心的距离,XP,YP和ZP为卫星在卫星位置坐标系(SPF:Satellite Position Frame)下的位置,X0,Y0,Z0为卫星在J2000下位置坐标,R0为转换矩阵(参考下文定义)。卫星位置坐标系定义参考文献[6,11-14]。
需要说明的是,在卫星精密轨道确定中,考虑到卫星姿态模型处理相对较复杂,通常进行简化处理,忽略姿态翻转模式。
2 姿态变化对观测量的影响
卫星姿态描述的是卫星本体坐标轴的空间指向。若已知卫星的姿态,基于该姿态可实现卫星本体系相位中心到观测系的转化,进而对观测值进行改正[5,6]。然而,由于卫星在轨时会受到多种力矩的综合影响,难以精确地模拟卫星的实际姿态[4,6,7,15],通常通过姿态模型对实际的姿态进行近似模拟。即卫星姿态模型为已知的理论模型,而卫星实际姿态是对该模型的逼近,两者之间并非完全一致,存在着差异,这些差异会影响到观测量相位中心改正精度。
假设卫星在J2000下,位置速度为(X0,Y0,Z0,X·0,Y·0,Z·0),仪器的相位中心在卫星固定坐标系(SBF:Satellite Body-Fixed Frame)和地心惯性系(J2000)下坐标分别为(XVc,YVc,ZVc)和(X0c,Y0c,Z0c),关于 SBF和J2000坐标系统的详细定义参考文献[16,17]。两者之间的转化关系为[6,18]
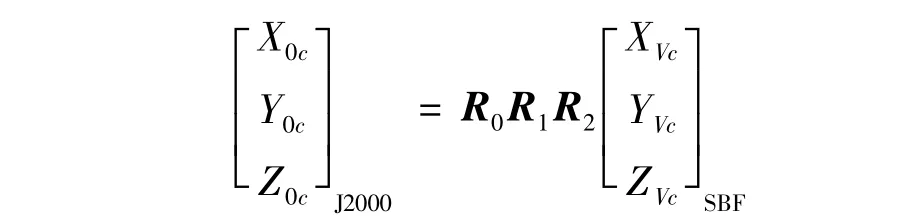
其中R0,R1和R2分别为转换矩阵,其定义为

其中 A1,A2,A3,Ry,Rx,Rxy和 α 的计算如下
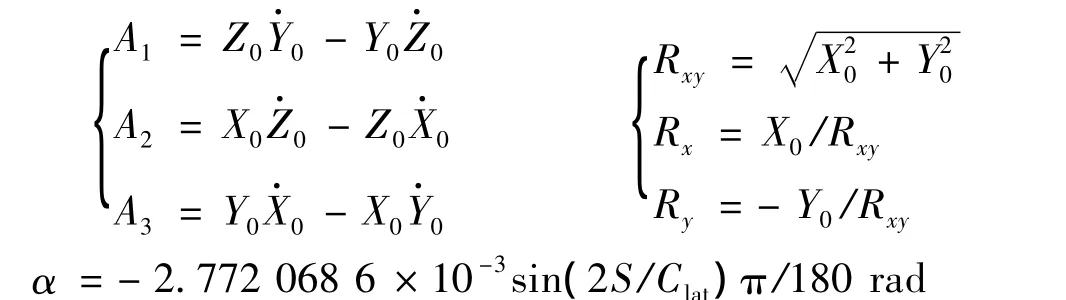
而Ψ主要由轨道角Ω和β角β'决定,而Ψ与Ω和β'的相互关系依赖于卫星的姿态模型。
定义Ratt=R0R1R2为基于姿态模型获得的卫星固定坐标系到J2000下的转换矩阵。若基于实测的姿态计算的转移矩阵为则因姿态的变化而引起的观测量改正为

其中 δx,δy,δz为观测坐标系下的相位中心改正量,RRot为 J2000坐标系与观测坐标系的转换矩阵[18,19]。
3 仿真实验
通常在无姿态调整状态下,卫星姿态模型被认为是可靠的姿态参考标准,该模型为理论模型,是基于数学表达式对实际姿态运行状况的近似描述。因此,在无姿态调整时通常可将其视定为参考标准,进行精密轨道确定。而实际观测的姿态可认为是对该姿态模型的最佳逼近,会随着卫星在轨所受力矩变化而变化,具有相对不稳定性。如果已知实测姿态矩阵R'att,通过与姿态模型获得的姿态矩阵Ratt进行比较,即可对姿态稳定性进行评估。
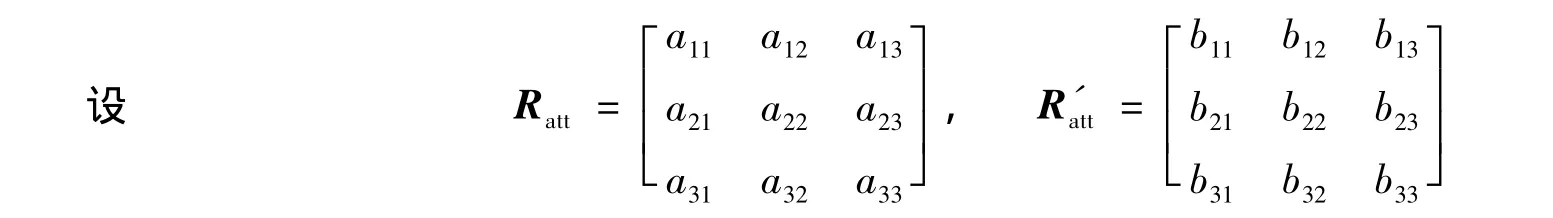
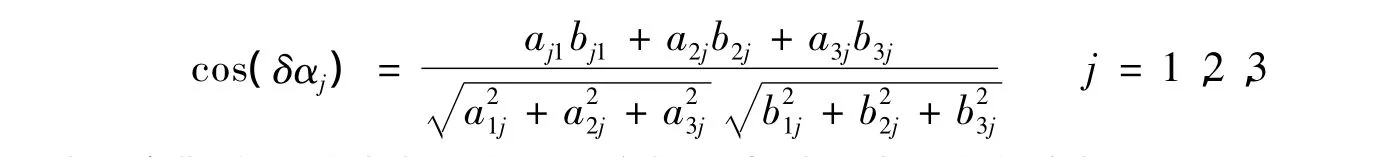
则基于δαj可统计其离散度,反映出姿态的稳定性,达到评估姿态稳定性的目的;反之,也可通过此方法分析姿态的不稳定性对轨道的影响:通过在各坐标轴向加入某一分布的角度抖动,即通过调整R'att使 δαj满足某一分布,通过调整的R'att对卫星进行定轨计算,并与基于Ratt计算的轨道进行比较,以研究姿态不稳定性对轨道的影响。文中基于2009年01月21日~01月25日的JASON-2 GPS双频观测数据进行了仿真实验,实验中令δαj满足N(0,n)分布,根据n的取值情况分别进行轨道计算并与Ratt计算的轨道进行比较。定轨中除姿态矩阵不同外,两者所采用定轨策略和数据均一致,具体定轨软件和定轨策略参考文献[20]。
通过统计基于模拟姿态和模型姿态计算的轨道差异,评估卫星姿态不稳定性对精密定轨的影响,采用每天的轨道位置差异Δ pl进行轨道的比较,其计算如下
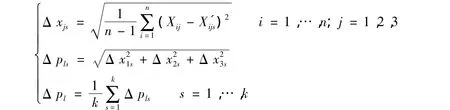
其中Xij为基于姿态模型矩阵计算的卫星在i历元、j方向上坐标,将该卫星位置作为标准轨道。为基于s次模拟姿态矩阵计算的卫星i历元、j方向上坐标,Δ pls为轨道位置差异RMS(Root Mean Square),Δ pl为Δ pls的均值,k和n分别为模拟次数和历元数,其中k选取为10。
基于每天的轨道位置差异Δ pl,求每天轨道差异RMS均值和标准差δp
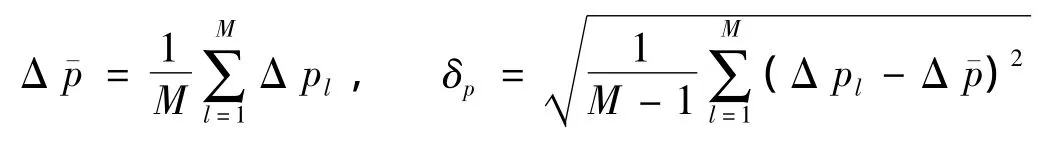
其统计结果如表1和图1所示。

表1 基于不同n值的每天轨道差异RMS均值和标准差统计表 mTab.1 Statistical chart of mean and standard deviation of RMS of position difference of each day based on different values of n

图1 基于不同n值的各天轨道差异RMS均值和标准差统计图Fig.1 Statistical values of mean and standard deviation of RMS of position difference of each day based on different values of n
通过表1和图1可看出,随着n的增大,姿态的不稳定性也增大,其卫星的轨道差异随之增大。当姿态的不稳定性维持在2°内时,轨道的差异并不明显;然而,当不稳定性继续增大时,轨道的差异呈现线性增长,且线性增长的斜率逐渐增大。因此,应保证姿态稳定性处于一定范围内。
此外,笔者通过设定δαj在一个方向满足N(0,5°),另外两个方向满足N(0,3°)分布,采用表1的统计方法统计轨道差异说明姿态在每个轴向的不稳定性对轨道影响是否相同,其结果如表2所示。

表2 各轴向姿态分布差异的各天轨道差异RMS均值和标准差统计表 mTab.2 Statistic values for mean and STD of RMS of position difference of each day based on different attitude variation in difference direction
通过表2和图2可看出,姿态的不稳定性在每个轴向的表现并不一致,在第1个方向明显要大于第2和第3个方向。考虑到相位中心在每个方向的值并不相同,以JASON-2为例,其相位中心在本体坐标系下为(1.428 5,-0.216 4,-0.472 1)[2,3],因此这种轴向的差异性更多源于相位中心在各个分量的差异。因此,在实际的卫星仪器安装中,尽量让其相位中心靠近于质心位置且保证相位中心较大方向的姿态稳定性。
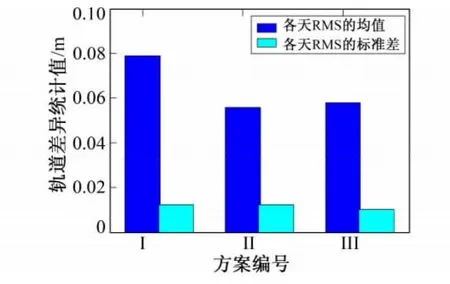
图2 各轴向姿态分布差异的各天轨道差异RMS均值和标准差统计图Fig.2 Statistic values for mean and STD of RMS of position difference of each day based on different attitude variation in difference direction
4 JASON-2姿态稳定性评估
上述提到,通过实际观测的姿态矩阵R'att和模型确定的姿态矩阵Ratt可计算δαj,然后基于δαj可以对卫星的姿态稳定性进行评估,进而通过轨道计算评价姿态稳定性对轨道的影响。因此,基于2009年01月21日~01月29日实测的GPS双频观测数据和姿态矩阵,对姿态的稳定性进行了评价,并对轨道的影响进行了评估。姿态的评估结果采用公式

其中M代表待评估的天数,δαijm为坐标轴j方向上第m天第i历元时刻的姿态角度偏差,n为每天历元数,j为各坐标轴方向,而轨道精度评估仍然采用表1的统计方法。通过计算,姿态稳定性在第1~第3个方向上分别为0.93°、1.030°和0.718°。轨道差异为0.036 m,与模拟结果的精度水平一致。
5 结 论
笔者分析了卫星姿态稳定性对卫星精密定轨精度的影响,并通过仿真数据进行了实验,通过实测数据对JASON-2卫星姿态稳定性及对轨道的影响进行了评估。得出以下结论。
1)当姿态的不稳定性增大时,其轨道的精度随之降低,当不稳定状态位于2°内时,其轨道差异性并不明显,然而当姿态的不稳定性继续增大时,其轨道精度随之迅速降低,且呈现线性趋势。
2)姿态不稳定性在每个轴向的差异对轨道的影响是不同的,这种轴向的差异性更多源于相位中心偏差在每个分量的差异性。
3)通过实测数据对JASON-2卫星进行姿态稳定性评估,表明其姿态的不稳定性在第1~第3个方向上,分别为0.93°、1.030°和0.718°,对轨道精度会产生3.6 cm的位置差异。
因此,对JASON-2类型的海洋卫星,卫星姿态不稳定性会对轨道的精度产生一定的影响。当卫星的姿态不稳定性维持在一定范围内时,对轨道的影响并不明显,当姿态的不稳定性继续增大时,其轨道精度随之迅速降低。姿态的不稳定对轨道的影响还体现在对各个分量上的差异性。因此,为了提高卫星的精密定轨的精度,应将卫星的姿态不稳定性维持在一定范围内,尤其是相位偏差较大的方向。此外,在卫星设备安装时,将仪器安装在靠近质心的位置,同样可以减小姿态不稳定性对轨道的影响,这些结论对我国目前及后续的海洋卫星计划,尤其是海洋二号卫星,具有重要的参考意义。
[1]STAVROS A MELACHROINOS,FRANK G LEMOINE,NIKITA P ZELENSKY,et al.Status of Precise Orbit Determination for Jason-2 Using GPS,SLR,DORIS Data at NASA/GSFC[J].Geophysical Research Abstracts,2011,13(9):2697.
[2]LEMOINE F G,ZELENSKY N P,CHINN D S,et al.Towards Development of a Consistent Orbit Series for TOPEX/Poseidon,Jason-1 and Jason-2 [J].Adv Space Res,2010,46(12):1513-1540.
[3]RIES J C.Orbit Error Budget for TOPEX/Poseidon and Jason-1 Precision Orbit Determination[J/OL].[2010-08-21].http://www.marine.csiro.au/conf/ostst/talks/WedTasA/06_Ries_POD.pdf.
[4]BECKLEY B D,ZELENSKY N P,HOLMES S A,et al.Assessment of the Jason-2 Extension to the TOPEX/Poseidon,Jason-1 Sea-Surface Height Time Series for Global Mean Sea Level Monitoring [J].Marine Geodesy,2010,33(S1):447-471.
[5]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,2005.ZHANG Ren-wei.Dynamic and Control of Satellite Orbit and Attitude[M].Beijing:Beihang University Press,2005.
[6]CHEINWAY HWANG,TZUPANG TSENG,LIN Ting-jun,et al.Quality Assessment of FORMOSAT-3/COSMIC and GRACE GPS Observables:Analysis of Multipath,Ionospheric Delay and Phase Residual in Orbit Determination [J].GPS Solution,2010,20(14):121-131.
[7]刘光炎,林幼权.星载SAR成像对卫星姿态控制精度的要求[J].中国电子科学院学报,2007,2(2):109-114.LIU Guang-yan,LIN You-quan.The Demand of Satellite Attitude Control in Space-Borne SAR Imaging [J].Journal of CAEIT,2007,2(2):109-114.
[8]林明森.海洋二号卫星用户需求分析[J].卫星应用,2010,11(2):7-14.LIN Ming-sen.The Demand Analysis of HY-2 Ocean Altimeter Satellite for User [J].Satellite Application,2010,11(2):7-14.
[9]LE BAIL K,LEMOINE F G,CHINN D S.GSFC DORIS Contribution to ITRF2008[J].Adv Space Res,2010,45(12):1481-1499.
[10]JAGGI A,BOCK H,FLOBERGHAGEN R.GOCE Orbit Predictions for SLR Tracking [J].GPS Solut,2011,15(2):129-137.
[11]李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995.LI Ji-sheng.Precision Orbit Determination of Artificial Satellite[M].Beijing:People's Liberation Army Press,1995.
[12]赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉:武汉测绘信息科学大学测绘学院,2004.ZHAO Qi-le.Research on Precise Orbit Determination Theory and Software of Both GPS Navigation Constellation and LEO Satellite GPS[D].Wuhan:College of Geomatics,Geomatics and Information Science of Wuhan University,2004.
[13]JAGGI A,PRANGE L,HUGENTOBLER U.Impact of Covariance Information of Kinematic Positions on Orbit Reconstruction and Gravity Field Recovery[J].Adv Space Res,2011,47(10):1472-1479.
[14]PENG Dong-ju,WU Bin.Zero-Difference and Single-Difference Precise Orbit Determination for LEO Using GPS[J].Chinese Science Bulletin,2007,52(6):715-719.
[15]JAGGI A,HUGENTOBLER U,BOCK H,et al.Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data[J].Adv Space Res,2007,39(10):1612-1619.
[16]TAPLEY B D,SCHUTZ B E,BORN G H.Statistical Orbit Determination[M].[S.l.]:Elsevier Academic Press,2004.
[17]HAINES B,BERTIGER W,DESAI S,et al.Initial Orbit Determination Results for Jason-1:Towards a 1-cm Orbit[J].Journal of Navigation,2003,50(3):171-179.
[18]BEUTLER G.Methods of Celestial Mechanics[M].Berlin Heidelberg:Springer,2010.
[19]CERRI L.Preliminary Strategy for Jason-2 POD,in:Presentation[C]∥DORIS Analysis Working Group Meeting(AWG)of the International DORIS Service.Paris:IDS Publish,2008:1520-1532.
[20]盛传贞,甘卫军,赵春梅,等.JASON-2卫星精密轨道确定:GPS、SLR和DORIS分析[J].中国科学:物理学,力学,天文学,2013,43(2):219-224.SHENG Chuan-zhen,GAN Wei-jun,ZHAO Chun-mei,et al.Precise Orbit Determination of JASON-2 Satellite:Analysis of GPS,SLR and DORIS[J].Scientia Sinica Physica,Mechanica& Astronomica,2013,43(2):219-224.
