基于BP神经网络的太白山生态旅游量预测研究
2013-01-13李崇实樊金拴
李崇实,樊金拴
(西北农林科技大学,陕西 杨凌712100)
生态旅游是二战以后旅游业中增长最快的部分,已成为当今世界旅游业发展最快的热点,世界各地区和国家都在积极发展生态旅游,中国生态旅游发展时间较短,但近几年取得了巨大的发展。然而,随着生态旅游业的蓬勃发展,与之形成反差的是旅游管理质量和水平的落后,其中一个关键性衡量指标就是旅游预测与发达国家相比还处于学习阶段。所以生态旅游的需求预测应该是且必须是今后研究的一个重要课题。如何建立科学的可操作性的生态旅游预测模型,准确地把握生态旅游需求的发展趋势,以制定适合生态旅游调控政策,对生态旅游的持续健康发展具有重要意义。
由于旅游具有很强的易波动性,故而很难从宏观上把握其发展趋势。因此在研究旅游需求趋势时必不可少地需要使用数学方法与运用模型。国外专家学者对旅游需求的预测主要以定量分析为主,分析方法包括回归模型法、时间序列法、计量经济学模型、德尔菲法等等,这些传统的技术分析方法取得了较大的成就。但是当系统具有较强的非线性时,这些方法的适应性却是有限的,在实际的预测环境中常常失去效用,因此用这些传统的预测方法解决这类问题十分困难。为此,本文采用BP神经网络模型,通过改进算法,提出收敛性较快、网络泛化能力强的神经网络模型,并对太白山保护区未来10年来的旅游数据进行了预测分析,这对于全面深刻了解太白山保护区生态旅游需求,充分挖掘潜在客源市场,深化生态旅游消费市场的开拓有所裨益,同时也可以为太白山生态旅游的发展提供依据。
1 神经网络的概念及原理
人工神经网络[1,2](Artificial Neural Network)常常简称为神经网络(ANN),是以计算机网络系统模拟生物神经网络的智能计算系统,是对人脑或自然神经网络的若干基本特性的抽象和模拟,是智能控制领域的一个新的分支,为解决复杂的非线性、不确定性、不确知系统的控制问题开辟了一条新的途径。它因为具有函数近似、数据聚集、模式分类、优化计算、概率密度函数估计等功能,在工程领域得到较多的应有。而目前,人工神经网络可以用来解决模式信息处理和模式识别、控制优化、信息的智能优化处理、复杂控制、信息控制、故障诊断这几类问题。
反向传播网络[3](Back-Propagation Network,简称BP网络)是1986年由Rumelhart和McCelland为首的科学家小组提出,将W-H学习规则一般化,对非线性可微分函数进行权值训练的多层网络。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)(图1)。

图1 BP神经网络结构示意图
如图1所示,一个BP神经网络由输入层、输出层和至少一个隐层组成,各层包含一个或者多个神经元,相邻两层神经元之间通过可调权值相连接,且各神经元之间没有反馈。BP算法由信号的前向计算(正向传播)和误差信号的反向传播2个过程构成。正向传播时,传播方向为输入层→隐层→输出层,每层神经元的状态只影响下一层神经元。若在输出层得不到期望的输出,则转向误差信号的反向传播流程。误差的反传是将输出误差以某种形式通过隐层向输入层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号并将其作为修正各单元权值的依据。通过这2个过程的交替进行,在权向量空间执行误差函数梯度下降策略,动态迭代搜索一组权向量,使网络误差函数达到最小值,从而完成信息提取和记忆过程。
2 太白山生态旅游模型的建立
2.1 旅游指标
2.1.1 旅游者人数 旅游者人数是指旅游目的地国家或地区在一定时期内所接待的旅游者总人数,主要用来衡量旅游者对旅游产品的需求总量状况。
2.1.2 旅游者停留天数指标 旅游者停留天数分为旅游者停留总天数和旅游者人均停留天数。旅游者停留总天数是指一定时期内旅游者人次与人均过夜数的乘积;旅游者人均停留天数是指一定时期内旅游者停留天数与旅游者人次的除数。
2.1.3 旅游者消费指标 旅游者消费指标分为旅游者消费总额和旅游者人均消费额。旅游者消费总额是指一定时期内旅游者在旅游目的地国家或地区的全部货币支出,如旅游者在旅游过程中支出的餐饮费、住宿费、交通费等;旅游者人均消费额是指一定时期内旅游者消费总额与旅游者人次之比。
衡量一个地区旅游需求状况,可以从该地区的旅游需求总量和旅游消费总额2个指标考虑。因此,本文选择反映旅游需求的基本指标是以上山游客人数作为预测对象,其余预测方法同理。
2.2 BP神经网络预测模型的建立
2.2.1 传递函数的选择 BP网络通常有一个或多个隐含层,该层中的神经元均采用sigmoid型传递函数,输出层的神经元则采用线性传递函数,整个网络的输出可以取任意值。通过训练BP网络时发现,传递函数使用tansig函数时要比logsig函数的误差小。于是在以后的训练中隐层传递函数改用tansig函数,输出层传递函数仍选用purelin函数。
2.2.2 结构模型
(1)网络的层数。已经证明:三层BP网络可以实现多维单位立方体Rm到Rn的映射,即能够逼近任何有理函数。这实际上给了一个设计BP网络的基本原则。增加层数可以更进一步降低误差,提高精度,但同时也使网络复杂化,从而增加网络权值的训练时间。所以一般情况下,应优先考虑增加隐含层的神经元个数。本研究采用一个隐含层的3层BP模型。
(2)各层的神经元数。神经网络的输入层和输出层的节点数是由求解问题本身以及数据的表示方式综合确定的。根据旅游需求的已有数据,确定输入层的神经元个数为2,输出层的神经元个数为1。
网络训练精度的提高,可以通过采用一个隐含层而增加神经元数的方法来获得,这在结构的实现上要比增加更多的隐含层简单得多。但是隐层节点数对网络的泛化能力有很大的影响。节点数太多,倾向于记住所有的训练数据,包括噪声的影响,反而降低了泛化能力;节点数太少,不能拟和样本数据,没有较好的泛化能力。所以我们要选择合适的节点数。通过多次试验,确定隐含层结点个数为8。
(3)数据的获取。本文数据来自《太白山自然保护区生物多样性研究与管理》《太白山自然保护区(2011—2020)十年总体规划》及太白山保护区各保护站生态旅游数据,见表1。
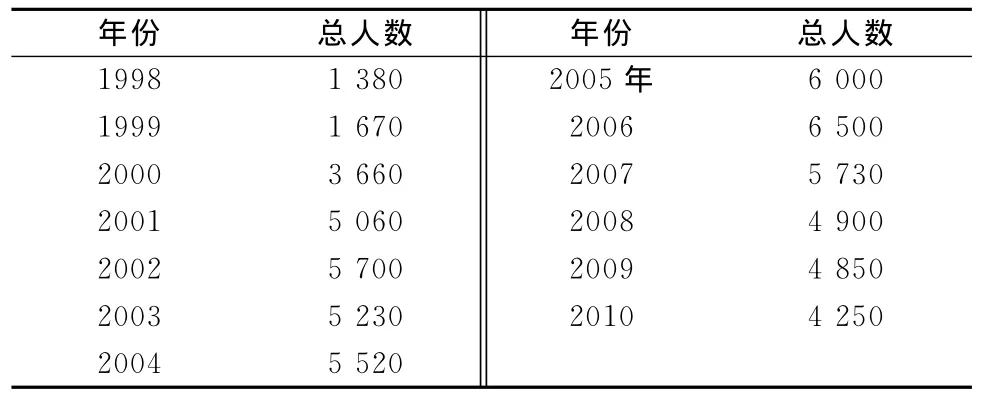
表1 太白山自然保护区1998—2010年生态旅游人数
为了提高训练速度和灵敏度以及有效地避开激活函数的饱和区域,一般要求输入数值在0—1之间。如不对数据进行预处理,预测结果误差较大,训练时间过长。本课题将对数据乘以10-4做归一化处理,所得结果如下:
p=[0.138 0 0.167 0 0.366 0 0.506 0 0.570 0 0.523 0 0.552 0 0.600 0 0.650 0 0.573 0;0.167 0 0.366 0 0.506 0 0.570 0 0.523 0 0.552 0 0.600 0 0.650 0 0.573 0 0.490 0]
(4)网络设计。在进行建模时,根据采样方法,将数据分为11组,构成训练和测试样本集,其中前10组为网络训练样本集,后一组为网络测试样本集。用1998—1999年、1999—2000年、2000—2001年……2007—2008年的数据作为神经网络的输入,用2000年、2001年、2002年……2009年的数据作为理想输出,组成样本集对网络进行训练,直到网络设置的误差预期为止,然后保存网络并用网络预测随后几年的旅游人数。
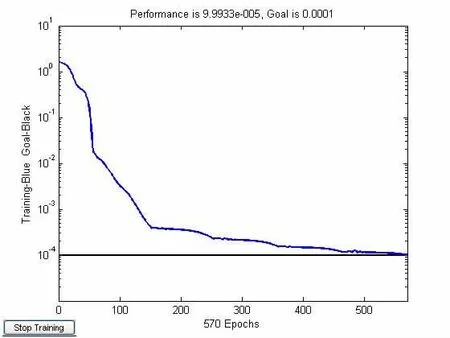
图2 训练误差曲线
即输入层节点2个,输出层节点为1个。根据实验,确定隐含层节点为8个,因此,BP网络结构为:2-8-1。用MATLAB神经网络工具箱中的函数TRAINGDM进行训练,当训练到570次的时候,误差达到要求,如图2所示。
3 预测结果分析
3.1 网络仿真
为了检验网络对未知样本的预测效果,也就是网络的泛化能力,把2008—2009年的数据输入训练好的网络中得到预测值,见表2。

表2 2010年太白山自然保护区生态旅游人数实际值与预测值的比较
由对照表中的实际值和预测值可以看出,神经网络给出的预测结果很接近实际值,绝对误差4.45%,误差较小,验证了该模型的可行性。
3.2 网络预测
利用已建立好的神经网络模型预测未来几年太白山保护区生态旅游发展趋势,并将结果反归一化,如表3。
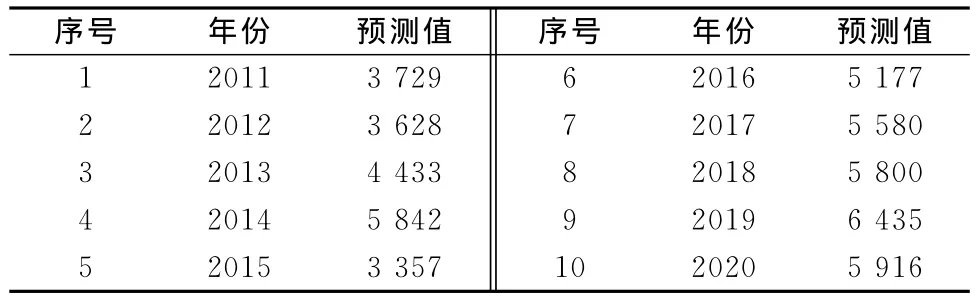
表3 太白山自然保护区未来10年旅游发展趋势
4 结论
4.1 以太白山自然保护区生态旅游建立预测模型得出未来10年生态旅游的发展趋势,为日后的管理决策提供了依据。
4.2 采用BP神经网络建立的预测模型,要对输入的原始数据做预处理,这样能够加快收敛速度,缩小误差范围,从而得到更好的预测效果。
[1]徐丽娜.神经网络控制[M].哈尔滨:哈尔滨工业大学出版社,2003
[2]朱大奇.人工神经网络研究现状及其展望[J].江南大学学报:自然科学版,2004(1):103-110
[3]周政.BP神经网络的发展现状综述[J].山西电子技术,2008(2):50-54
