基于耦合分析法的涡轮增压器浮环轴承数值仿真

(湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙，410082)

涡轮增压器水冷轴承体是增压器结构中的重要环节，其各部分的温度分布不均匀且存在较大温差，承受着很大的热应力[1−2]。它的冷却性能直接影响着涡轮增压器的可靠性，在很大程度上决定了涡轮增压器的寿命[3−4]。在涡轮增压器的使用中，最早采用滚动轴承，随后发展至滑动轴承和全浮动轴承[5−6]。浮环轴承是一种被浮环隔开的双膜润滑全浮动轴承，具有尺寸小、结构简单、磨损小、效率高等优点。由于浮环以一定转速旋转，相应地减小了与轴颈和轴承座孔之间的相对速度，从而可减小剪切引起的功率损失[7−8]。浮环轴承的特点是它的功耗低，对于很好的浮环轴承，可在相同的承载能力下，比普通轴承的功耗降低 20%～30%[9−10]。浮环轴承在复合载荷作用下容易产生裂纹，进而断裂，使涡轮增压器发生故障造成事故。为此，本文作者采用多物理场的耦合分析法对涡轮增压器的浮环轴承进行研究，以便为涡轮增压器的优化设计提供理论分析依据。

1 涡轮增压器耦合分析基本原理

涡轮增压器水冷轴承体传热的数学模型包括冷却水和机油的流动与传热模型、轴承体固体导热模型和冷却介质与轴承体复杂结合面的耦合传热模型。

1.1 涡轮增压器水冷轴承体三维瞬态热传导模型

对于三维直角坐标问题，描述涡轮增压器水冷轴承体瞬态热传导的微分方程为[11]

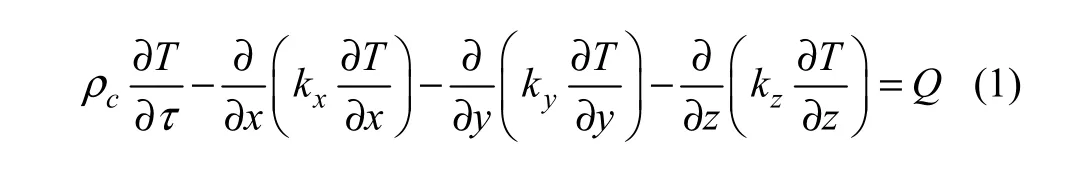
式中：ρ为密度；c为比热容；τ为时间；kx，ky和kz分别为物体沿x，y和z3个坐标轴方向的热传导系数；Q为物体的内热源密度，这里指润滑摩擦过程中轴承体−浮环轴承之间的摩擦热分配给轴承体和浮环轴承的部分。

1.2 涡轮增压器浮环轴承的润滑模型

浮环的存在使内外油膜的压力分布相互影响，当某一层油膜的状态发生改变时，浮环的瞬时位移与速度也会发生改变，从而影响另一层油膜的状态。表达内外层油膜压力分布的雷诺方程为[12−13]：

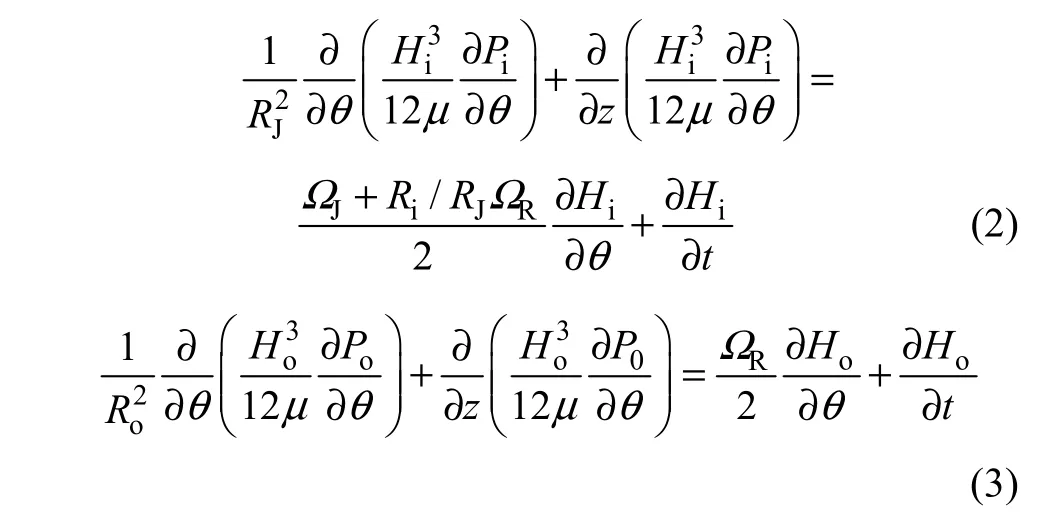
式中：RJ，Ri和Ro分别为轴颈、浮环内圈与浮环外圈的半径；μ为润滑油黏度；ΩJ和ΩR分别为轴颈与浮环的角速度；θ为从y轴起始的顺时针角度。

1.3 涡轮增压器耦合边界的共轭传热

流固耦合传热只在边界上存在热量交换，其边界上的温度、换热系数都应看成是计算结果的一部分，而不是已知条件，关键在于解决流体与固体壁面之间的热量传递问题[14−15]。

在涡轮增压器流固耦合传热边界上，有

式中：qw为壁面释放的热量；qf为流体吸收的热量。

当黏性流体在贴近壁面附近流动且流速很小时，其相对运动可忽略不计。在涡轮增压器水冷轴承体壁面流体层处，由傅里叶热定律，有

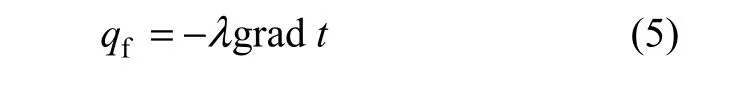
式中：λ为导热系数；gradt为贴近壁面法线方向上流体温度变化率。对流传热的牛顿冷却公式为

阿Q平生最大的遗憾，不是没王胡身上虱子多、没打过小D、没和吴妈困觉，也不是挨过假洋鬼子一哭丧棒，而是在判决书上那个圆圈没画圆。迅翁说得详细：“阿Q伏下去，使尽了平生的力气画圆圈。他生怕被人笑话，立志要画得圆，但这可恶的笔不但很沉重，并且不听话，刚刚一抖一抖的几乎要合缝，却又向外一耸，画成瓜子模样了。”

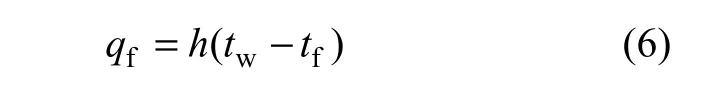
由式(5)和(6)可以得到对流传热表面换热系数与流体温度场的关系式：

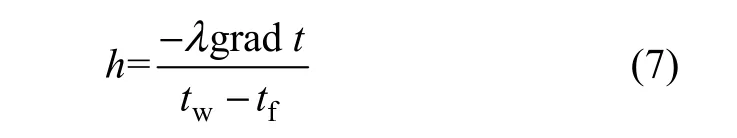
式中：tw为壁面的温度；tf为流体的温度。

2 涡轮增压器轴承体数值仿真模型

2.1 涡轮增压器轴承体耦合分析计算流程

为减少边界条件和更好地反映实际工作情况，采用数值法进行研究。若只运用单一综合性有限元软件对正常工况下涡轮增压器水冷轴承体冷却性能进行数值模拟仿真计算，很难在减少计算量的同时保证较高计算精度[14−15]，为此，对轴承体固体和冷却水腔流体分别建模，采用有限元软件和计算流体力学软件分别仿真计算，再通过编译文件实现数据相互之间的传递，较好地体现了有限元软件和计算流体力学软件在固体、流体领域模拟仿真的优势。结合 Fire和 Abaqus软件特点，按图1所示流程实现涡轮增压器水冷轴承体冷却性能数值仿真模型的流固耦合计算。将Fire软件计算所得的流体边界温度T与对流传热系数h映射到有限元网格上，利用Msc patran耦合面网格和轴承体内表面的温度自由度，在 Abaqus中将其转换成热交换边界条件。再将 Abaqus计算所得的固体壁面温度映射到面网格节点上作为流体计算的壁面条件，在Fire软件中进行计算。按此步骤重复迭代耦合，直至温度收敛为止。

2.2 涡轮增压器轴承体仿真模型

在实际工作中，涡轮增压器轴承体同时传递热量给机油、冷却水、涡轮轴、涡轮箱、压气机，传热情况十分复杂。在进行数值仿真时，对轴承体外表面倒角和细小结构进行简化，忽略对于轴承体传热影响很小的部件。

图1 涡轮增压器浮环轴承耦合分析计算流程图Fig.1 Flow chart of fluid−solid coupling calculation for floating ring bearing of turbocharger

在三维软件中，按照轴承体实际尺寸建立几何模型并导入Hypermesh中，划分机油腔、冷却水腔面网格和涡轮增压器轴承体三维网格。为了保证内部细小尺寸结构逼近程度，采用全四面体划分轴承体网格。同时，为了更精确模拟壁面附近的流动和传热特性，将机油腔、冷却水腔表面网格导入到Fire软件中，利用其前处理模块fame对进、出口网格和表面网格进行局部加密以及对边界层网格应进行细化，采用四面体、六面体混合划分网格的方法划分流体网格，如图2所示。

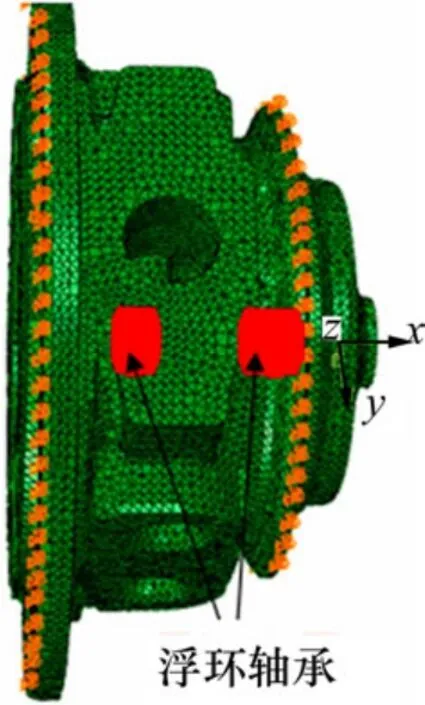
图2 涡轮增压器轴承体有限元模型Fig.2 Finite element model of turbocharger bearing

3 涡轮增压器浮环轴承数值仿真

本文研究的是正常工况下涡轮增压器水冷轴承体稳定运行时的冷却情况，其传热边界条件通过相应试验测取。当涡轮增压器轴转速为60 000 r/min时，控制涡轮进气温度为950 ℃，进口废气流量为0.12 kg/s，冷却水进口温度为75 ℃，机油进口温度为100 ℃。假设涡轮增压器水冷轴承体内冷却水和机油的流动为三维不可压缩流动，入口采用压力边界，冷却水进水压力为2.5 MPa，机油进口压力为0.5 MPa。通过对涡轮增压器轴承体有限元模型进行数值仿真，得到轴承体浮环轴承的温度与应力分布。

3.1 浮环轴承座温度场分布

图3 涡轮增压器轴承体轴向方向温度分布Fig.3 Temperature distribution of turbocharger bearing in axial direction

图4所示为浮环轴承温度分布情况，温度最高区域位于浮环轴承部位。这是因为虽然热量主要是从轴承体涡轮端传向压气机端，但涡轮轴在高速运转中产生的部分热量传递至轴承体引起局部温度过高。

结合图3和图4可以看出：从涡轮增压器水冷轴承体的涡轮端至压气机端冷却水和机油起到了很好的冷却作用，显著减少了热量的传递，特别是在水腔和油腔附近，轴承体温度下降极明显。

图4 涡轮增压器轴承体中浮环轴承横截面温度分布Fig.4 Cross section temperature distribution of floating ring bearing in turbocharger bearing

3.2 浮环轴承应力场分布

图5和图6所示为浮环轴承应力场分布。由图5和图6可见：在轴承座的全浮环轴承部位，等效应力远比其他部分的大，轴承座有向下变形和中间向四周变形的趋势。这是由于轴承座被固定，但是轴在高速旋转中，带动润滑油旋转，给轴承座浮环轴承座部位施加压力。

当x=−10 mm时，作yOz截面，截面经过轴承体浮环轴承座的涡轮端，它的等效应力等值线分布见图5。由图5可以看出：等效应力从5.38 MPa减少至2.39 MPa，沿半径方向逐渐减少；而在轴承体靠近厚壁面一侧(图中左侧)，等效应力远比相同半径长度相反一侧的小。

图5 浮环轴承在x=−10 mm时，yOz 剖面应力分布Fig.5 Stress field distribution of yOz profile at x=−10 mm along floating ring bearing

图6 浮环轴承在x=−30 mm时，yOz 截面应力分布Fig.6 Stress field distribution of yOz profile at x=−30 mm along floating ring bearing

当x=−30 mm时，作yOz截面，截面经过轴承体全浮环轴承座的压气机端，它的等效应力等值线分布图如图6所示。从图6可见：其分布趋势与轴承座浮环轴承座部位的涡轮端基本相同，但在油腔最底部，应力局部过大。

图7和图8所示分别为xOz和xOy截面轴承座浮环轴承部位等效应力等值线分布。从图7和图8可以看出：在轴承座的浮环轴承部位，等效应力从中间部位向两侧减小，从内侧向外侧减小。

图7 浮环轴承在xOz 平面应力分布Fig.7 Stress field distribution of floating ring bearing at xOz plane

图8 浮环轴承座在xOy平面应力分布Fig.8 Stress field distribution of floating ring bearing at xOy plane

4 试验验证

4.1 涡轮增压器轴承体温度测点布置

在对涡轮增压器水冷轴承体的温度分布进行数值仿真时，传热边界条件的确定直接关系着仿真结果的精确程度。在正常工况下，尾气热量通过涡轮箱传递给轴承体，一部分被冷却介质带走，另一部分传导至压气机；同时，轴高速旋转所产生的一部分热量通过机油传递至轴承体。

为验证模拟仿真结果的准确性，需要在轴承体不同位置选择测量点，轴承体测温点分布如图9所示。

图9 轴承体测温点分布Fig.9 Distribution of measuring points on turbocharger bearing

4.2 涡轮增压器轴承体试验结果分析

在涡轮增压器稳态运行工况下进行试验，控制涡轮增压器转速为60 000 r/min，待增压器稳定运行20 min后测取边界条件和验证条件。

表1所示为6个测温点温度的仿真计算结果与实验结果的对比情况。从表1可见：各测点仿真计算结果与实测结果相对误差不超过3.0%。这说明基于耦合分析法的涡轮增压器轴承体浮环轴承模型仿真结果较好，验证了本文所设计的耦合分析计算方法的可行性。

表1 测点温度计算结果与实测结果的比较Table 1 Comparison between test and simulation temperature of measured points

5 结论

(1) 基于耦合分析法建立了涡轮增压器轴承体浮环轴承仿真模型，设计了一种涡轮增压器温度场的计算方法。该方法为分析涡轮增压器轴承体浮环轴承各参数与热传导的关系、揭示温度场分布规律提供了一种有效的数值仿真方法，为浮环轴承冷却系统的优化提供了依据。

(2) 浮环轴承应力主要集中在浮环轴承座的内壁部位，应力在内壁面达到最高值，从内向外降低。在轴承体的浮环轴承座部位，有向两端扭曲的趋势，且在中间某处，应力达到最大值。

(3) 模型仿真计算结果与试验结果较接近，符合涡轮增压器轴承体正常工作时温度分布，证明了该耦合仿真分析方法的可行性。

[1] 周虹伟.涡轮增压器主要部件结构特性及改进研究[J].中国铁道科学, 2004, 25(2): 72−77.ZHOU Hongwei.Structure characteristics and improvement of main components of turbo-supercharger[J].China Railway Science, 2004, 25(2): 72−77.

[2] 胡友安, 李晓东.涡轮增压器蜗壳热裂纹的试验研究[J].河海大学学报, 2008, 36(6): 846−849.HU Youan, LI Xiaodong.Experimental study on heat cracks of turbine housing on turbochargers[J].Journal of Hehai University,2008, 36(6): 846−849.

[3] 张俊红, 李志刚, 王铁宁.车用涡轮增压技术的发展回顾、现状及展望[J].小型内燃机与摩托车, 2007, 36(1): 66−69.ZHANG Junhong, LI Zhigang, WANG Tiening.Retrospect,status and expectation for turbocharger technology of vehicle[J].Small Internal Combustion Engine and Motorcycle, 2007, 36(1):66−69.

[4] Gluck M, Breuer M, Durst F, et al.Computation of wind-induced vibrations of flexible shells and membranous structures[J].Journal of Fluids and Structures, 2003, 17(1):739−765.

[5] 刘海亮, 马永青, 韩志引.汽车涡轮增压发动机工作原理及其优势研究[J].价值工程, 2011, 30(8): 57−58.LIU Hailiang, MA Yongqing, HAN Zhiyin.Research on the working principle of car turbocharged engine and its advantages[J].Value Engineering, 2011, 30(8): 57−58.

[6] ZHANG Jizhong, SUN Harold.Fault diagnosis and failure prediction by thrust load analysis for a turbocharger thrust bearing[C]//Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air.Glasgow, UK , 2010: 1−8.

[7] Kostandin G J I K A, Gerald D La R U E.Axial load control on high-speed turbochargers test and prediction[C]//Proceedings of ASME Turbo Expo 2008: Power for Land, Sea and Air.Berlin,Germany, 2008: 1−8.

[8] 胡友安, 李晓东, 陈图钧.涡壳温度场和热应力的有限元分析[J].机械强度, 2007, 29(1): 130−134.HU Youan, LI Xiaodong, CHEN Tujun.Analysis on temperature field and thermal stress of turbocharger housing by finite element method[J].Journal of Mechanical Strength, 2007, 29(1):130−134.

[9] 傅松, 胡玉平, 李新才, 等.柴油机缸盖水腔流动与沸腾传热的流固耦合数值模拟[J].农业机械学报, 2010, 41(4): 26−30.FU Song, HU Yuping, LI Xincai, et al.Fluid-solid coupling numerical simulation on flow and boiling heat transfer of cooling water-jacket in cylinder head of diesel engine[J].Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(4):26−30.

[10] 周龙, 白敏丽, 吕继组, 等.用耦合分析法研究内燃机活塞环−气缸套传热润滑摩擦问题[J].内燃机学报, 2008, 26(1):69−75.ZHOU Long, Bai Minli, LÜ Jizu, et al.Study of heat transfer,lubrication and friction of piston ring-liner in internal combustion engines using the coupled methods[J].Transactions of CSICE, 2008, 26(1): 69−75.

[11] 康召辉, 任兴民, 黄金平, 等.浮环轴承系统中浮动环作用机理研究[J].振动工程学报, 2009, 22(5): 533−537.KANG Zhaohui, REN Xingmin, HUANG Jinping, et al.Research of mechanism of a floating ring in the floating ring bearing system[J].Journal of Vibration Engineering, 2009, 22(5):533−537.

[12] SUN Zhigang, TAN Chunqing, ZHANG Dongyang.Flow field structures of the impeller backside cavity and its influences on the centrifugal compressor[C]//Proceedings of ASME Turbo Expo 2009: Power for Land, Sea and Air.Orlando, Florida, 2009:1−12.

[13] Szwedowicz J, Schafer O, Filsinger D.Approach to unidirectional coupled CFD-FEM analysis of axial turbocharger turbine blades[J].Journal of Turbomachinery, 2002, 123(1):125−131.

[14] Kenyon J A, Griffin J H, Feiner D M.Maximum bladed disk forced response from distortion of a structural mode[J].Journal of Turbomachinery, 2003, 125(2): 352−363.

[15] 杨金福, 陈策, 袁平, 等.浮环轴承非线性耦合动力润滑特性[J].航空动力学报, 2009, 24(2): 365−370.YANG Jinfu, CHEN Ce, YUAN Ping, et al.Research on nonlinear fluid-solid interaction dynamic lubrication in floating ring bearings[J].Journal of Aerospace Power, 2009, 24(2):365−370.