用波动方程讨论波的干涉问题

王兴堂

(江苏省沛县中学 江苏 徐州 221600)

波的干涉是“机械波”一章的重点和难点，同时也是高考的热点．对于波的干涉，由于教材运用静态的波形图加以分析，造成学生对动态的干涉问题理解不准、不深，往往只记住峰峰、谷谷点是加强点，峰谷相遇为减弱点等一些简单结论；至于波的干涉条件、加强、减弱的真正含义、加强和减弱的根本条件以及一般点的振动情况等问题理解不够．

本文尝试用波动方程及相关数学知识对波的干涉进行定量的研究，以期对大家的学习带来一定的帮助．

设某一波源的振动方程

y=Acos(ωt+ψ)

y=Acos[ω(t-Δt)+ψ]=

介质中不同位置的质点的x取值不同，该方程能够描述传播介质中所有质点的振动位移随时间变化的规律，也称为波动方程．

为了便于分析，假设两个波源振动完全相同，且初相为零，两波源的振动方程均为y=Acosωt，若在两波源传播的重叠区域任选一点P，P到两波源的距离分别为x1,x2,则两列波在P点引起振动的振动方程分别为

根据波的叠加原理，质点P的振动位移

从表达式形式看，前一项是不变量表示振幅，后一项表明位移按余弦规律变化,说明质点P仍做简谐振振动．下面利用该式进一步分析如下.

(1)质点P的振幅为

当x1-x2=nλ，n为整数时，振幅最大为2A;

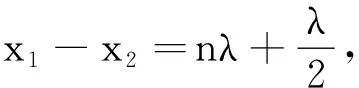
我们把振幅最大的点称为加强点，振幅最小的点称为减弱点．由此可知，决定质点振幅大小的是质点到两波源的距离差．另外，加强点和减弱点构成加强、减弱线，每条线上的点到两波源的距离差相同，故加强线、减弱线也就是数学上的双曲线．

需要说明的是:若两波源的振幅不同，则加强点振幅为A1+A2，减弱点振幅为|A1-A2|；若两波源振动完全相反，上述加强和减弱的条件刚好相反，比如x1-x2=nλ时，质点将不是加强点而是减弱点．

(3)对于介质中一般质点即非加强和减弱点，其振幅也是一定的，但其值介于最大振幅和最小振幅之间，而且从振动加强点到相邻的减弱点，质点振动振幅将不断减小．

(4)为什么只有频率相同的相干波源才能发生波的干涉呢？对此，我们也可以运用数学知识加以证明，设有两振幅相同，但频率不同的波源，其波动方程为

y1=Acosω1ty2=Acosω2t

设P点到两波源的距离为x1,x2，则两列波引起的位移分别为

P点位移y=y1+y2，化简后可得

表达式中两项都随时间按余弦函数变化，可理解为P点仍在振动，但其振幅也随着时间的变化而变化，从而不能形成固定的加强和减弱区，不能形成稳定的干涉图样，这种情况，我们称之为波的叠加，但不能称之为干涉，所以，发生干涉的条件应是频率相同、相位差恒定的同种波源．

综上所述，运用波动方程和相关数学知识开展教学，可以帮助学生对波的干涉中几个常见问题的理解更加准确和深刻．