坑中坑开挖影响下的基坑变形特性有限元分析
2013-01-11熊中华
熊中华
(河海大学 岩土工程研究所, 江苏 南京 210098)
随着我国基础建设的日益发展,高层建筑、地下商场、交通枢纽等工程逐渐增多,城市地下空间得到不断开发,基坑工程的数量也因此迅速增大。为了满足建筑物施工与使用过程中的各种需求,需要在原有基坑内部进行二次开挖,以得到能容纳地下室、电梯井、承台等结构的内部小坑,称为坑中坑或内坑。坑中坑式基坑不同于常规基坑,如图1所示,目前学术界对坑中坑式基坑的研究甚少,成果不多。龚晓南院士[1]曾结合上海基坑工程事故较早提出对坑中坑基坑工程进行研究;吴铭炳[2]在充分考虑内坑、外坑相互影响的情况下,对软土地基坑中坑支护设计计算深度的取值进行了探讨;徐意智[3]针对坑中坑工程设计中选取大基坑计算深度时所面临难题,提出了等效计算深度的概念并验证了其可行性。与常规基坑相比,坑中坑式基坑内坑的开挖打破基坑内部应力平衡,应力重新分布并形成二次应力场,严重影响基坑的整体稳定性[4]。但由于通常情况下内坑开挖范围较小,容易为工程设计人员所忽略而按照常规基坑进行设计,造成基坑工程事故[5,6]。文献[6]展示了一个坑中坑工程事故实例,由内坑开挖所导致的土体开裂宽度达170 mm,最大地面沉降竟达300 mm。由此可见,内坑开挖对整个基坑的变形影响深重,应当引起重视。一些学者通过不同方式对内坑开挖引起基坑变形的特性进行了研究[7,8],获得了一些有益的成果。但是这些研究并没有考虑到大量坑中坑式基坑工程内坑开挖位置、深度、面积等因素的随机性,所有工程中的内坑不可能都出现在同一个位置。因此,有必要在充分考虑上述因素的情况下对内坑不同开挖位置、开挖深度、开挖面积时基坑的变形进行分析,以便探究内坑开挖影响下的坑中坑式基坑变形特性。
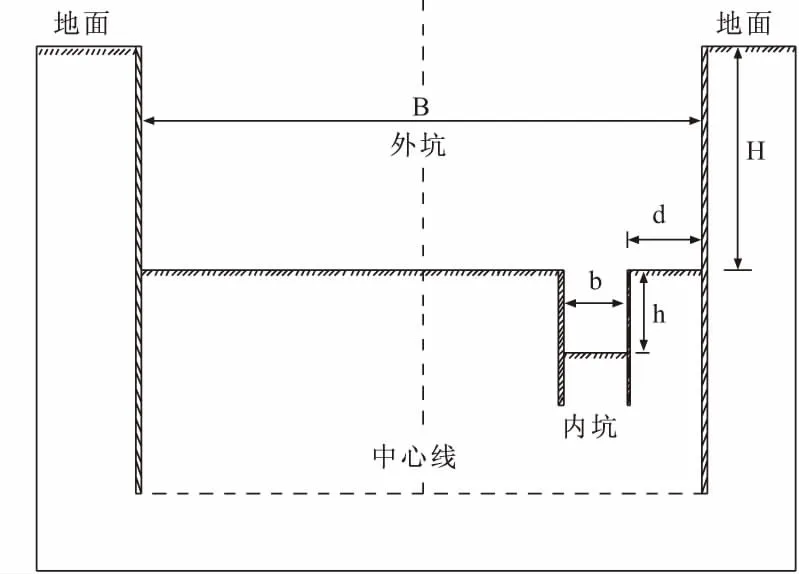
图1 坑中坑式基坑剖面
1 内坑开挖对外坑变形影响机制
内坑处于外坑围护结构的被动侧,内坑的开挖使得外坑被动土压力区土体卸载,围护结构外侧附近土体水平方向应力水平减小,而竖向应力保持不变。主被动区土压力平衡破环,应力重新分布,被动区土压力合力作用点降低,削弱被动区土体阻止围护结构侧移及转动的抗力,而抗力的丧失将直接导致墙体侧移增大,进而加剧墙体外侧地面的沉降。当内坑小而浅,离围护结构又较远时,内坑的开挖对被动区土压力分布的扰动较小,引起的围护结构侧向位移及地面沉降较小。当内坑深而大,距离围护结构又较近时,被动区土压力分布剧烈变化,主、被动区土压力失衡,将导致过大的围护结构侧向位移及地面沉降,严重的将导致基坑整体失稳破坏。
2 坑中坑参数及有限元模型

运用有限元软件ABAQUS进行数值模拟分析。ABAQUS拥有能够真实反映土体性状的本构模型,具有强大的接触面处理功能,能很好的模拟土与结构之间的相互作用,对岩土工程具有很强的适应性。

图2 有限元模型
为了便于分析,有限元模型暂考虑单一内坑的情况。土体简化成均质土体,参数如表1所示,其中修正剑桥模型参数由三轴压缩试验获取。坑中坑式基坑有限元模型如图2所示,挖深H=10 m,挖宽B=32 m。围护结构采用80 cm厚地下连续墙,插入外坑底部以下8 m,弹性模量E=20 GPa,混凝土支撑截面尺寸为80 cm×80 cm。内坑开挖前分三步开挖外坑土体:在0 m处设置第一道水平支撑,开挖至-3 m;设置第二道支撑,开挖至-6 m;设置第三道支撑,开挖至-10 m。土体采用CPE4单元,围护结构采用B21单元,支撑采用二维杆单元。内坑围护结构采用60 cm厚地下连续墙,弹性模量E=20 GPa。运用修正剑桥模型进行模拟。为尽量减小边界条件对计算结果的影响,模型坑外土体宽度方向延伸至距离外坑坑壁8H处,并约束两侧边水平方向位移,深度方向取4H,并约束底部水平和竖向两个方向的位移。

表1 土的参数
3 内坑开挖引起的外坑变形特性

图3~5为内坑开挖前各开挖步土体所产生的水平位移云图(模型右半部分),图6为内坑开挖前各步开挖所引起的围护结构侧移,图7为围护结构弯矩分布图,图8~10为内坑开挖前各开挖步土体竖向位移云图,图11为内坑开挖前各步开挖所引起的地面沉降曲线。

图3 第一步开挖土体水平位移

图4 第二步开挖土体水平位移

图5 第三步开挖土体水平位移

图6 各步开挖围护结构侧向位移

图7 围护结构弯矩分布

图8 第一步开挖土体竖向位移

图9 第二步开挖土体竖向位移

图10 第三步开挖土体竖向位移

图11 各步开挖地表沉降量
由图6、图7、图11可知:
(1)开挖深度对围护结构水平位移及地面沉降影响显著,随着深度的增加两者都显著增大。
(2)第一步开挖最大位移发生在开挖面之下,第三步开挖最大位移发生在开挖面之上附近,这可能与支撑具体位置及围护结构刚度有关。第一步开挖围护结构最大位移发生在-7m处,最大弯矩发生在-6 m处;至第三步开挖最大位移发生在-8 m处,最大弯矩发生在-9 m处。最大位移发生位置在最大弯矩发生位置附近,内力与变形情况相符。
(3)围护结构最大水平位移发生在地表以下0.7H~0.8H处,随着开挖深度增加,发生位置略有下降;地表沉降最大值发生在距坑壁约0.7H处,位置几乎不变,两者最大位移发生位置尺寸相当。
3.1 坑趾系数的影响

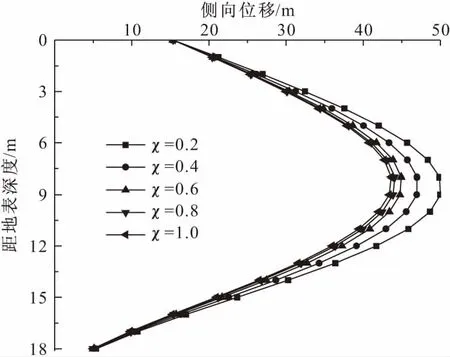
图12对围护结构水平位移的影响

图13对地表沉降量的影响

3.2 深度比的影响


图14 α对围护结构水平位移的影响
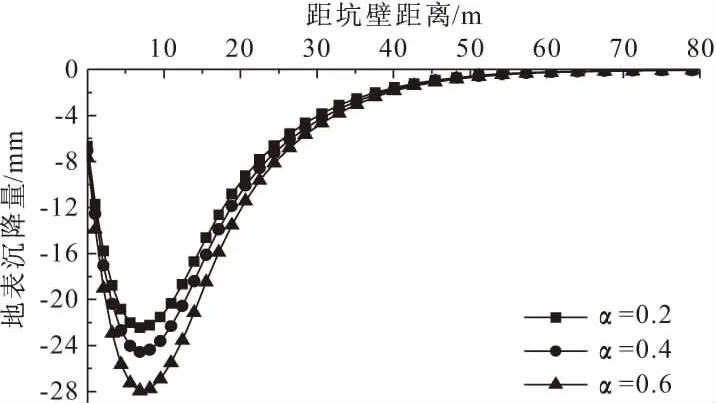
图15 α对地表沉降量的影响
由图14、图15可知围护结构水平位移及地表沉降量与深度比α呈正相关关系,α越大,外坑变形越大。由图3可知内坑开挖前围护结构最大位移为41.6 mm,α取值为0.2、0.4、0.6时,围护结构最大位移分别为43.2 mm、47.0 mm、53.3 mm,增幅依次为3.8%、13.0%、28.1%。由图6可知内坑开挖前,地表最大沉降量为21.6 mm,α取值为0.2、0.4、0.6时,地表最大沉降量分别为22.4 mm、24.6 mm、27.9 mm,增幅依次为3.7%、13.9%、29.2%。可见围护结构最大水平位移和地表最大沉降量随着α的增大都急剧增大,呈现“加速”增长趋势,当α=0.6时的增幅几乎与开挖一整层土产生的变形相当。分析可知,在离外坑壁较近的位置开挖深度较大的内坑时,本质上是减小外坑围护结构的有效插入深度,这对外坑抵抗侧向位移及地表沉降是非常不利的,同时这也是文献[2,3]寻求围护结构等效深度计算方法的初衷。工程实际中建议严格控制内坑的开挖深度,采取适当的内坑支护措施,或者在设计中加大外坑围护结构插入深度来改善深内坑开挖对外坑变形的不利影响。
3.3 面积比的影响

固定深度比α为0.4,面积比β取值分别为0.25、0.50、0.75,得到面积比影响下的围护结构水平位移及地表沉降曲线的变化,如图16、17所示。

图16 β对围护结构水平位移的影响

图17 β对地表沉降量的影响
由图16、图17可知面积比影响下,外坑的变形趋势与深度比的影响类似,随着β的增大,围护结构最大水平位移和地表最大沉降量都明显增大:当α由0.25增大到0.5时,围护结构最大水平位移增大3.2%,地表最大沉降量增大3.5%,而当α由0.5增大到0.75时,围护结构最大水平位移增大7.4%,地表最大沉降量增大7.7%。可见,面积比影响下外坑的变形也呈现“加速”增长趋势。经分析,面积比对外坑变形的影响机理可能与深度比的影响机理稍有差别:面积比的增大不仅能显著减小外坑围护结构的有效插入深度,而且大面积的垂向卸荷改变坑底原始应力状态,增大上下土面应力差(文献[4]也指出各因素中面积比对应力场扰动最大),使围护结构外围土体产生侧向剪切应变,增大围护结构侧向位移趋势,最终也导致坑外地表沉降增大。建议工程实际中,在不更改原有设计的情况下尽量缩减内坑的开挖面积,并做好内坑的支护措施,以达到抑制外坑变形增大的目的。
4 结 论
(3)较大的深度比将严重减小外坑围护结构的有效插入深度,对外坑的变形与稳定非常不利。
(4)大面积的内坑开挖不但减小外坑围护结构的有效插入深度,而且引起较大的外坑侧向剪切变形及地表沉降。
本文未讨论有限元模型参数变化对基坑变形特性的影响。笔者曾改变土的参数进行模拟,发现围护结构侧移及地表沉降具体大小有所改变,但最终分析得出的基坑变形特性与上述四点是相同的。
[1] 龚晓南. 关于基坑工程的几点思考 [J]. 土木工程学报, 2005, 38(9): 99-102.
[2] 吴铭炳,林大丰,戴一鸣,等. 坑中坑基坑支护设计与监测[J]. 岩土工程学报, 2006, 28(S1): 1570-1572.
[3] 徐意智,廖少明,周小华,等. 上海软土坑中坑型基坑围护的等效深度计算法 [J]. 岩土力学, 2012, 33(9): 2736-2742.
[4] 申明亮,廖少明,周小华,等. 坑中坑基坑应力场的参数化分析 [J]. 岩土工程学报, 2010, 32(S2): 187-191.
[5] 付文光,杨志银,刘俊岩,等. 复合土钉墙的若干理论问题、兼论《复合土钉墙基坑支护技术规范》 [J]. 岩石力学与工程学报, 2012, 31(11): 2291-2304.
[6] 徐为民,屠毓敏. 某工程坑中坑塌滑原因分析及加固设计 [J]. 岩土力学, 2010, 31(5): 1555-1559.
[7] 陈乐意,李镜培,梁发云,等. 坑中坑对基坑围护结构水平位移影响数值分析 [J]. 岩土工程学报, 2008, 30(S1): 59-61.
[8] 刘吉波,王 新. 某阶梯基坑内坑围护桩插入比优化研究 [J]. 水文地质工程地质, 2012, 39(5): 74-77.
