用量子理论分析均匀磁场中带电粒子的运动
2013-01-10李东康
李东康,李 佳
(通化师范学院 物理学院,吉林 通化 134002)
1 引言
在经典力学中,电荷量为q,质量为m的粒子,以初速度v0进入均匀磁场B中,如果v0与磁感应强度B相互平行,洛伦兹力等于零,带电粒子做匀速直线运动;如果v0与B相互垂直,带电粒子受到与运动方向垂直的洛伦兹力F=qv×B,方向垂直与v0及B,所以带电粒子速度大小不变,方向改变,切割磁感线做匀速圆周运动;如果v0与B斜交成θ角,v0分解成平行于B的分矢量和垂直于B的分矢量,两种运动合成为等距螺旋运动.基于带电粒子在均匀磁场中运动的规律,人们总结出在某些特定情况下带电粒子的运动规律,并广泛的应用于电真空器件.比如,磁聚焦应用于显像管中电子束的聚焦装置;利用电场和磁场分布的某种对称性,通过电磁力来控制带电粒子的运动而制成的速度选择器和用磁场和电场的各种组合来达到把电荷量相等但质量不同的粒子分离开来,研究同位素、测定荷质比的质谱仪,以及回旋加速器等.描述粒子在磁场中运动的理论,一个是上述的宏观经典力学,一个是微观的量子力学,本文中采用量子理论分析均匀磁场中带电粒子的运动,并讨论带电粒子在外磁场中的运动规律[1,2].
2 带电粒子在电磁场中的薛定谔方程
一个质量为u,荷电q的粒子在电磁场中运动,则电磁场中荷电q的粒子的Hamilton量表为:
因而带电粒子在电磁场中的薛定谔方程[2]为:
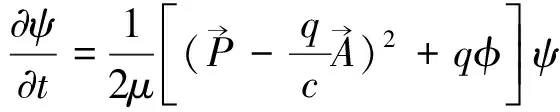
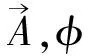
2.1 均匀外磁场中原子的塞曼效应
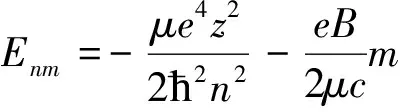
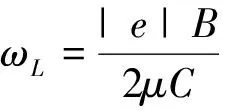
由上式可看到,外磁场的存在使能量本征值由En变为En+mħωL.没有外磁场时的能量本征值只取决于主量子数n,能级具有n2重简并.但当外磁场存在时,体系的能量不仅与n有关,而且还与磁量子数m有关.因此,原来对应于En的n个不同l,l=(0,1,2,…,n-1)的简并态能量不再是En,而是En+Em,其中m取2l+1个不同值,从而对给定的n,l能级分裂成2l+1条,简并被消除.每条能级间的能量间隔为:

在外磁场的作用下,原子能级的分裂现象叫做正常塞曼效应[3],而由于能级的分裂,原子的光谱线也发生分裂;当考虑电子的自旋时,在外磁场作用下能级分裂还与自旋有关,这时的能级分裂现象叫反常塞曼效应.
2.2 均匀的外磁场中的自由电子
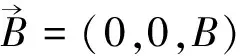
矢势

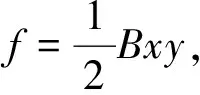
体系相应的Hamilton量可以写为:
(1)
将上式代入薛定谔方程:
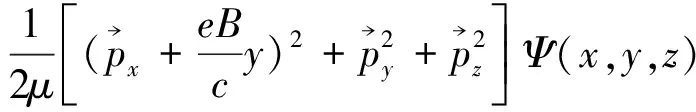
(2)
分离变量后,在y方向引入一常量y0,本征方程为:
(3)
由(3)我们可以看出,该方程为在平衡位置y=y0处的一维谐振子的能量本征方程.因此它的能量本征值为:

其中ω=2ωL,相应的能量本征值Eny的本征函数可写为:
其中,
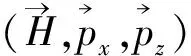
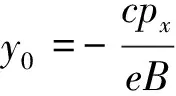
2.3 均匀外磁场中粒子的概率流密度
由概率流密度公式

得到该电子的概率流的密度为
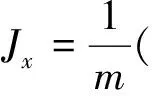
由于ψn(y)为实函数,所以
Jy=0.


得到(H,py,pz)的共同本征函数为:
由概率流密度公式:

得到该粒子的概率流密度为:

ħħ
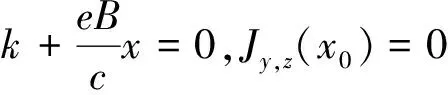
3 结论

参考文献:
[1]吴奇学.带电粒子在均匀磁场与三维各向同性谐振子场中运动的双波描述[J].物理学报,2000(7).
[2]曾谨言.量子力学导论[M].北京:北京大学出版社,1998:192-201.
[3]宋鹤山.量子力学[M].大连:大连理工大学出版社,2004:130-138.
[4]Leslie Ballentine.Quantum Mechanics:Amodern Development[M].Beijing:The world Book of Technology Press,1992:314-316.
