Application of regularized logistic regression for movement-related potentials-based EEG classification

Hu Chenchen Wang Haixian

(Research Center for Learning Science, Southeast University, Nanjing 210096, China)

Brain-computer interface (BCI) is a system to help patients with severe motor disabilities (e.g., amyotrophic lateral sclerosis, cerebral vascular accident and cerebral palsy) to express their intentions and manipulate the external environment. Moreover, it provides a new way of entertainment through which people can play electronic games without finger movement[1-5]. A variety of noninvasive technologies of electroencephalography (EEG), magnetoencephalography (MEG) and functional magnetic resonance imaging (fMRI) can be applied to BCI. Nevertheless, the EEG is commercially affordable and friendly operable. It also has excellent temporal resolution[6]. Our BCI research focuses on EEG signals.

The BCI system contains signal acquisition, preprocessing, feature extraction, feature selection and pattern matching that converts input signals into commands. The key point of BCI is signal processing, which has two purposes: feature extraction and classification. Current research typically uses features extracted by principal component analysis (PCA)[7], independent component analysis (ICA)[8], and common spatial pattern (CSP)[9]. The favorite classifications include linear discriminate analysis (LDA)[10], neural network (NN), and support vector machine (SVM)[11]. For the classification problem, the estimation of posterior probability plays an important role and the posterior probability can be directly used to predict labels of testing trials[12]. Logistic regression (LR) is a popular binary classification method based on the posterior probability and is often applied in EEG signal processing. The main advantage of LR is that it computes a probability value rather than a score and no prior feature extraction is required[13-14]. Meanwhile, the regression coefficients resemble CSP filters that transform original high-dimensional EEG data into a low-dimensional feature space which contains beneficial information for classification. However, LR is a global linear approach that ignores manifold information between different EEG trials. Besides, when few EEG trials contain outliers, the performance of LR may be deteriorated. Therefore, it is useful to incorporate the manifold regularization into LR[15].

The family of algorithms based on manifold learning[16], such as isometric map (ISOMAP), locally linear embedding (LLE), Laplace eigenmaps, and locality preserving projection (LPP)[17], is developed to preserve the topological structure of data points. In this paper, we combine the LPP regularizer term with sparse logistic regression (SLR)[18-19], called local sparse logistic regression (LSLR). The goal of the LSLR approach is to preserve the neighborhood information of original feature space in the framework of SLR. Computationally, to obtain the weighing vector, we use a bound optimization method with a component-wise update procedure. We demonstrate the effectiveness of our proposed method on an EEG-based BCI competition data set.

1 Methods

1.1 Sparse logistic regression

LetD={(X1,y1),…,(Xn,yn)}be a given data set.Xiis a raw EEG signal denoted by aT×Cmatrix, whereTis the number of recording time samples,Cis the number of EEG channels, andyi∈{-1,1} is the class label for thei-th input trial. In this paper,yi=1 andyi=-1 denote finger movement conditions of right hand and left hand, respectively. LR, considered in this paper, is a popular binary classification method[20]. The goal of LR is to determine the posterior probability of the occurrence of an event. The probability that thei-th trial belongs to classyiis

(1)

wherexidenotes aT×Cvector which is formed by straightening the elements ofXi;ωis a vector representing regression coefficients, each element of which corresponds to a weight of a feature. We estimate the weight matrix by maximizing the log-likelihood function:

(2)

While maximizingl(ω),regularization is constantly introduced to enable the weight vector to be sparse[21]. The popular regularizers are the LASSO term and the ridge term. The former is a sparse regularizer, which makes the weights of irrelevant features be zero; the latter enables the weights of relevant features to be larger and irrelevant features to be smaller without an exact tendency to be zero[19, 22-25]. However, the two regularizers might ignore the local structure of the EEG time course which contains discriminative information among patterns. To address this problem, we introduce a new regularizer and combine it with the SLR, which will be described in the next section.

1.2 Locality preserving logistic regression

1.2.1 Locality preserving projection

Locality preserving projection (LPP), a linear dimensionality reduction algorithm, is a useful and effective method for pattern recognition. It builds a projection to preserve the neighborhood structure of the original data based on Euclidean distances[17]. He et al.[26]showed that the LPP algorithm gave a better representation of the data structure and achieved higher accuracy in face recognition. Watanabe and Kurita[13]introduced the locality into the regularization term of LR and applied it to standard benchmark datasets. Some encouraging results were obtained[13, 27].

When defining the weight matrix, one usually introduces the following forms[28]:

1) 0-1 weighting:Qij=1 if and only if nodesiandjare connected by an edge.

2) Heat kernel weighing: If nodesiandjare connected,

(3)

whereτis a hyper parameter and it is usually determined by a cross validation strategy.

3) Dot-product weighing: If nodesiandjare connected,

(4)

Clearly, if ‖xi‖2and ‖xj‖2are both equal to 1,Qijis the cosine of the two vectors.

Owing to the tunable parameterτof the heat kernel weighing, we adopt the second form above to define the weight matrix.

1.2.2 LPP regularizer

In this paper, we propose the LPP regularizer as follows:

(5)

MinimizingELPPis an attempt to ensure that ifxiandxjare close in the original space, then they are close in the generation space. It gives a large value ofQijif the distance of two samples is close while it gives small weight when meeting distant samples. It shows the advantage of preserving the helpful neighborhood information of the original feature space.

By combining theELPPterm and the LASSO term, we obtain the log-likelihood function:

(6)

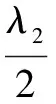
1.2.3 Bound optimization

With the bound optimization approach,l(ω) is optimized by iteratively maximizing a surrogate functionS,

(7)

(8)

whereg(ω) denotes the gradient ofl(ω). The matrixBof two classes is given by[19]

(9)

Adding the regularizers of LASSO and LPP, the surrogate function ofL(ω) is given by

(10)

By maximizing the surrogate function in the framework of bound optimization, we obtain the update equation:

(11)

(12)

(13)

soft(a;δ)=sign(a)max{0,|a|-δ}

(14)

From the theory of the bound optimization, we know that, with the above procedures, the value of the surrogate function monotonically increases at each iteration. The LSLR algorithm can be obtained in the following steps. First, we record the EEG data and do data preprocessing. Next, we initialize the parameters ofλ1,λ2,τ,ωoldand choose the best performance of the four parameters, respectively, by using cross-validation. Then we obtainωnewfromωoldby using Eq.(13) until ||ωnew|2-|ωold|2|<10-6.

2 Experiment

2.1 Self-paced finger tapping dataset

The self-paced finger tapping data set is an EEG data set from BCI competition 2003-dataset Ⅳ[29-31]. Our goal is to predict the type of upcoming finger movement before it really happens. The subject presses the corresponding keys at an average speed of once per second, using either the index finger or the little finger of the right or the left hand. The data set consists of 416 trials, in which 316 trials are used for training and the remaining trials are used for testing. The duration length of each trial is 630 ms, in which just the beginning 500 ms is adopted because the ending 130 ms mainly contains artifacts from the electro-myogram (EMG). The data contains 28 channels and is down sampled from 1 000 to 100 Hz.

2.2 Preprocessing

Before applying our algorithm, we use a band-pass Butterworth filter with cut-off frequencies from 7 to 35 Hz on the raw EEG data. Meanwhile, the temporal interval is selected as follows: We use the latter 200 ms time samples in the whole 500 ms because the data from this time window are more close to the real action, and have achieved higher classification accuracy than that of the whole 500 ms.

2.3 Experimental setting and results

In this experiment, we use classification accuracy to compare the results of SLR with LSLR. First, we select each element asλ1from the set {10-4,10-3,10-2,10-1,1,10,102,103,104} to test the accuracy of SLR because we found that when we fixed the value ofλ2, different values ofλ1made little difference in the accuracy of LSLR. Therefore, we test the accuracy of SLR with different values ofλ1first in order to find the best performance ofλ1. From Fig.1, we find that, when the value ofλ1is less than 10, the test accuracy changes slowly. Otherwise, it dramatically decreases. Then, on the basis of the optimalλ1, the same test is conducted on parameterλ2to do the LSLR experiment. The ten-fold cross-validation is used to evaluate the classification accuracy as follows. All the trials are divided into ten divisions, nine of which are used as the training set while the remaning one of which is used as the testing set. The average classifica-tion accuracy of the ten folds is considered as the final recognition rate. Tab.1 shows the performance of the LSLR method according to different values of theλ2penalty term.

Fig.1 Test accuracy of SLR vs. variation of parameter λ1

Tab.1 Average recognition values of SLR and LSLR using the ten-fold cross-validation

We find that LSLR outperforms SLR when we keep the value ofλ1invariant and select different values ofλ2. The optimal LSLR performance is significantly above the average performance using SLR according to a t-test paired by cross-validation runs (p<0.05). The improvement of classification performance comes from the local structure modeling of LSLR. However, the LPP regularizer yields a dense model whereas the LASSO term only selects 53.93% of the features. Fig.2 contains box plots that compare the difference between SLR and LSLR in terms of test accuracy. The result strongly shows that our method outperforms SLR.

Fig.2 Box plot of the accuracy using SLR and LSLR

Moreover, two other algorithms of LDA and LR are evaluated over the same dataset and the classification rates are demonstrated in Tab.2. CSP is used to extract features before applying LDA as a classifier.

Tab.2 Average recognition values of LDA, LR, SLR and LSLR

From Tab.2, it is noticed that the recognition values obtained by LDA and LR without regularization are low. The regularized logistic regression SLR and LSLR give better recognition rates than LR. Especially LSLR gives the best recognition rate for BCI competition 2003-dataset Ⅳ. These results prove that the LPP regularizer is effective for classification of neuroimaging data and the LPP regularizer can be a helpful regularizer.

Note that the recognition value of Wang et al.[31], the winner in this dataset, achieved 84%. The algorithm combines common spatial subspace decomposition with LDA to extract features, and then uses a perceptron neural network as the classifier. In our algorithm, no prior feature extraction is required and we directly use LSLR to classify a single-trial EEG during the preparation of self-paced tapping.

2.4 Discussion

The LASSO term produces a sparse solution while the LPP regularizer has desirable properties. From Tab.1 and Fig.2, the improvement of classification performance comes from the LPP term, which provides the advantage of preserving the helpful neighborhood information of original feature space with less outlier distortion. It defines a small weight if the distance of two samples is large while it puts a large weight when meeting near neighbor samples. In our experiment, our classifier of the regularized logistic regression contains the step of feature extraction.

3 Conclusion

The goal of this paper is to demonstrate that the LPP regularizer, which is beneficial to the classification, can preserve the neighborhood information of the original feature space. Compared with SLR, LSLR has better discriminate performance. Actually, LSLR is the extension to logistic regression. Experimental results indicate that LPP regularization is a valuable regularization in single trial EEG data. Our future direction is to explore more useful regularizers and test their performance in EEG-based BCI application.

[1]Bashashati A, Fatourechi M, Ward R K, et al. A survey of signal processing algorithms in brain-computer interfaces based on electrical brain signals [J].JNeuralEng, 2007,4(2): R32-R57.

[2]Wolpaw J R, Birbaumer N, Heetderks W J, et al. Brain-computer interface technology: a review of the first international meeting [J].IEEETransNeuralSystRehabilEng, 2000,8(2): 164-173.

[3]Birbaumer N, Ghanayim N, Hinterberger T, et al. A spelling device for the paralysed [J].Nature, 1999,398(25): 297-298.

[4]Kübler A, Kotchoubey B, Kaiser J, et al. Brain-computer communication: unlocking the locked in [J].PsycholBull, 2001,127(3): 358-375.

[5]Wolpaw J R, Birbaumer N, McFarland D J, et al. Brain-computer interfaces for communication and control [J].ClinNeurophysiol, 2002,113: 767-791.

[6]Haynes J D, Rees G. Decoding mental states from brain activity in humans [J].NatRevNeurosci, 2006,7: 523-534.

[7]Wold S, Esbensen K, Geladi P. Principal component analysis [J].ChemometricsandIntelligentLaboratorySystems, 1987,2(1/2/3): 37-52.

[8]Hyvarinen A, Karhunen J, Oja E. Independent component analysis: algorithms and applications [J].NeuralComputation, 2001,13(4/5): 411-430.

[9]Blankertz B, Tomioka R, Lemm S, et al. Optimizing spatial filters for robust EEG single-trial analysis [J].IEEESignalProcessingMagazine, 2008,25(1):41-56.

[10]Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels [C]//IEEESignalProcessingSocietyWorkshop. Madison, WI, USA, 1999:41-48.

[11]Cortes C, Vapnik V. Support-vector networks [J].MachineLearning, 1995,20(3): 273-297.

[12] Li T, Wang J, Wu X, et al. The estimate and application of posterior probability: based on kernel logistic regression [J].PatternRecognitionandArtificialIntelligence, 2007,19(6): 689-695.

[13]Watanabe K, Kurita T. Locality preserving multi-nominal logistic regression [C]//19thInternationalConferenceonPatternRecognition(ICPR 2008). Tampa, FL, USA, 2008: 1-4.

[14]Aseervatham S, Antoniadis A, Gaussier E, et al. A sparse version of the ridge logistic regression for large-scale text categorization [J].PatternRecognitionLetters, 2011,32(2): 101-106.

[15]Chen Z, Haykin S. On different facets of regularization theory [J].NeuralComputation, 2002,14(12): 2791-2846.

[16]Belkin M, Niiyogi P, Sindhwani V. Manifold regularization: a geometric framework for learning from labeled and unlabeled examples [J].TheJournalofMachineLearningResearch, 2006,7(12): 2399-2434.

[17]He X, Niyoqi P.Localitypreservingprojections[D]. Chicago, IL,USA: University of Chicago, 2005.

[18]Krishnapuram B, Carin L, Figueiredo M A T, et al. Sparse multinomial logistic regression: fast algorithms and generalization bounds [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005,27(6):957-968.

[19]Ryali S, Supekar K, Abrams D A, et al. Sparse logistic regression for whole-brain classification of fMRI data [J].Neuroimage, 2010,51(2): 752-764.

[20]Bielza C, Robles V, Larranaga P. Regularized logistic regression without a penalty term: An application to cancer classification with microarray data [J].ExpertSystemswithApplications, 2011,38(5): 5110-5118.

[21]Poggio T, Girosi F. Regularization algorithms for learning that are equivalent to multilayer networks [J].Science, 1990,247(4945): 978-982.

[22]Cawley G C, Talbot N L C, Girolami M. Sparse multinomial logistic regression via Bayesian l1 regularisation [C]//AdvancesinNeuralInformationProcessingSystems. Vancouver, CA, USA, 2007.

[23]Meier L, Geer S V D, Buhlmann P. The group lasso for logistic regression [J].JournaloftheRoyalStatisticalSociety:SeriesB, 2008,70(1): 53-71.

[24]Zou H, Hastie T. Regularization and variable selection via the elastic net [J].JournaloftheRoyalStatisticalSociety:SeriesB, 2005,67(2): 301-320.

[25]Tomioka R, Müller K R. A regularized discriminative framework for EEG analysis with application to brain—computer interface [J].Neuroimage, 2010,49(1): 415-432.

[26]He X, Yan S, Hu Y, et al. Face recognition using Laplacianfaces [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005,27(3): 328-340.

[27]Kurita T, Watanabe K, Otsu N. Logistic discriminant analysis [C]//IEEEInternationalConferenceonSystems,ManandCybernetics. San Antonio, USA, 2009: 2167-2172.

[28]He X, Cai D, Shao Y, et al. Laplacian regularized Gaussian mixture model for data clustering [J].IEEETransactionsonKnowledgeandDataEngineering, 2007,23(9): 1406-1418.

[29]Blankertz B, Curio G, Müller K R. Classifying single trial EEG: towards brain computer interfacing [C]//AdvancesinNeuralInformationProcessingSystems. Vancouver, CA, USA, 2002: 157-164.

[30]Wang H X, Xu J. Local discriminative spatial patterns for movement-related potentials-based EEG classification [J].BiomedicalSignalProcessingandControl, 2011,6(5): 427-431.

[31]Wang Y, Zhang Z, Li Y, et al. BCI competition 2003-data set Ⅳ: an algorithm based on CSSD and FDA for classifying single-trial EEG [J].IEEETransBiomedEng, 2004,51(6): 1081-1086.