基于遗传蚁群算法的云资源调度问题研究

金 瑾, 何 嘉

(成都信息工程学院计算机学院,四川成都610225)

0 引言

云计算是近年新兴的一种网络应用模式。是集网格计算、分布式计算、并行计算、效用计算、网络存储、虚拟化、负载均衡等传统计算机技术和网络技术为一体,再互相融合的产物。云计算的核心思想:将大量用网络连接的计算资源统一管理和调度,从而构成一个计算资源池。像电力资源一样,用户只需提出所需,云计算就能够向提供方便快捷的服务。因此如何快速合理地对网络资源进行调度是云计算需要解决的关键问题,它关系到云资源环境所能提供服务的好坏。

传统的资源调度算法有轮询算法(RR),基本ACO算法等,RR算法的原理是每一次把来自用户的请求轮流分配给内部中的服务器,从1开始,直到N(内部服务器个数),然后重新开始循环。它不考虑服务器的状态(即不关心当前服务器的连接数和响应速度),因此当请求服务间隔时间变化比较大时,轮询调度算法容易导致调度不平衡。目前的资源调度策略大多数是通过虚拟机级别上的调度技术结合一定的调度策略为虚拟机内部应用做资源调度[1],例如文献[2]针对计算集群中的虚拟机调度进行建模,根据虚拟机的负载动态调节处理器电压,文献[3-4]通过动态分配云计算数据中心的虚拟机,减少服务器的个数,文献[5]给出基于门限的云计算资源动态调度方法,文献[6]提出基于博弈论的云计算资源分配算法。这些资源调度方法虽在一定程度上提高了源调度的效率,然而面对数量庞大的资源时却时常会遇到瓶颈,而智能算法的各方面优点表明其对于像云资源调度类的调度问题显示出一定的优越性。

蚁群算法是20世纪90年代初意大利的M.Dorigo等学者提出的[7],与遗传算法、粒子群算法等智能算法一样,蚁群算法是模拟现实世界中真实蚂蚁的觅食行为而形成的一种模拟进化算法,这些学者们充分利用蚁群搜索食物的过程与旅行商问题之间的相似性,解决了TSP问题,取得了很好的结果。大量的实验结果还证明蚁群算法的有效性和在某些领域的优势[8-9]。同时,蚁群算法也存在一定的缺陷,即搜索时间过长和容易陷入局部较优解[10],蚁群算法在动态环境下也表现出高度的灵活性和健壮性,成功解决了许多组合优化问题。云计算中的任务调度问题,实质上是一种寻找较优解的问题,即,从资源分配给任务的多个解中选出较优解的一种过程,从解决问题角度看,蚁群优化算法非常适合解决云环境中的资源调度问题[11]。

1 基本蚁群优化算法的原理

以MMAS应用于TSP问题的求解为例阐述基本蚁群优化算法的原理[12-15]。

为了便于描述问题,首先引入以下符号:m:蚂蚁数量,dij(i,j=1,2,…,n):城市之间的距离;τij(t):t时刻在城市i,j连线的残留信息量,一般取τij(0)=C(C常数);ηij:t时刻蚂蚁由城市i转移到城市j的启发信息,一般取;即信息素的大小为两城市距离的倒数。

pij(t):t时刻蚂蚁由城市i转移到城市j的概率,计算公式为:

其中reallowedk表示蚂蚁k下可走的城市集,它是动态变化的,因蚂蚁k的进程而改变;信息量 τij(t)会逐渐衰弱,1-p:衰减程度;α:蚂蚁所积累的信息量(在运动过程中),β:启发式因子所起的不同作用(在蚂蚁选路的过程中);

蚁群算法的步骤:

(2)蚂蚁根据公式(1)选择所要走的下一个城市,并修改 tabuk;

(3)每只蚂蚁走完一条边后,按式 τij(t+1)=(1-ρ).τij(t)+ρ Δτkij更新该边的信息素,其中 Δτkij=Q/lp,其中lp是蚂蚁从初始位置到当前城市走过的路径长度。ρ表示信息的持久性。对于所有边(i,j)限制 τij(t)∈[τmin(t),τmax(t)];超出这个范围的值被强制设为 τmax或者是 τmin。这样做可以使信息素较为平均,防止信息素大小两极分化,从而使算法更好地寻优;

(4)计算最佳路径。当全部蚂蚁走完所有城市后,按下面式计算最优路径的长度并且保留,

lmin=minlk,k=(1,2,…,m),其中 lk:第k只蚂蚁所走路径长度;

(5)经过n个时刻。蚂蚁k一次循环结束,即所有的城市都走完一遍。此时,要根据下式对这一轮遍历的全局最优路径上的信息量作一些更新::全局信息素挥发系数,lk:最优路径长度;

(6)如果设置的迭代次数未完,则清空禁忌表,重复上述过程。

2 GA-ACO与云计算资源调度

2.1 问题描述

采用所提出的GA-ACO算法寻找当前策略中的最优或较优的策略。由于云计算环境的特殊性和复杂性,需先对云资源调度问题与传统的应用蚁群算法的TSP问题进行关联,以供改进蚁群算法来适合云资源调度问题的使用[16],云资源调度问题与传统的TSP问题的差异主要体现在以下3个方面:

(1)在TSP问题中,城市之间会有固定的拓扑结构。而云环境中的资源并不是固定不变的,所以也不存在固定的网络拓扑结构。

(2)在TSP问题中,城市之间的信息素用城市之间的距离的倒数表示。而在云计算环境中则需要用资源的通信能力和计算能力等相关系数表示信息素。

(3)启发信息也起着非常重要的作用,在云环境中,需要以资源固有属性(如计算和通信能力)表示在蚁群算法中的启发信息。

把云计算资源调度的问题描述如下:设有 T个需要执行的任务,P个可用的资源。用集合表示为:任务集合T={T1,T2,…,Tn};资源集合 P={P1,P2,…,Pm};用 Ti表示第i个子任务,Pj表示第j个处理机资源。资源调度就是将n个子任务分配给m个处理机资源,从而使所有任务的完成时间最短,资源的利用率最高。

云资源调度的目标即是求(2)式的最小值[17]:

(2)式中,∑imi=M,M是给定时间内交给云计算环境的总任务量,mi表示资源i上分配mi个任务,0≤表示资源i上反能执行的最大任务并行数。

2.2 GA-ACO算法及在云资源调度中的应用

设第i个资源的处理能力为Pi,资源负载平衡能力为Li,任务节点与调度节点的通信能力为Ci,则每个资源的初始信息素表示为:τi(0)=α Pi+βCi+θ Li,其中 α,β,θ表示资源的处理能力初始化因子、资源节点间通信能力初始化因子和负载平衡能力初始化因子。

t时刻,第i个蚂蚁选择资源j的概率由下面的公式确定:

基中参数α 1代表信息素的重要程度,β1代表资源属性的重要程度,τj(t)表t时刻资源j的信息素浓度,ωu表示能见度因素。

遗传算法的全局搜索能力很强,但是局部搜索能力较弱[18],此算法运算简单,收敛速度快,但是求解到一定程度时往往出现收敛停滞现象。而蚁群算法采用正反馈原理[19],加快了进化速度,但是其全局搜索能力较差,容易限入局部解。两个算法优缺点具有互补的特性。文中所提出的GA-ACO算法即是将遗传算法和蚁群算法进行交叉融合,从而克服各自的缺点,达到较好的优化性能。GA-ACO算法对于蚁群算法的每个解,用局部搜索算法来精炼,并更新每个资源的信息素。然后,用GA算法的进化算子进化出新的解,再利用MMAS的转移概率建立GA算法的交叉算子。

GA-ACO算法步骤如下:

(1)初始化 nk个解;

(2)对每个个体的解 xk(k=1,2,…,nk)执行局部搜索;根据(1)式对更新信息素;

(3)对于 k=1,2,…,nk/2,随机选择两个父代 xa和xb,对 xa和xb进行交叉操作得到x′,如果 U(0,1)≤pm,则对 x′进行变异;

(4)用子代代替群体中较差的那一半;再根据(1)式更新信息素。

(5)若迭代未完成,则一直重复上述步骤,直到迭代完成。

其中交叉算法如下:

输入:xa和xb

令 x′=xa;

For所有的(i,j)∈x′and(i,j)∉xb

do从 x′中删除(i,j);

End

基于公式(3)连接各个部分。

3 仿真实验结果与讨论

所做的算法应用于云计算资源调度中,因此分别用MATLAB软件和云计算仿真软件(cloudsim)进行仿真。MATLAB软件是常用的仿真软件,具有用法灵活、程式结构性强、延展性好等优点,自带了很多智能计算的工具箱,方便进行计算机仿真。而CloudSim是一个新的、通用的和可扩展的仿真框架,用于新的云计算基础设施和应用服务的无缝建模、仿真和试验。

为验证GA-ACO算法的收敛性,用ACO算法与GA-ACO算法在MATLAB仿真平台下的收敛性进行对比,结果如图1和图2所示。GA-ACO算法当迭代次数为100次时,其精度为10-5,而基本的ACO算法迭代资数为3000次时精度不足10-2。实验结果表明,改进后的GA-ACO算法收敛度和精度相较于ACO算法都有所提高。

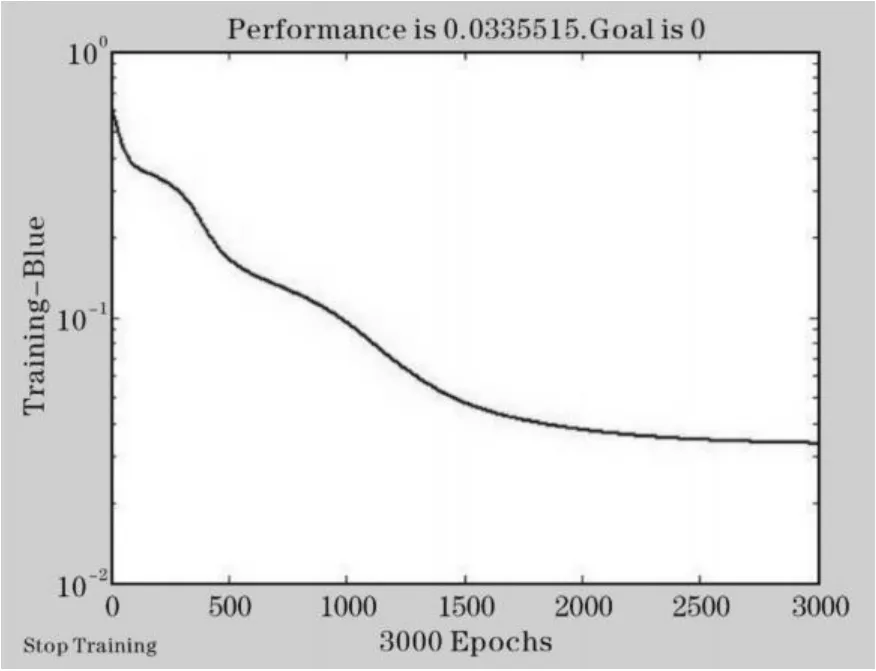
图1 ACO算法的性能

图2 GA-ACO算法的性能

另外,采用CloudSim仿真平台验证改进算法相较于其它调度算法的优越性,用云资源调度算法中传统算法轮询调度算法(RR)、ACO算法及GA-ACO算法分别进行调度。实验主要参数取值为:时间长度 T为24小时,利用率阈值为80%,预测时间间隔为200s,改进蚁群算法中 α为1,β为4,ρ为0.5,蚂蚁数量为80,最大迭代次数为120。假定数据中心有50台宿主机,CPU数在[1,5]内随机产生,MIPS为800,虚拟机所需CPU数为1,MIPS在[100,900]内随机产生,实验的任务数量分别是[50,100,150,200,250,300,350,400]。实验结果如图3所示,当任务数量250时,GA-ACO算法相的平均时间比ACO和RR算法分别少50和100s,而且随着任务数量越来越多,改进的GA-ACO算法后期随着信息素的增加,正反馈性增强,时间增加的幅度要远小于RR和ACO算法。因此所提出的GA-ACO算法在任务数量较多的时候执行效率要高,而执行时间要短。

图3 任务执行的平均时间对比

4 结束语

利用遗传算法对蚁群算法进行改进,并且引入最大最小蚁群算法对基于蚁群算法进行优化,从而使两种算法融合,改善原来算法的缺陷。形成新的GA-ACO算法,用实验讨论了新算法的精度和收敛度,相较于基于的ACO算法,新算法的精度和收敛度都有显著的提高,结合云计算资源调度的一些特点,将新算法应用于云资源调度中,与传统算法相比,新算法大大缩短了任务的平均运行时间,提高了资源的利用效率。

[1] Ge R,Feng X,Cameron K.Performance-constrained distributed dvs scheduling for scientific applications on power-aware clusters[A].Proceedings of the 2005 ACM/IEEE conference on Supercomputing[C].IEEE Computer Society,Washington DC,USA,2005:34-35.

[2] Von L G,Wang L,Younge A J,et al.Power-Avare Scheduling of Virtual Machines in DVFS-enabled Clusters[A].Proc.Of IEEE International Conference on Cluster Computing 2009[C].New Orleans,LA,USA,2009:1-10.

[3] Beloglazov A,Abawajy J,Buyya R.Energy-Aware Resource Allocation Heuristics for Efficient Management of Data Centers for Cloud computing[J].Future Generation Computer Systems,2012,28(5):755-768.

[4] Buyya R,Beloglazov A,Abawajy J.Energy-Efficient Management of Data Center Resources for Cloud Com-puting:A Vision,Architectural Elements,and Open Challenges[C].Proceedings of the 2010 International Conference on Parallel and Distributed Processing Techniques and Applications(PDPTA2010),Las Vegas,USA,July 2010:215-224.

[5] Lin Wei-Wei,Wang J Z,Liang Chen.et al.A Threshold-based Dynamic Resource Allocation Scheme for Cloud Computing[J].Procedings Engineering,2011,23(8):695-703.

[6] Wei Gui-yi,Visilakos A,Zheng Yao,et al.A gametheoretic method of fair resource allocation for cloud computing services[J].The Jounal of Supercomputing,2010,54(2):252-269.

[7] Dorigo M,Maniezzo V.Colorni A.Ant system:optimization by a colony of cooperating aigents[J].IEEE Transactions on SMC,1996,26(1):29-41.

[8] Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutional Comutation,1997,1(1):53-66.

[9] Dorigo M,Gambardella L M.A study of some properties of ant-Q[A].Voigt H-M,Ebeling W,Rechenberg I,etal.Proceedings of the PPSN 44th International Conference on Parallel Problem Solving from Nature[C].Berlin:Springer-Verlag,1996:656-665.

[10] Dorigo M,Maniezzo V,Colorni A.Ant system:an autocatalytic optimizing process[J].Tech Rep,1991:91-106.

[11] 王天擎,谢军,曾洲.基于蚁群算法的网格资源调度策略研究[J].计算机工程与设计,2007,28(15):3611-3613.

[12] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005:385-390.

[13] 谭营.计算群体智能基础[M].北京:清华大学出版社,2009:263-265.

[14] 王永贵,韩瑞莲.基于改进蚁群算法的云环境任务调度研究[J].计算机测量与控制,2011,19(5):1203-1211.

[15] 曹文梁,康岚兰.基于遗传算法的混合蚁群算法及其在TSP中的应用研究[J].2011,33(1):91-93.

[16] McKerrow P.Modelling the dragan-f lyer Four-Rotor Helicopter[A].Proceedings of IEEE International Conference on Robotics Automation[C].2004:3596-3601.

[17] 李士勇.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004:101-108.

[18] RowlinsG,ed.Foundations of Genetic Algorithm[J].Los Altos Morgan Kan fmann,1991:767-777.

[19] C M White,G G Yen.A Hybrid Evolutionary Algorithm for TSP[J].In Proceedings of the IEEE Congress on Evolutionary Computation.2004,12(2):1473-1478.