修正的Benjamin-Bona-Mahoney方程的精确解
2013-01-05皮金鑫周钰谦刘世杰
皮金鑫, 周钰谦, 刘世杰
(成都信息工程学院数学学院,四川成都610225)
0 引言
非线性方程的精确解对于理解非线性模型的物理意义起到很重要的作用,所以求解非线性方程的精确解在非线性问题中越来越重要。最近,对求解非线性方程的精确解提出了许多新的方法:如齐次平衡法[1],Backlund变换方法[2],双曲正切函数展开法[3],截断的Painleve展开法[4],Jacobi椭圆函数展开法[5],tanh函数展开方法及其推广方法[6-9]等。特别是王明亮提出的展开法[10],是一种更为简洁高效求得非线性方程精确解的方法。
研究的修正的Benjamin-Bona-Mahoney(BBM)方程[11]

其中参数α为非零的实数。该方程是许多不同物理系统中出现的弱非线性色散介质中长波单向传播的一个重要模型方程[12]。
1 预备知识
考虑非线性发展方程

其中,x,t为自变量,F为u及u的各阶偏导数的多项式。为了得到方程(2)的行波解,考虑一般的行波变换u(x,t)=U(ξ),ξ=x+ct,则方程可化为

设方程(3)的解具有以下形式

其中,G(ξ)满足二阶常微分方程

由方程(5)易得,当 G′(ξ)≠0时,
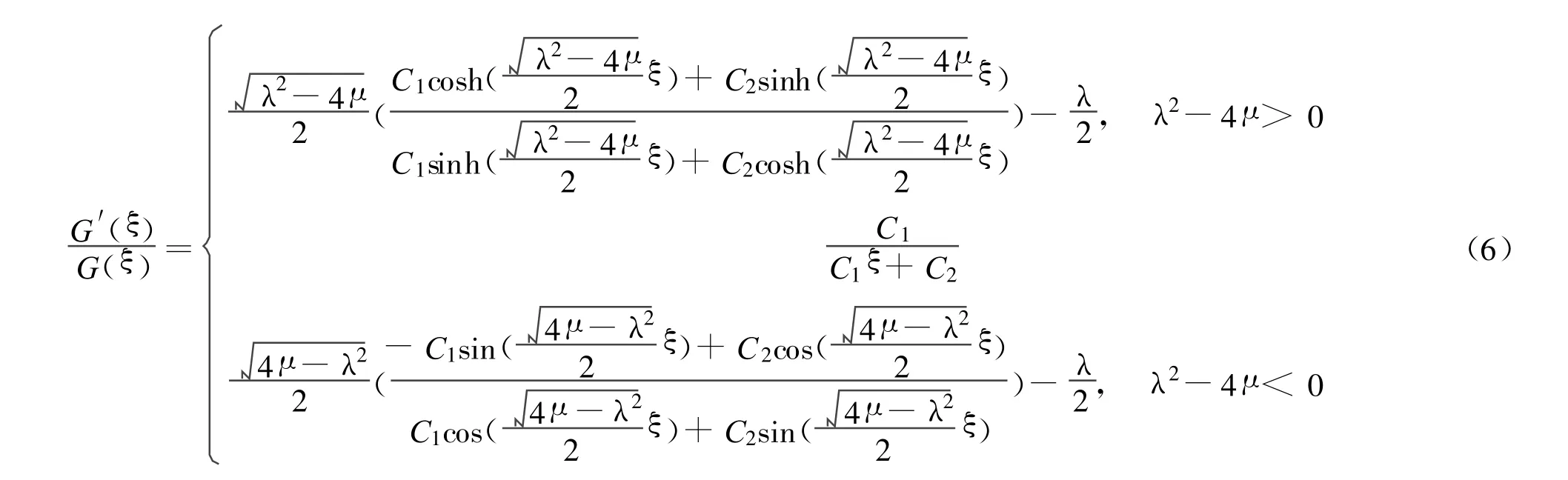
首先,对方程(1)作行波变换
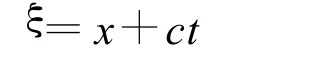
令 u(x,t)=U(ξ),则方程(1)可化作

平衡方程(7)中的最高倒数项U‴和非线性项U2U′,得到平衡系数n=1,由方程(4),则取

将解(8)带入方程(7)中,得到方程(7)中的各项为
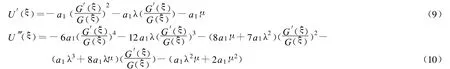
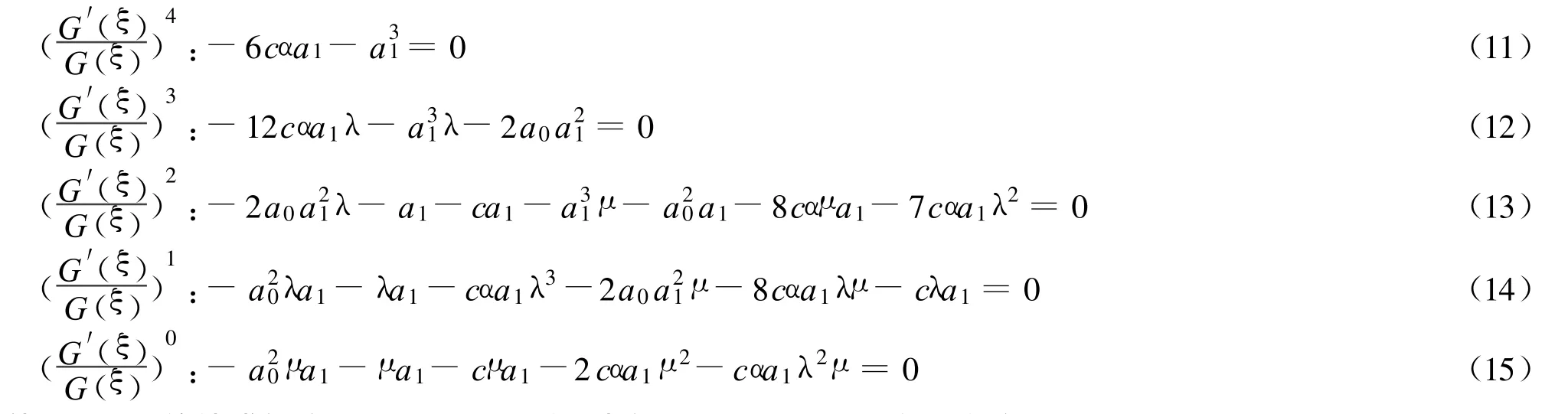
利用Maple软件求解方程(11)~(15),得到关于 a0,a1,c,λ,μ的一组解:
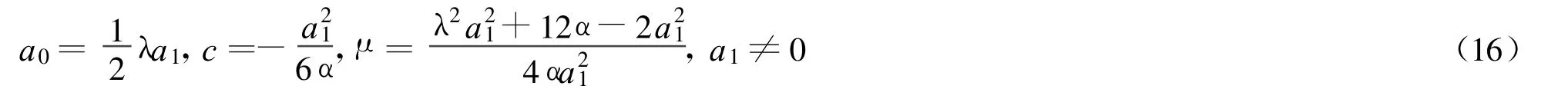
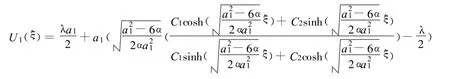
为了更好的理解 λ2-4μ>0时得到的这组孤子解,考虑到相关条件a1≠0,不妨取a1=1,α=,则作出解的数值模拟图如图1所示。
(ⅱ)当 λ2-4μ=时,
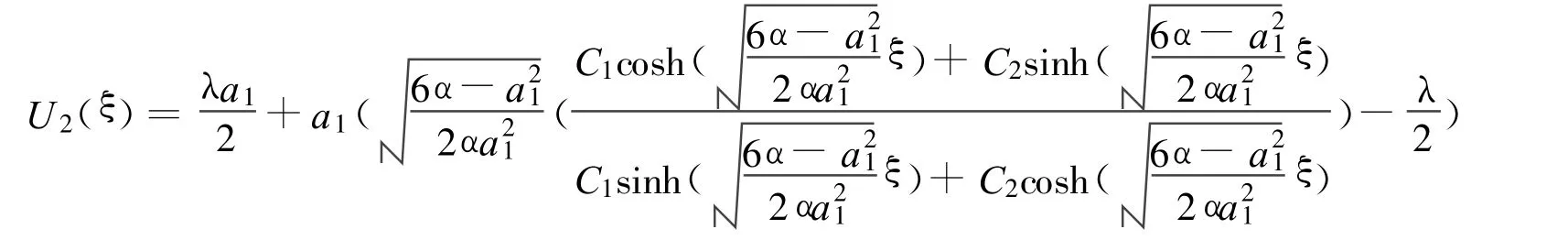
与(1)一样,用同样的方法对此解作数值模拟图。取a1=1,α=1,λ=1,C1=1,C2=1,则,作出解的数值模拟图如图2所示。
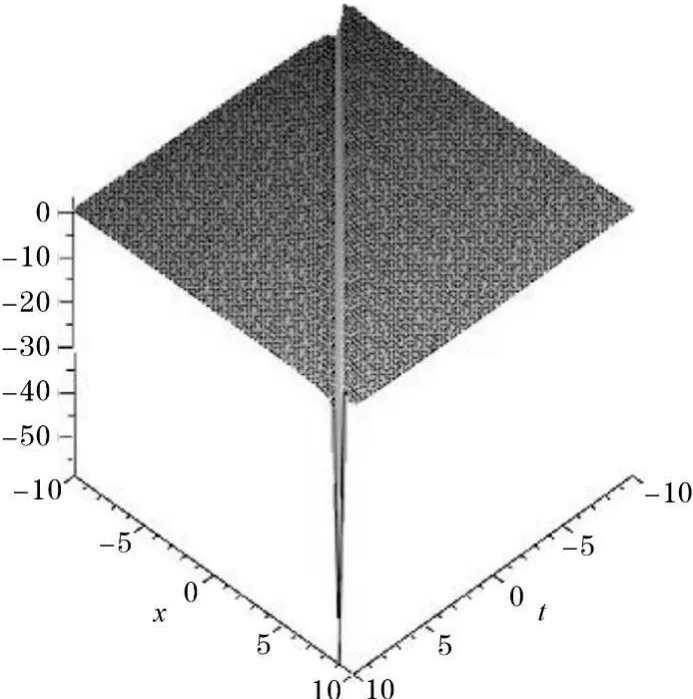
图1 λ2-4μ>0
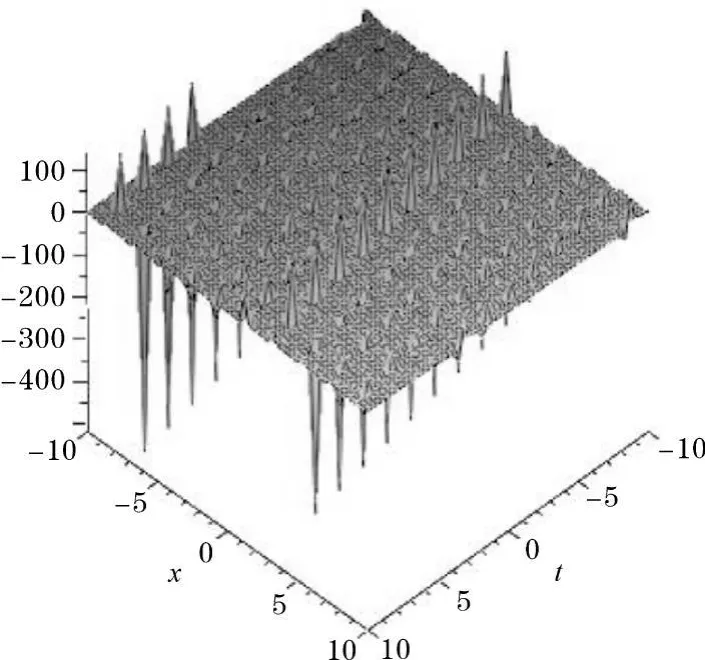
图2 λ2-4μ<0
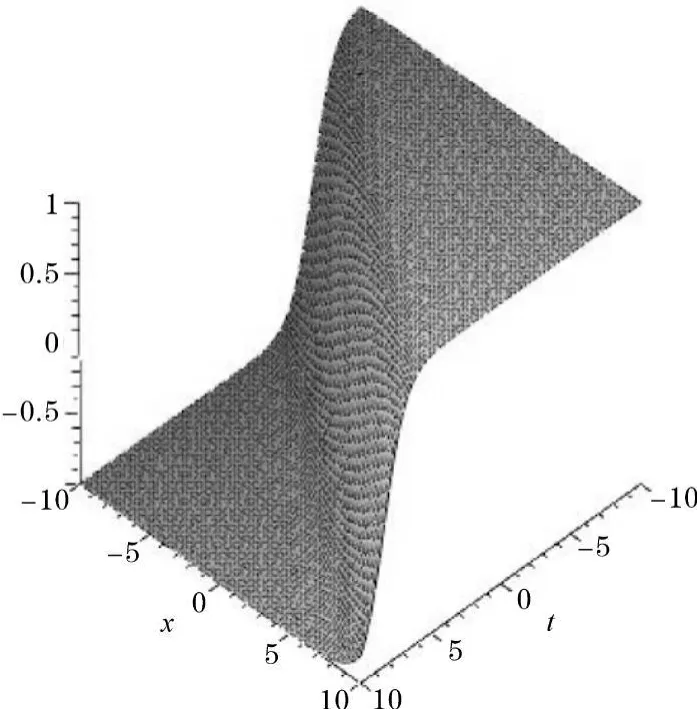
图3 λ2-4μ<0
3 结束语
[1] Wang M L.Solitary wave solutions for variant Boussinesq equation[J].Physics Letter A,1995,199:169-172.
[2] Yang L,Liu J,Yang K.Exact solutions of nonlinear PDE nonlinear transformations and reduction of nonlinear PDE to a quadrature[J].Physics Letter A,2001,278:267-270.
[3] 李志斌,张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报,1997,17(1):81-89.
[4] 范恩贵.可积系统与计算机代数[M].北京:科学出版社,2004.
[5] Parkes E J,Duffy B R.Traveling solitary wave solution to a compound KdV-Burgers equation[J].Physics Letters A,1997,229:217-220.
[6] 刘式适,付遵涛,刘式达.变系数非线性方程的Jacobi椭圆函数展开解[J].物理学报,2002,51:1923[7]Parkes E J,Duffy B R.An automated tanh-function method for finding solitary wave solutions to non-linearevolution equations[J].Computer Physics Communication,1996,98:288-300.
[8] 王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报,1999,98:8-16.
[9] Fan E G,Zhang H Q.New exact solutions to a system of coupled equation[J].Physics Letter A,1998,245:389-392.
[10] Wang M L,Li X Z,Zhang J L.The-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letter A,2008,372:417-423.
[11] 套格图桑,斯仁道尔吉.BBM方程和修正的BBM方程新的精确孤立波解[J].物理学报,2004,53:4052-4060.
[12] 龚伦训.修正的BBM方程的一些新精确解[J].原子与分子物理学报,2006,23:725-728.
