关于微积分学几个性质的探讨
2013-01-04司志本
司志本,李 蕊
(1.河北民族师范学院,河北 承德 067000 2.兴隆县青少年活动中心,河北 兴隆 067300)
在微积分学中,微积分的一些基本性质,给我们的计算或证明带来许多方便。但是,在学习这部分内容时,我们不能只满足于对已有性质的运用,还应该有意识的对一些性质做出进一步的探讨,挖掘其深刻的内涵.只有这样,才能使我们更好地掌握微积分学这部分内容。本文先讨论几个性质,然后再针对性质4举几个例子,说明这个性质在定积分的计算中所发挥的作用。
性质1 若函数f(x)为连续函数,则

性质1说明,对于一个可积函数f(x)来说,先求不定积分然后再求导,最后结果仍然是原来的函数f(x),也就是说,“求积分”和“求导”这两种运算的作用相互抵消了。性质1是微积分学中最简单、最基本的性质之一。在随后学习定积分时我们发现,积分上限函数有与(1)式类似的性质,即有下面的性质2.
性质2 若函数f(x)在[a,b]上连续,则积分上限函数在[a,b]上可导,而且有

比较(1)、(2)两式,我们发现
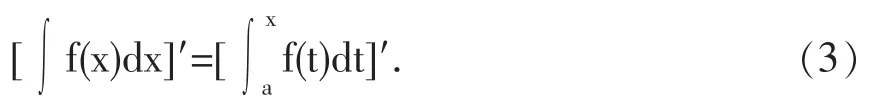
不难说明,如果把(1)式和(2)式中的x都换为x2,那么等式就不再成立。但是,我们有下面的(4)式和(5)式成立:
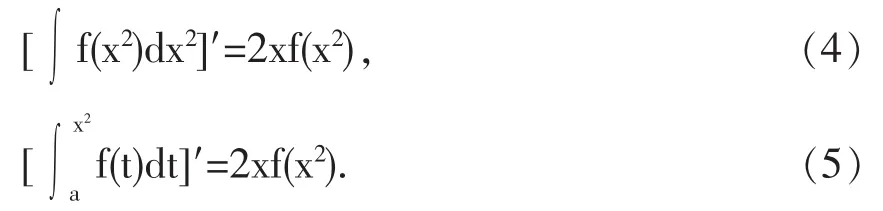
(4)式和(5)式都可以运用复合函数的求导法则进行证明。此处从略。
比较(4)式和(5)式,我们发现
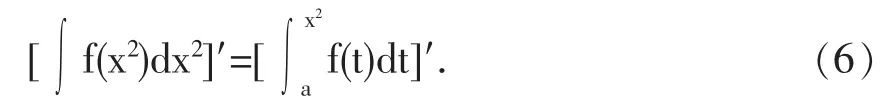
一般情况,对于任意的正整数n,有
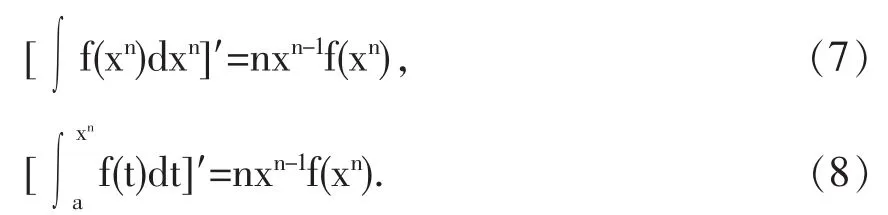
从而有
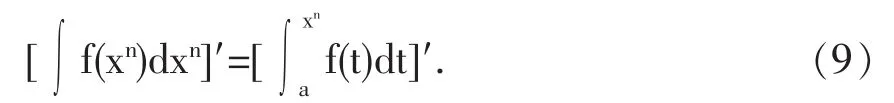
不难证明,(9)式当n是负整数时也成立,这样就得到下面的性质3.
性质3 对于任何可积函数f(x)以及非零整数n,都有
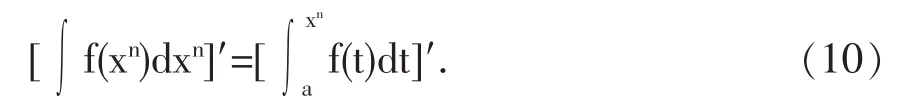
公式(10)把不定积分、定积分以及导数这三个概念有机的结合在一起,充分揭示了微分与积分的内在联系。
性质4 若f(x)为连续函数,则
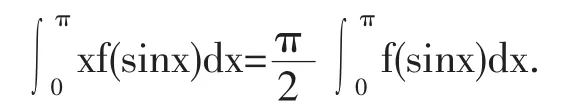
证明:设 x=π-t,则 dx=-dt,当 x=0 时,t=π;当 x=π 时,t=0.所以有

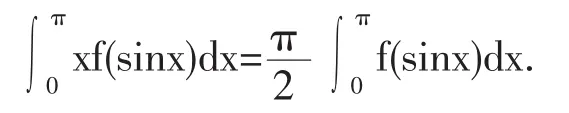
利用性质4,我们可以计算一类与之相关的定积分.
解:显然,被积函数f(x)=sinx在区间[0,π]上是连续的。由性质4可得


说明:上面例2在求积分的过程中,我们先把被积函数中的cos2x换成了1-sin2x,然后运用性质4,在用完性质4以后,又把1-sin2x还原为cos2x.这种循环变换有没有必要呢?实际上,因为cos2x=1-sin2x,所以,若被积函数f(x)的表达式中含有cos2nx,则不用做上面的循环变换,直接用性质4即可.例如,上面的例2也可以如下求解:
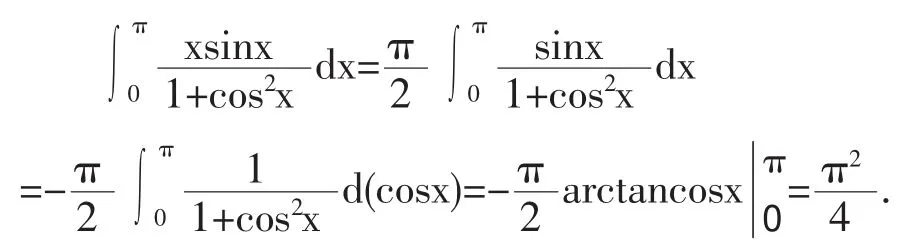
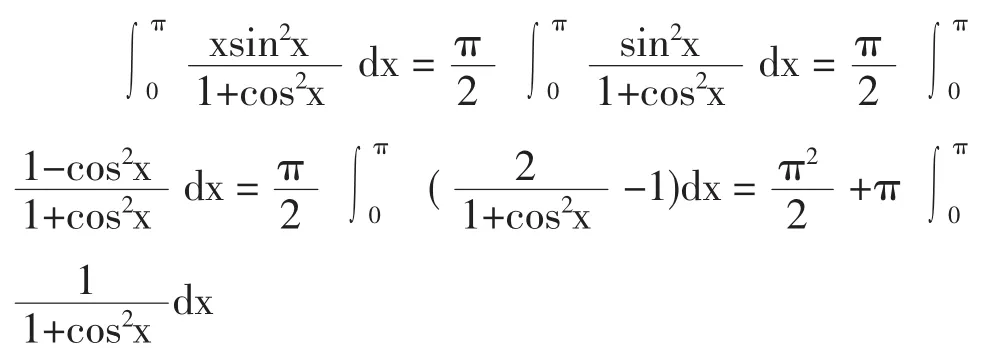
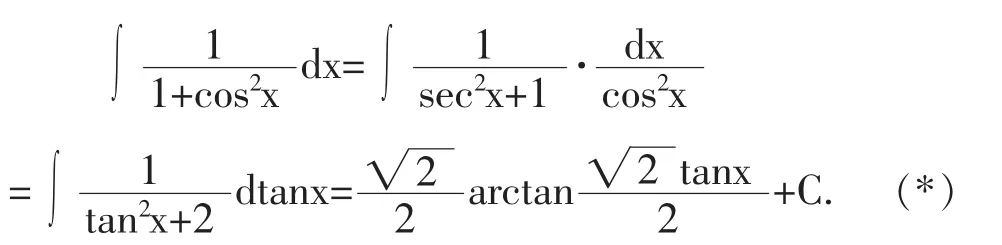
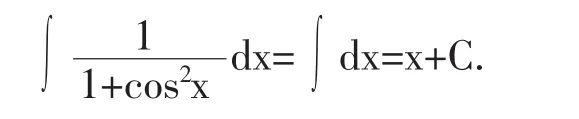
因为
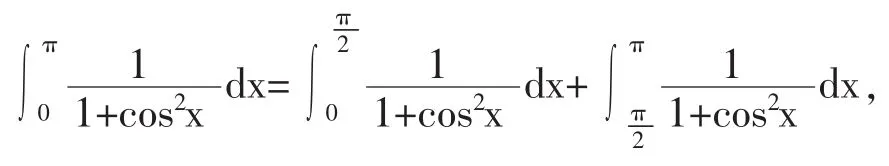

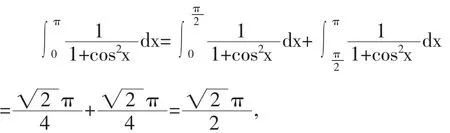
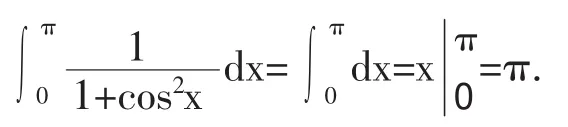
所以,原积分为
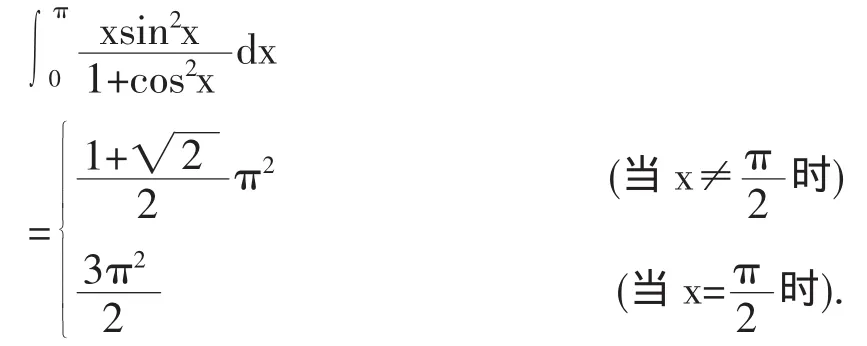
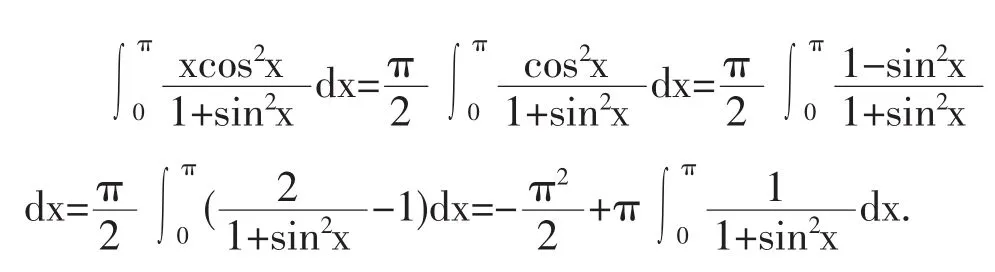
当 x≠0时,有
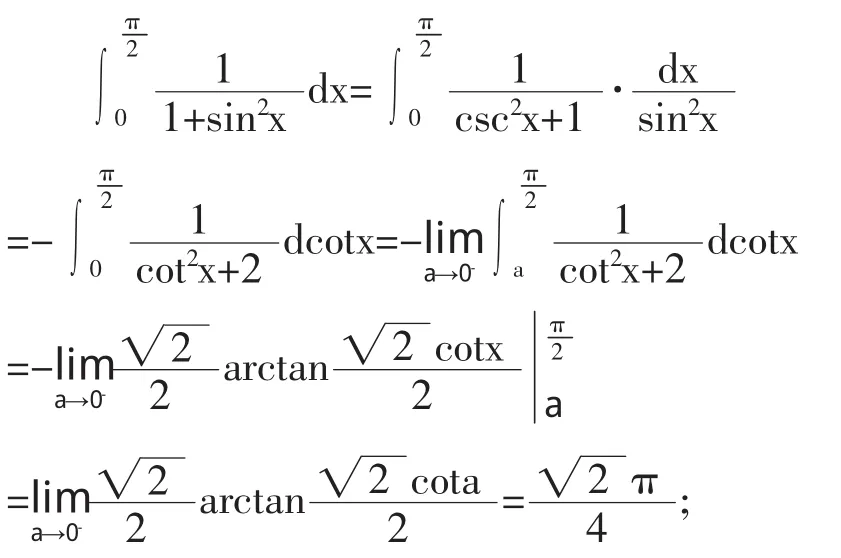
当x≠π时,有
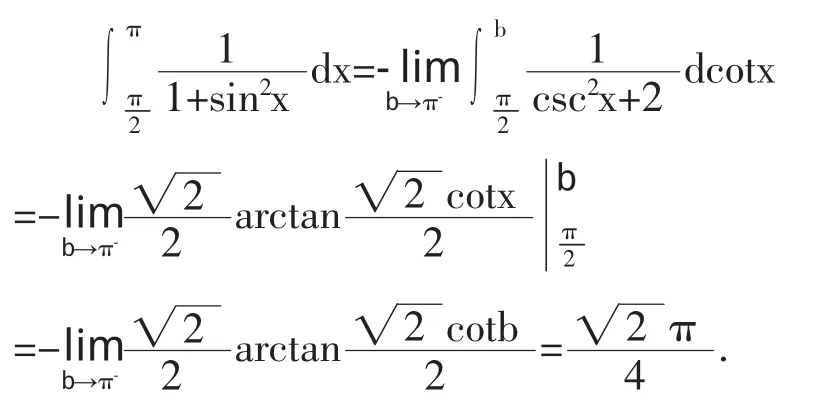
所以,当 x≠0且 x≠π 时,有
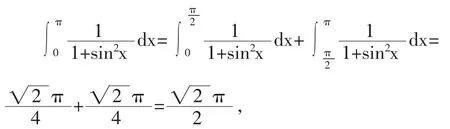
而当x=0与x=π时,都有
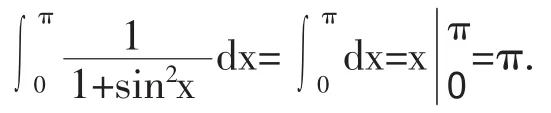
所以,原积分为
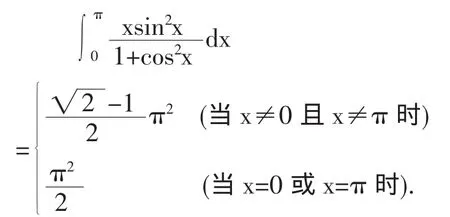
例3和例4都是把一个定积分问题转化成了广义积分问题来解决。
[1]华东师范大学数学系.高等数学[M].华东师范大学出版社,1998.8.
[2]任建娅,司志本,成福伟.高等数学简明教程[M].大连理工大学出版社,2010.8.
