改进的模糊综合评价法在太湖水质类别判定中的应用

鄢 回，郁建桥，徐 洁，陈启美

(1.南京大学电子科学与工程学院，江苏 南京 210093;2.江苏省环境监测中心，江苏 南京210036;3.江苏省环境信息中心，江苏 南京 210036)

·解析评价·

改进的模糊综合评价法在太湖水质类别判定中的应用

鄢 回1，郁建桥2，徐 洁3，陈启美1

(1.南京大学电子科学与工程学院，江苏 南京 210093;2.江苏省环境监测中心，江苏 南京210036;3.江苏省环境信息中心，江苏 南京 210036)

水质判别是一个多参数多级别的模糊概念，基础的模糊综合评价法存在局限性，对基础模糊数学法中隶属度函数及最大隶属度原则进行改进，建立一种改进的模糊综合评价法。以太湖流域水质判别为实例验证了此方法比传统的方法更有效，且适合在太湖流域应用。

水质判别;改进的模糊数学模型;指数隶属度函数;加权评价原则;太湖

水质判别作为一种属性的认知过程，对于水资源开发和利用是十分重要的，并且水质判别的方法在现代环境科学基础理论研究中也是一个重要研究方向。水质判别是一个多指数多级别的模糊概念，模糊综合评价法近年已经广泛地应用于水质判别领域，该方法能有效解决边界模糊问题以及减少监测误差对于判别结果的影响［1，2］。但模糊综合评价法在应用于水质判别时仍存在局限性，例如在强调极值行为时丢失了更多信息，并且采用最大隶属度原则进行水质判别时有明显的信息丢失，可能导致结果的偏差甚至判断错误［3，4］。

为了有效解决这些问题，利用指数隶属度函数以及加权平均原则对原始的基于模糊数学的水质判别法进行改进，建立一种改进的模糊综合评价方法。因指数隶属度函数中每个指标对应不同级别的非零权重值是唯一的，所以可以解决零权重的问题。加权平均原则可以最大化保留评估系数集信息，所以信息丢失的现象可以得到很大的改进，评估结果将会更为合理可信。

太湖地处长江三角洲南缘，是中国第三大淡水湖，水域面积2 338 km2，南北长68.5 km，东西平均宽34 km，湖岸线总长405 km。太湖自西向东在无锡、苏州地区依次分布有竺山湖、梅梁湖、贡湖、漫山湖、胥湖及东太湖等湖湾。太湖是一座天然的平原调蓄水库，具有蓄洪、供水、灌溉、航运、旅游等多种功能［5，6］。太湖又是流域内最重要供水水源地，不仅担负着无锡、苏州和湖州等大中城市的城乡供水，还具有向上海市等下游地区供水并改善水质的作用［7］。20世纪70年代以前，太湖平均水质为Ⅱ类;自80年代起，由于工农业废水和生活污水排放量逐年增加，太湖水质平均每10年下降一个等级，且恶化趋势越来越快，80年代水质为Ⅱ类至Ⅲ类;到90年代，太湖水质继续下降，特别是西北部五里湖、梅梁湖、竺山湖等湖湾，水质基本劣于Ⅴ类;20世纪90年代末以来，太湖水质恶化趋势得到初步遏制，DO、NH3-N、CODMn等主要指标均有所好转，但北部湖湾水质仍为Ⅴ类至劣Ⅴ类。因此亟待提出适合太湖水质判别的方法，用于对太湖水质进行判别，从而更好地进行水质预测、防止水质恶化［8］。改进的模糊综合评价方法适用于太湖水质判别，并且通过实验表明比传统水质判别方法更为有效。

1 基础的模糊综合评价法

模糊综合评价法是一种运用模糊集理论进行客观评价的过程，根据权重综合考虑多个相关指标的贡献，通过使用隶属度函数减少其模糊性。通常i=1，2，…，n，代表评估对象集;j=1，2，…，m，代表评估指标集;k=1，2，…，c，代表评估标准集。模糊综合评价过程如下。

(1)选择评估元素

选择有代表性、合理、准确的评估参数，形成矩阵U，这种选择基于当地实际情况。

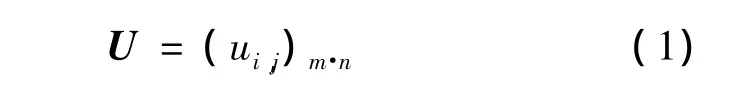
式中:ui，j——第 i个评估对象，第 j个指标的实测值。

(2)建立评估标准集

式中:vj，k——j指标 k 级标准的值。

(3)建立隶属度函数

隶属度函数代表特定浓度隶属于某模糊集的程度。某评估元素对于每一级标准的隶属度可通过以下公式定量计算:

(4)计算权重矩阵

权重是用来反映每个指标污染度的相对比重，权重值计算如式(6)和式(7):

(5)计算评估系数集

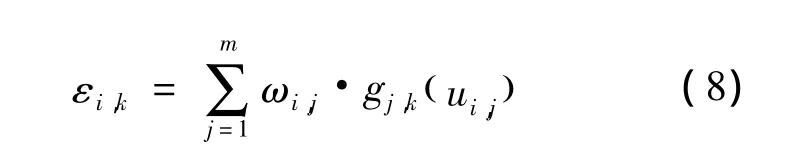
式中:εi，k——评估对象 i对 k 级标准的评估系数。

(6)判别对象级别

采用最大隶属度原则，对象级别是评估系数最大值所对应的级别。

2 改进的模糊综合评价法

2.1 采用指数隶属函数

当计算实际权重，模糊综合评价法总是忽略不相邻级别间的影响，这意味着也许会出现零权重的问题导致扭曲的结果。所以，指数隶属法得以提出:

式中:p——衰减指标，它的值决定了隶属关联度的衰减速率。

采用指数隶属度函数，每个指标对应不同级别的非零权重值是唯一的，所以可以解决零权重的问题。

2.2 采用加权平均原则

最大隶属度原则是一种广泛运用于决策和评估的分析方法。无论如何这种原则有明显的信息丢失缺陷，可能导致判断的失败和结果的偏差。为了避免这一点，提出加权平均原则来代替最大隶属度原则。

使用加权平均原则，提出级别 Z=(Z1，Z2，…，Zc)，如同Z=(1，2，…，c)对于变量，评估系数εi，k用来计算权重，公式如下:

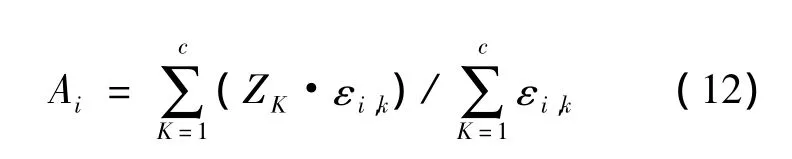
式中:Ai——第i个评估对象的级别特征值。

加权平均原则尽可能多地保留评估系数集信息以避免信息丢失，评估结果将会更合理可信。

3 太湖实例应用及结果分析

国家标准地面水环境质量标准(GB 3838—2002)用于建立太湖水质评估标准集。测试数据来自于2010年6—8月太湖无锡站梅梁湖古竹桥、沙渚、直湖港、马山水厂4个监测站点的实测数据。DO、CODMn、NH3－N被选作评估参数。水质等级被划分为Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类、Ⅴ类等5个级别。当采用改进的模糊综合评价法进行水质评价时，首先建立实测数据集如表1，其次建立评估标准集如表2，再次计算隶属度函数以及计算每个评估参数对应的权重，最后计算评估系数，决定水质级别。

第一组选取了2010年6月—8月太湖无锡站梅梁湖马山水厂监测站点的31组实测数据进行微观水质判别分析，采用加权平均原则计算出的评估系数结果用表3呈现，与此同时采用单因子法、BP神经网络法、原始模糊数学模型的评估结果用表4呈现［9］。另外用Matlab处理得到图1对单因子法、原始模糊数学模型、改进的模糊数学模型的水质评价结果进行了直观显示。

第二组选取了2010年6月—8月太湖无锡站梅梁湖沙渚、直湖港、马山水厂3个监测站点的所有实测数据进行宏观水质趋势分析，采用改进的模糊综合评价法、单因子法、原始模糊数学模型3种方法计算出的评估结果用Matlab编程处理出的图2、图3、图4进行呈现。

对比改进的模糊数学模型的太湖水质评价结果和其他3种方法的水质评价结果可清楚地表明，单因子法由于过度依赖于某单个因子的污染程度，导致其评价结果过高于实际水质情况，从而存在不合理性，表4中单因子法的太湖水质评价结果明显高于改进的模糊数学模型的太湖水质评价结果。改进的模糊数学模型的太湖水质评价结果在31个样本中有25个评价结果与原始的模糊数学模型评价结果相同，相似度高达80%，而不同的6个样本中，例如2010年7月22日6:00的数据，改进的模糊数学模型的太湖水质评价结果为Ⅱ类，而原始模糊数学模型的评价结果为Ⅲ类，产生这种结果的原因是原始模糊数学模型中某单个指标如该样本中的DO浓度(5.28 mg/L)超过该指标Ⅲ类标准。而改进的模糊数学模型通过指数隶属度函数和加权平均原则不仅最大限度保留了某单个指标的水质判别信息，而且更多地考虑了所有指标的影响，因此可以削弱某个因子的值不正常变化所带来的坏的评价影响。所以改进的模糊数学模型比原始的模糊数学模型更为精确有效。另外，从表4中可以看出，改进的模糊数学模型的太湖水质评价结果在31个样本中有29个和BP神经网络方法的评价结果相同，相似度高达93.5%。但是BP神经网络法需要大量的训练样本且效率不高，相比而言改进的模糊数学模型更具有实用性。

从图1、图2、图3、图4可以看出，单因子评价法和原始的模糊数学模型的水质判别结果具有较高的离散性及判别误差，从宏观上很难分析出2010年6—8月太湖无锡站梅梁湖沙渚、直湖港、马山水厂3个监测站点的水质变化趋势，不利于进行水质预测、防止水质恶化。相比而言，改进的模糊数学模型在进行太湖水质判别的过程中，离散度低，且能够很好地表征太湖地区水质变化趋势，有利于水质预测、防止水质恶化。

表1 2010年6月—8月太湖无锡站梅梁湖马山水厂监测站点的31组实测数据 mg/L

表2 国家标准地面水环境质量标准(GB 3838—2002)mg/L

表3 改进的模糊数学模型计算出的评估系数结果

表4 4种方法的水质评估结果

续表4

单因子法、原始模糊数学模型、改进的模糊数学模型的水质评价结果直观显示，绿色点为单因子法评价结果、蓝色点为原始模糊数学模型评价结果、红色点为改进的模糊数学模型评价结果。

绿色点为单因子法评价结果、蓝色点为原始模糊数学模型评价结果、红色点为改进的模糊数学模型评价结果。

绿色点为单因子法评价结果、蓝色点为原始模糊数学模型评价结果、红色点为改进的模糊数学模型评价结果。

绿色点为单因子法评价结果，蓝色点为原始模糊数学模型评价结果，红色点为改进的模糊数学模型评价结果。

4 结论

采用指数隶属度函数以及加权平均原则对原始模糊数学法进行改进，建立一种改进的模糊综合评价方法。在这种新的水质判别方法中，采用指数隶属度函数，解决零权重的问题。加权平均原则用于替代常用的最大隶属度原则，可以尽可能多地保留地评估系数集信息，信息丢失的现象可以得到很大改善。通过对太湖地区实测数据所得结果进行论证对比，改进的模糊数学模型无论是从微观上的水质判别结果精确性和实用性方面还是宏观上的水质趋势的预测能力都远比单因子法、BP神经网络法、原始模糊数学模型更适用于太湖地区水质判别。

［1］GULEDA O E，IBRAHIM D，HALIL H.Assessment of urban air quality in Istanbul using fuzzy synthetic evaluation［J］.Atmospheric Environment，2004，38(23):3809-3815.

［2］WANG H Y.Assessment and prediction of overall environmental quality of Zhuzhou City，Hunan Province，China［J］.Journal of Environmental Management，2002，66(3):329-340.

［3］ICAGA Y.Fuzzy evaluation of water quality classification［J］.Ecological Indicators，2007(7):710-718.

［4］KUNG H，YING L，LIU Y C.A complementary tool to water quality index:Fuzzy clustering analysi［J］.Water Resources Bull，1992，28(3):525-533.

［5］王同生.太湖流域防洪与水资源管理［M］.北京:中国水利水电出版社，2006:10-11.

［6］徐恒省，翁建中，李继影，等.太湖蓝藻水华预警监测与风速风向的关系研究［J］.环境监控与预警，2009，1(2):5-7.

［7］吴浩云.太湖流域“引江济太”水资源调度配置对维护流域河湖健康的思考［C］//房玲娣.水资源管理创新理论与实践.北京:中国水利水电出版社，2006:341-342.

［8］黄漪平.太湖水环境及其污染控制［M］.北京:科学出版社，2001:71.

［9］LU R S，LO S L.Diagnosing reservoir water quality using selforganizing maps and fuzzy theory［J］.Water Research，2002，36(9):2265-2274.

Application of Improved Fuzzy Comprehensive Evaluation Method for Water Quality Assessment in Taihu Lake，China

YAN Hui1，YU Jian-qiao2，XU Jie2，CHEN Qi-mei1
(1.School of Electronic Science and Engineering，Nanjing University，Nanjing，Jiangsu 210093，China;2.Jiangsu Provincial Environmental Monitoring Center，Nanjing，Jiangsu 210036，China;3.Jiangsu Provincial Environmental Information Center，Nanjing，Jiangsu 210036，China)

Considering that the water quality assessment is a fuzzy concept with multiple indicators and classes，and there are still some limits of fundamental fuzzy comprehensive evaluation method，the exponential membership function and the weighted average principle are combined to establish an improved fuzzy comprehensive evaluation method for water quality assessment.The water quality of Taihu Lake is taken as an example and the results showed that the improved fuzzy comprehensive evaluation method is superior to the traditional model and suitable for the application around the Taihu Lake Basin.

water quality assessment;improved fuzzy mathematical model;exponential membership function;weight average principle;Taihu Lake

X824

B

1674-6732(2012)-02-0039-06

10.3969/j.issn.1674-6732.2012.02.010

2011-09-26;

2011-10-25

江苏省环保厅科研项目(2009017);江苏省环境监测科研基金项目(0917);国家水体污染控制与治理科技重大专项项目(2009ZX07528-005-02)。

鄢回(1987—)，在读硕士研究生，从事数据挖掘与环境信息化及其应用研究。