三维社区建模与分析的共形几何代数方法

罗 文，袁 林 旺，胡 勇，易 琳，闾 国 年

三维社区建模与分析的共形几何代数方法

罗 文，袁 林 旺＊，胡 勇，易 琳，闾 国 年

（南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046）

利用共形几何代数的多维统一表达与分析优势，研究了集成多源数据的三维社区统一建模与分析方法。构建了基于多重向量存储结构的社区场景整体建模流程，实现了City GML、DXF等多源数据的导入与集成，并设计了基于共形几何代数的对象运动表达与插值方法。以德国Waldbruecke村为例的验证结果显示，基于共形几何代数的三维社区建模可以较好地表达复杂社区对象，并可以有效支撑几何度量、动态对象跟踪、运动轨迹重建等功能实现。

三维社区;共形几何代数;对象建模;动态分析

城市三维建模与可视化、数字城市建设是城市信息化的重要发展趋势，三维社区建设是其中的重要内容［1，2］。三维社区分析涉及领域的宽泛性决定了其数据的多源性，三维社区建模中常用的数据包含工程测量中的AutoCAD/DXF数据、交通测绘的shapefile数据、数字城市的City GML数据等。如何有效融合多源异构数据，构建多维统一的数据模型成为三维社区建设的难点和重点［3］;另一方面，成熟的三维社区建设不仅要求实现社区建筑、道路网络等多种不同维度、不同类型的实体对象的建模与表达，更需要构建适用于复杂地理场景中多维对象分析的各类分析算法。共形几何代数（Conformal Geometric Algebra，CGA）具有优越的多维表达与分析能力，前期研究表明CGA在GIS对象表达、关系计算及动态场景分析等方面具有优势［4，5］。本文以德国Waldbruecke村的社区规划平面图数据、社区三维建筑物模型数据、道路网络数据等基础地理信息数据为基础，从多源数据整合与集成、场景构建与建模、数据结构设计、系统构建与应用分析等视角入手，探讨基于几何代数的三维社区建模与分析的思路与方法，对三维社区中各类建筑物与运动对象进行建模、表达与分析，尝试为三维社区虚拟仿真、动态表达和空间分析研究提供参考。

1 三维社区场景建模

1.1 Grassmann结构一致的几何形体表达

共形几何代数（CGA）是李洪波等［6］结合共形模型和几何代数的主要优势，对几何代数、射影几何进行拓展后建立的。定义由欧氏空间向共形几何代数空间Cn⊂的变换C（x）为：

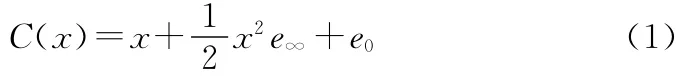
其中：e0和e∞为额外添加的维度支撑向量，分别表示原点和无穷远点。

共形几何代数赋予几何代数空间闵氏内积结构，使得五维向量空间的Grassmann分级结构（C3⊂）完全对应于几何体的分级结构，通过e∞的引入，消除无穷远点的奇异性，统一了线段和圆以及平面和球的表达;同时使得内积可以直接对应于两点间欧氏距离的表征，赋予了内积明确的几何意义。

图1列出了三维空间中常见几何形体的CGA表达，其Grassmann结构一致性直观表现在形体表达形式与几何体维度相一致。表达形式的一致性为几何形体的多维统一建模奠定了基础，也是构建三维社区场景中对象无关、维度无关分析功能的基本前提。

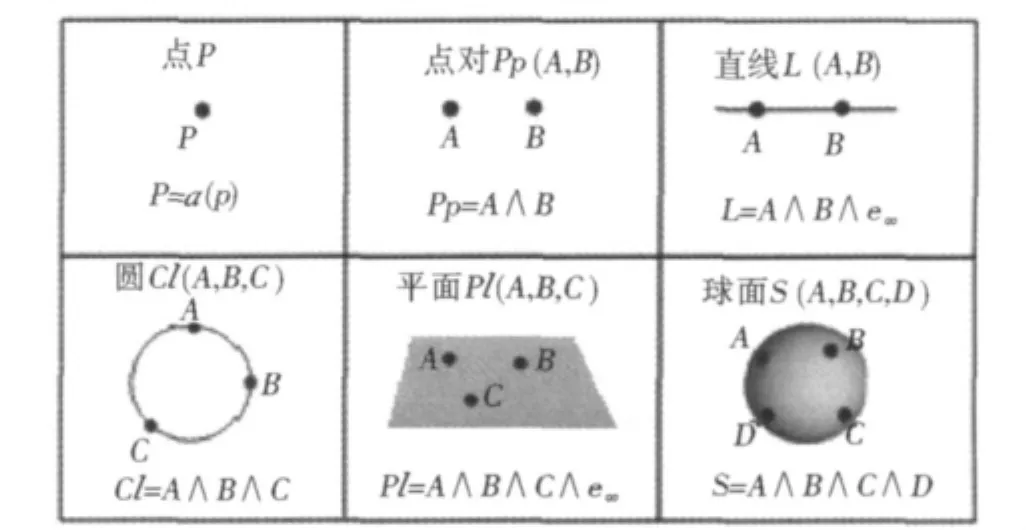
图1 Grassmann结构一致的几何形体表达Fig.1 Geometric representation with consistent Grassmann structure

1.2 基本数据结构设计

基本几何形体数据结构设计如图2所示，鉴于CGA中基本几何形体表达形式具有一致性，可以先设计几何形体基类CGA＿Geo，声明一个32长度的浮点型数组成员变量m＿c用于存储各维度blade系数（blade的概念参见文献［4］），m＿gu用于存储当前对象的维度。在CGA＿Geo的基础上分别派生出点对象（CCA＿Point）、点对＼线段对象（CCA＿Pt Pair）、直线对象（CCA＿Line）、圆对象（CCA＿Circle）、平面对象（CCA＿Plane）和球面对象（CCA＿Sphere），并针对各对象特点分别定义其特有的属性和方法。

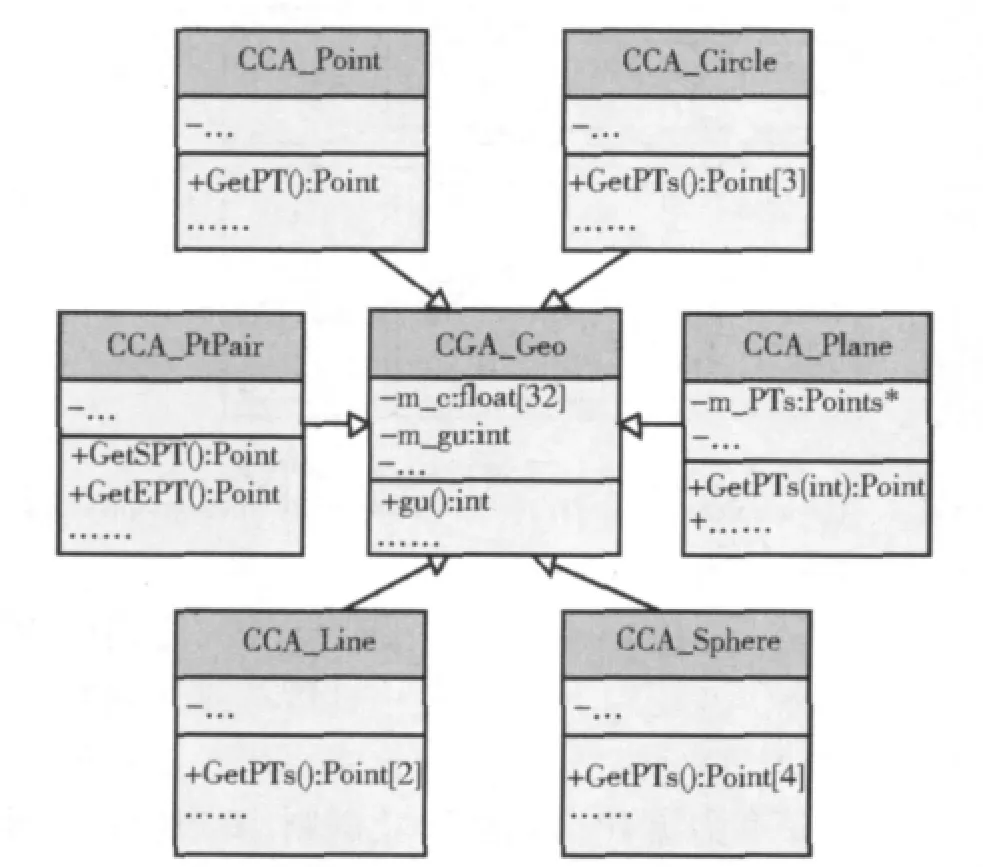
图2 基本几何形体的数据结构Fig.2 Data structure of basic geometric objects

CGA＿Geo类的另一重要作用在于：当几何体未知时可以先将其声明成CGA＿Geo类型，经过运算后，通过提取grade运算判断其维度，进而分析得到其具体类型。当形体已知时，声明其对应类型，可有效提升存储空间效率和运算时间效率。基于上述特性，在分析功能设计中，可将任意几何体当做CGA＿Geo类参与运算，从而实现对象无关的表达与运算。

1.3 三维社区建模与组织

三维社区场景建模要求实现三维场景中基本几何对象几何、拓扑关系的重建及语义关系的嵌入。同维度几何对象可通过关系表、链表等结构简单连接，但不同维度对象统一建模与表达则是几何、拓扑建模的难点所在。多重向量（multivector）是几何代数中与blade相对应的一个概念，multivector通过“＋”连接不同维度的blade，实现混合维度对象的存储，且在几何代数理论体系中已经形成一套相对完备的针对multivector的分析方法［7］。据此，可以将基本几何形体用“＋”连接成如下形式：

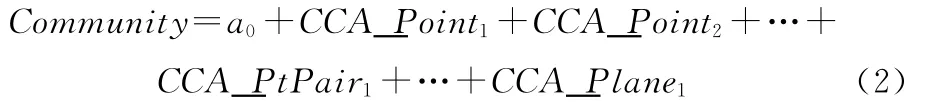
式（2）同时包含了点、线段和面对象，其连接顺序采用基于对象类别的分类排列方法，式中“＋”仅用于表达关系计算，而不进行数值上的累加与归并。语义关系的嵌入则以关系表为基础，通过ID与几何对象相链接。

1.4 多源数据集成框架

基于上述场景建模思路构建空间数据解析流程（图3）。首先应用数据解析器得到几何数据和属性数据，判断几何数据类别，分别将其存储为对应的结构，然后根据数据本身的层次结构生成相应的多重向量的统一存储。以地理对象为单位对多重向量进行ID标识，并将其与存入属性表中的属性数据相关联。以CityGML数据和AutoCAD的DXF交换格式两种主要数据类型的解析与集成方法为例，进行基于几何代数的三维社区建模示范。

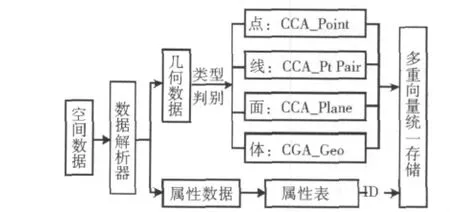
图3 空间数据解析流程Fig.3 Parsing flow of spatial data

CityGML数据以XML文本标识语言为基础，以树型结构存储其几何拓扑信息［8］。通过其最顶层的数据根节点City ObjectsRoots管理场景，以下依次为City Object、Geometry、面、线、点，每个节点都有与之对应的属性信息，包含用于区分对象类型（屋顶、墙壁等）的数据标签以及用于可视化渲染的颜色和材质信息。City GML数据的解析与集成类似于树的中序遍历，即先读取当前节点，再读取其各个组成部分，从而实现拓扑关系的重建。结合分析需要，将数据按一定的粒度进行对象划分，并为其分配唯一的ID进行标识，连接属性信息。

DXF数据是AutoCAD的绘图交换文件，是由很多的“代码”和“值”组成的“数据对”构造而成［9］。这些“代码”包含对DXF文件头、块、图层及实体对象等的定义。DXF数据的解析过程与CityGML基本类似，但需进行数据中块的处理。此外，由于DXF数据本身不具备严密的拓扑信息，所以前期需要对数据的拓扑加以修正。

2 对象运动表达与插值

2.1 基本几何分析

共形几何代数的闵氏内积结构使得内积运算具有表达对象距离的几何意义，进而实现了内蕴距离、方向等几何关系的共形几何代数表达。如对于两个给定点p、q，其距离计算公式为：p、q分别为经共形转换后点的表达。而直线间的角度则可根据二者所在向量内积与向量模的比值确定。

2.2 对象运动表达

CGA中平移、旋转和缩放等欧氏变换可统一于同一变换框架下［10］。基于CGA的运动表达的一般形式为：Or＝RoR′，其中o为运动对象，R为运动的统一表达，也称作versor表达。对于任意的versor表达，很难直观地获得其确切的几何意义，但奇次阶的versor则可通过其指数形式揭示其内蕴的几何意义。如指数形式表达的变换R＝e－φl/2表示以l为旋转轴、旋转角度为φ的rotor，其证明过程如下：

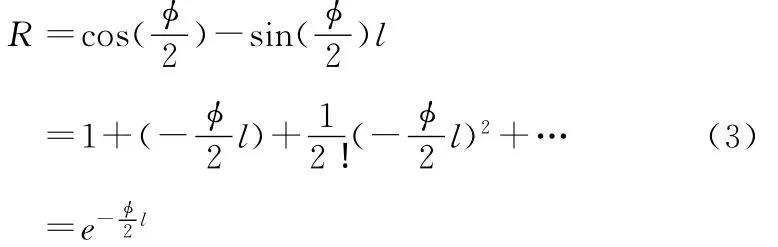
2.3 对象运动插值

基于指数形式的versor表达可通过对数变换将其线性化，从而获得相关运动参数，进行运动轨迹重构及线性运动平滑插值。任意欧氏空间的刚体运动与变换均可通过共形空间中的versor精确表达［11］。由于任意奇次阶versor均可表达为bi-vector的指数形式，即：V＝eB，对该式两边分别取对数可得：B＝ln（V），且任意bi-vector均为线性结构，因此基于指数形式表达的versor可以直接进行诸如平均、插值、外推等数值运算。如基于rotor指数形式表达，其插值公式为：

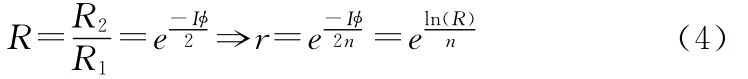
式（4）实现了将R1到R2的运动插值为n次的运动r。基于上述算子可实现欧氏空间中复杂运动的表达与分析。由于基于几何代数的旋转表达算子的符号直接表征了其运动方向［12］，类似地可从基于几何代数的运动表达中解析出运动内在的特性信息。

3 系统实现与验证

3.1 系统架构

设计基于共形几何代数的三维社区集成构建系统对上述思路加以验证，系统层次架构如图4所示。数据资源层包括CityGML、DXF和Shape等常用的空间数据，数据组织层为前述多源数据集成方法及基于CGA的多维统一存储，设计场景动态监控与运动对象插值的功能分析层，最后是基于VTK渲染的场景可视化与场景交互的表现层。该系统以共形几何代数为理论支持，多维统一建模为主线，场景动态分析为最终目标，实现面向多源数据的三维社区场景建模与分析。

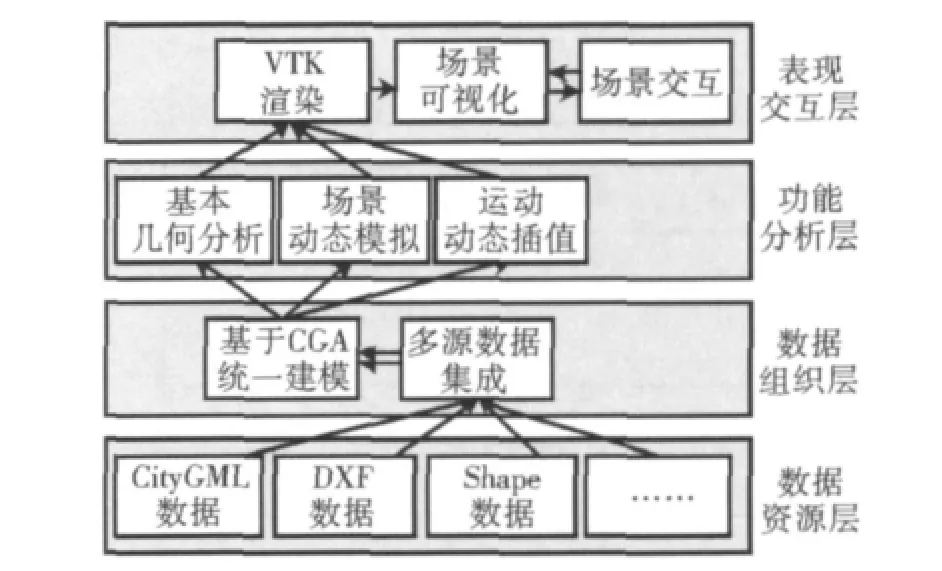
图4 三维社区集成构建系统架构Fig.4 The architecture of 3D resident community integration system

3.2 案例数据

以德国Waldbruecke村为研究样区，使用的主要数据及格式如表1所示。其中社区三维建筑物的模型数据与数字化的道路网数据主要用于场景的构建，车辆模型数据和车辆位置数据则用于场景动态模拟及场景内动态对象的插值分析。

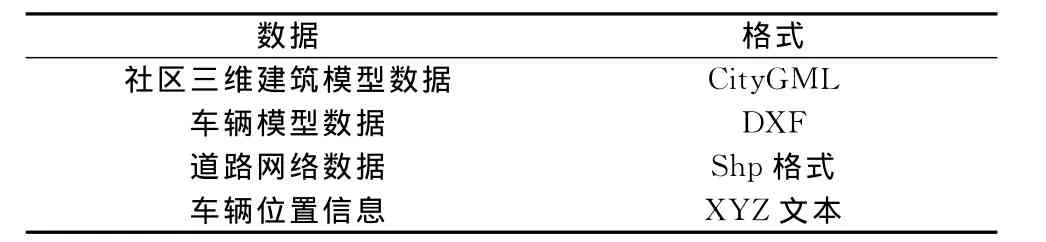
表1 主要数据及其格式Table 1 The main data and its format

3.3 三维建模与分析

首先对City GML场景数据、DXF车辆数据和Shape格式的道路数据集成建模，建模结果可通过系统可视化模块进行渲染可视化（图5a）。在基于几何代数的三维社区建模中，由于不同维度几何对象均处于同一场景，可对其集中管理。图5b演示了场景中对三维建筑对象的交互式选取与可视化功能。基于CGA框架的三维场景建模可实现场景中对象几何关系的批量计算及运动对象动态插值。应用车辆模型和车辆位置模拟数据，可对车辆在场景中的运动情况进行动态模拟，并实时计算其距离与角度等基本几何关系（图5c），图中雷达图与箭头图分别显示的是车与选中建筑的距离和角度。图5d为运动对象插值计算演示，图中黑色轨迹为读取的原始数据，灰色轨迹为经过versor插值后的样点数据，由结果可知，基于versor的运动插值可保证插值轨迹相对均匀、平滑，且可推算出任意时刻车辆所在的位置信息及其运动参数。

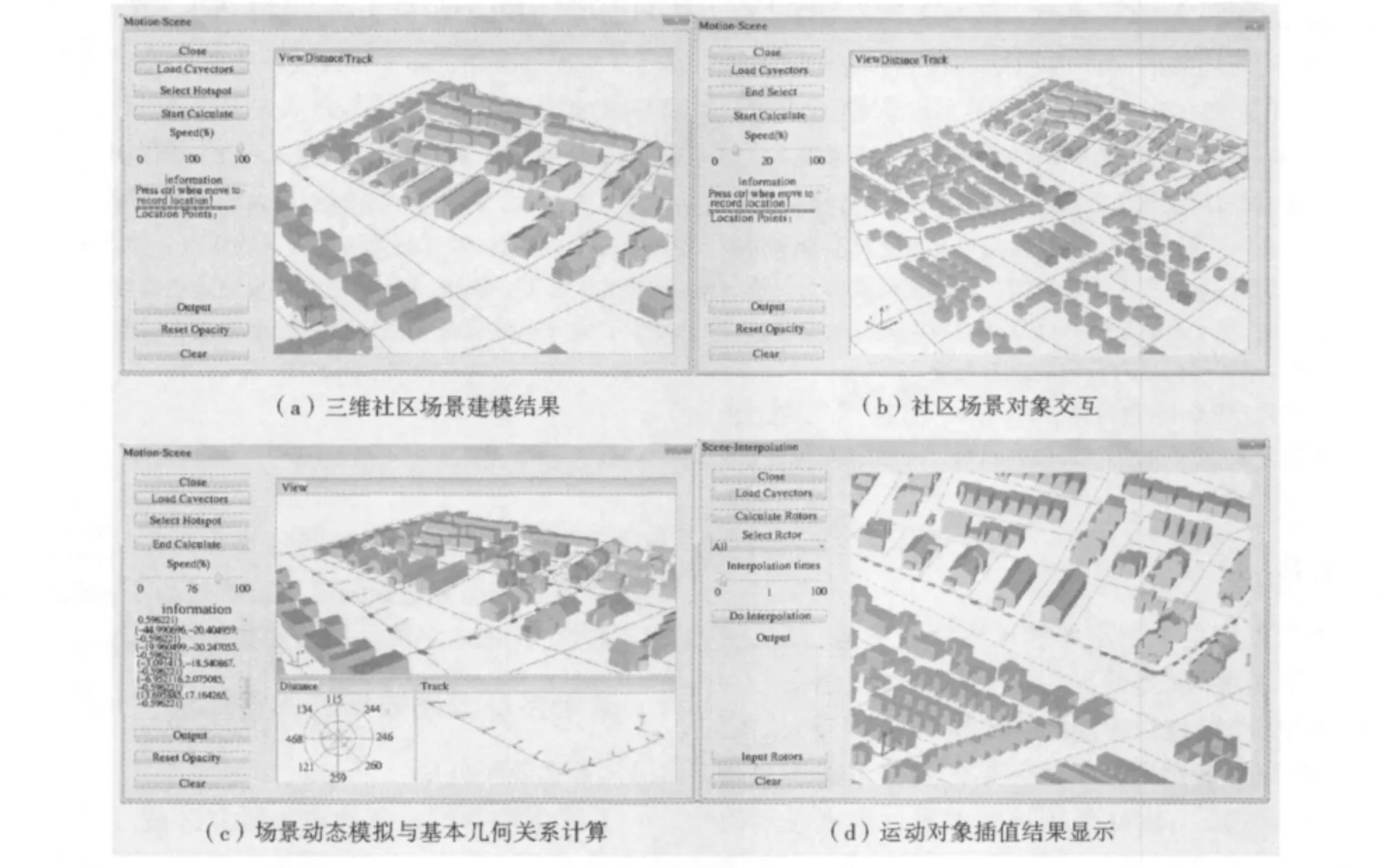
图5 三维社区对象建模与运动分析Fig.5 Modeling and motion analysis of 3D resident community

4 结论与讨论

本文以CGA为基础，设计了基于多重向量的三维社区统一存储模型，利用其在多维对象建模与分析上的优势，构造了可支撑多源数据集成的三维社区建模与分析的整体流程。利用几何代数算子与基于versor的运动表达，构造了包括几何度量、动态对象运动表达及运动插值等场景对象动态表达和分析方法。对德国Waldbruecke村三维社区的实例分析显示，本文提出的三维社区建模与分析方法可以很好地支撑复杂三维社区场景对象的表达与建模，并可有效支撑三维社区中运动对象的模拟与分析，从而为三维社区建设提供良好的理论支撑与开发工具。

几何代数优越空间构造能力与多维对象统一表达机制可以有效支撑三维场景中复杂对象的表达与分析，基于几何代数的动态对象表达与分析不仅可以再现对象动态运动与演化的轨迹与过程，实现对象运动过程的直观再现，更可以有效保持原有运动轨迹的运动参数特征，从而直接支撑复杂的时空及运动分析。以几何代数为基础，对现有三维社区分析方法及更广泛的地理分析模型进行重建与集成，有望提升现有三维社区GIS的建模、表达与分析能力，为其向时态GIS方向的发展及更广泛的领域应用提供数据建模、计算方法以及分析模型支撑。

［1］田宜平，李伟忠，何珍文.数字城市中三维数字社区的解决方案［J］.计算机工程与应用，2004，40（1）：223－226.

［2］孙敏，马蔼乃，陈军.三维城市模型的研究现状评述［J］.遥感学报，2002，6（2）：155－161.

［3］宋关福，钟耳顺，刘纪远，等.多源空间数据无缝集成研究［J］.地理科学进展，2000，19（2）：110－115.

［4］YUAN L W，YU Z Y，CHEN S F，et al.CAUSTA：Clifford algebra based unified spatio-temporal analysis［J］.Transactions in GIS，2010，14（s1）：59－83.

［5］袁林旺，俞肇元，罗文，等.基于共形几何代数的GIS三维空间数据模型［J］.中国科学（D辑），2010，40（12）：1450－1461.

［6］李洪波.共形几何代数——几何代数的新理论和计算框架［J］.计算机辅助设计与图形学学报，2005，17（11）：2383－2393.

［7］PERWASS C.Geometric Algebra with Applications in Engineering［M］.Heidelberg：Springer-Verlag，2009.

［8］巫兆聪，欧阳群东，李芳芳.基于City GML的遥感信息共享研究［J］.武汉大学学报（信息科学版），2010，35（4）：423－426.

［9］孙晓莉，赵俊三.DXF文件到Shape文件无损转换方法的研究［J］.科学技术与工程，2011，11（14）：3336－3341.

［10］刑燕，檀结实.图形变换和运动的共形几何代数表示方法［J］.计算机应用研究，2008，25（9）：2842－2844.

［11］DORST L，FONTIJNE D，MANN S.Geometric algebra for computer science［A］.The Morgan Kaufmann Series in Computer Graphics［C］.Morgan Kaufmann Elsevier，2007.

［12］李洪波.共形几何代数与运动和形状的刻画［J］.计算机辅助设计与图形学学报，2006，18（7）：895－901.

Conformal Geometric Algebra-Based 3D Resident Community Modeling and Analysis

LUO Wen，YUAN Lin－wang，HU Yong，YI Lin，LV Guo－nian
（KeyLaboratoryofVGE，MinistryofEducation，NanjingNormalUniversity，Nanjing210046，China）

Conformal Geometric Algebra（CGA）is a relatively new geometric model for geometric primitives representation，it also offers a language of operations to manipulate those primitives.Based on these advantages，this paper explored the method for multi-source data integration and unified modeling and analysis of the three dimensional resident community.As well as the storage structure founded on multi-vectors，the modeling procedures of the whole community scene were constructed，supporting multi-format data importing and integration such as City GML and DXF.Furthermore，the moving object expression and dynamical interpolation methods were illustrated.The proposed modeling and analysis methods were experimented on the German Waldbruecke village data.The results suggest that the three dimensional resident community modeling based on CGA can effectively express complex community objects，as well as analysis functions e.g.geometric measurements，dynamical objects tracking and motion trajectory reconstruction.

3D resident community;CGA;object modeling;dynamical analysis

P208

A

1672－0504（2012）03－0020－04

2011－10- 30;

2011－12－31

国家自然科学基金“基于几何代数的多维统一空间关系计算模型及并行化方法”（41171300）;国家863资助课题 “基于Clifford代数的时空统一数据模型关键技术研究”（2009AA12Z205）

罗文（1986－），男，博士研究生，主要从事GIS理论与算法研究。＊通讯作者E－mail：yuanlinwang＠njnu.edu.cn