Analysis of Bifurcation and Stability on Solutions of a Lotka-Volterra Ecological System with Cubic Functional Responses and Di ff usion∗
2012-12-27JIAYUNFENGWUJIANHUAANDXUHONGKUN
JIA YUN-FENG,WU JIAN-HUAAND XU HONG-KUN
(1.College of Mathematics and Information Science,Shaanxi Normal University,
Xi’an,710062)
(2.Department of Applied Mathematics,National Sun Yat-sen University, Kaohsiung 80424,Taiwan)
Analysis of Bifurcation and Stability on Solutions of a Lotka-Volterra Ecological System with Cubic Functional Responses and Di ff usion∗
JIA YUN-FENG1,WU JIAN-HUA1AND XU HONG-KUN2
(1.College of Mathematics and Information Science,Shaanxi Normal University,
Xi’an,710062)
(2.Department of Applied Mathematics,National Sun Yat-sen University, Kaohsiung 80424,Taiwan)
This paper deals with a Lotka-Volterra ecological competition system with cubic functional responses and di ff usion.We consider the stability of semitrivial solutions by using spectrum analysis.Taking the growth rate as a bifurcation parameter and using the bifurcation theory,we discuss the existence and stability of the bifurcating solutions which emanate from the semi-trivial solutions.
Lotka-Volterra ecological system,stability,bifurcating solution
1 Introduction
It is one of the elementary concerns of many researchers that analyze the dynamics of biological populations by reaction-di ff usion equations.During the past decades,intensive studies in pursuing the ecological systems with various boundary conditions derived from interacting processes of several species have been investigated mathematically.These systems,such as the Lotka-Volterra models(see[1–7]),Leslie-Gower models(see[8–10]),Sel’kov models (see[11–13])and Brusselator models(see[14–16])are important research branches.In these references,the authors discussed different ecological models with various boundary conditions.They analyzed the dynamical behavior of these models in different ways,including theexistence,nonexistence,boundedness,bifurcation,the stability and some other characters of positive solutions to these models,and many valuable and classical results were obtained.
Among numerous literatures on Lotka-Volterra models,the reaction terms of quadratic are relatively common.In the present paper,we investigate the following Lotka-Volterra competition reaction-di ff usion system with cubic functional responses:

whereΩ⊂RNis an open,bounded domain with smooth boundary∂Ω,u=u(x,t)and v=v(x,t)are the population densities of the two competing species,d1and d2are the di ff usion coefficients of u and v,a and e represent their respective birth rates,b and g account for the self-regulation of each species,and c and f describe the competition between the two species.All the parameters are positive constants.The homogeneous boundary condition means that the habitatΩwhere the two species live is surrounded by a hostile environment. With these interpretations,only solutions of(1.1)with u and v nonnegative are physically of interest.
Biologically,we can interpret this system as follows.The functions a−bu2,fu2,e−gv2and cv2describe how species u and v interact among themselves and with each other.Firstly, the case f>b and c>g means that the species u interacts strongly with species v and weakly among themselves.Similarly,for species v,they interact more strongly with u than they do with themselves.Hence,when f>b and c>g,the equations in(1.1)model a highly competitive system.Secondly,the opposite situation happens when f<b and c<g, namely,both species interact more strong among themselves than they do with the other species.So,when f<b and c<g,the equations in(1.1)model a weakly competitive system.Thirdly,when both f=b and c=g,each species interacts with the other almost at the same rate with that they interact among themselves.If a=e,this can be interpreted as the maximum relative growth rates being the same for both species.
If we only consider the case that u and v are functions of x alone,then it is natural to look for the steady-state solutions of(1.1).Furthermore,if both components of such a solution are strictly positive,it is referred to as a coexistence state.The main aim of this paper is to study the bifurcation and stability of the steady-state solutions of the system (1.1),that is,to study the bifurcation and stability of the classical solutions of the following elliptic system:

The organizationof this paper is as follows.In Section 2,by using the method of spectrum analysis,we first give the stability of the semi-trivial solutions of the system.In Section 3, by the bifurcation theory,we discuss the existence and stability of the bifurcating solutions which emanate from the semi-trivial solutions.Unlike other more conventional literatures, here,taking a different approach,we investigate the stability of the bifurcating solutions by considering the higher derivative of the corresponding function instead of the first derivative, since the first derivative is just equal to zero.We think that in many biologically important cases this technique turns out to be e ff ective for analyzing the stability of the solutions. Moreover,the methods of nonlinear analysis and the tools of nonlinear partial differential equations that we used in the present paper are somewhat useful for different readers in applied subjects.
For the sake of convenience,we first give some preliminaries.
We denote by λ1(q)the principal eigenvalue of the problem
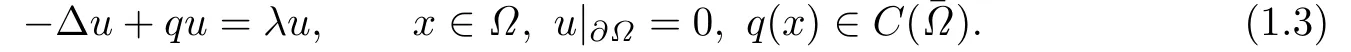
Then λ1(q)is increasing in q.Let λ1(0)=λ1.Then λ1>0(see[17]).
2 Stability of Semi-trivial Solutions
In this section,we analyze the stability of the semi-trivial solutions of the system(1.2).To do this,we first need a lemma.
Lemma 2.1[18]Leth(u)be a strictly decreasing smooth function on[0,∞)withh(u)≤0
foru≥c0for some constantc0.Ifh(0)>λ1,then the boundary problem
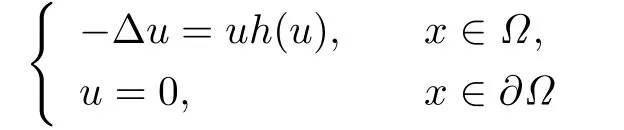
has a unique positive solution.Ifh(0)≤λ1then0is the only non-negative solution.
According to Lemma 2.1,we know that the problems
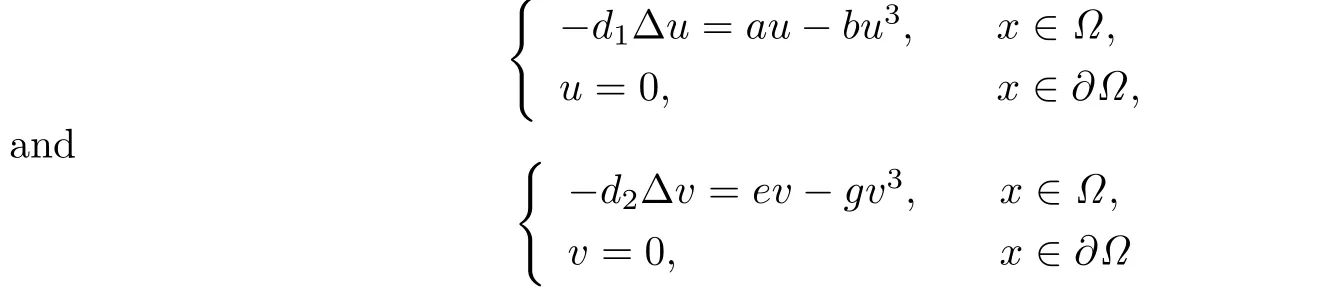
both have a unique positive solution u∗and v∗,respectively,provided that
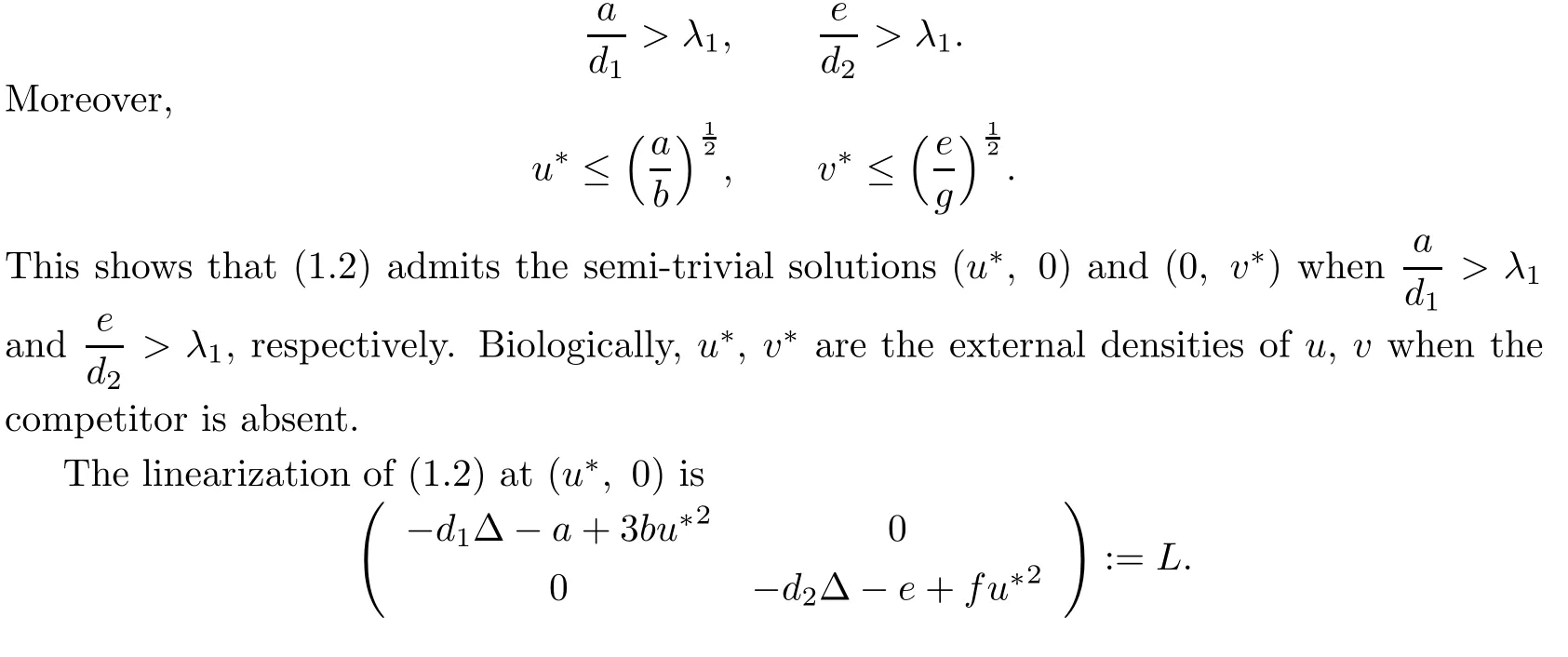
Let

Then it is known that all eigenvalues of L1are positive by the monotonicity of the principal eigenvalue λ1(q)of(1.3).By[19],we know that all eigenvalues of L are σ(L1)∪σ(L2),where σ(L1)and σ(L2)are the spectrum sets of L1and L2,respectively.Thus,we have

3 Existence,Uniqueness and Stability of Bifurcating Solutions Emanating from the Semi-trivial Solutions
In this section,by using the Crandall-Rabinowitz bifurcation theorem,we take e as a parameter to discuss the bifurcating solution of(1.2),which bifurcates from(u∗,0).Theorem 2.1 shows that(u∗,0)is asymptotically stable when λ1(−d2∆+fu∗2)>e.So,in this case, there exists no bifurcating solution emanating from(u∗,0).Therefore,it is necessary to assume that the stable condition in Theorem 2.1 does not hold.
Since the operator−d1∆−a+3bu∗2is positive,whether GU(U∗;e)is degenerate or not is completely determined by−d2∆−e+fu∗2.For this reason,we set
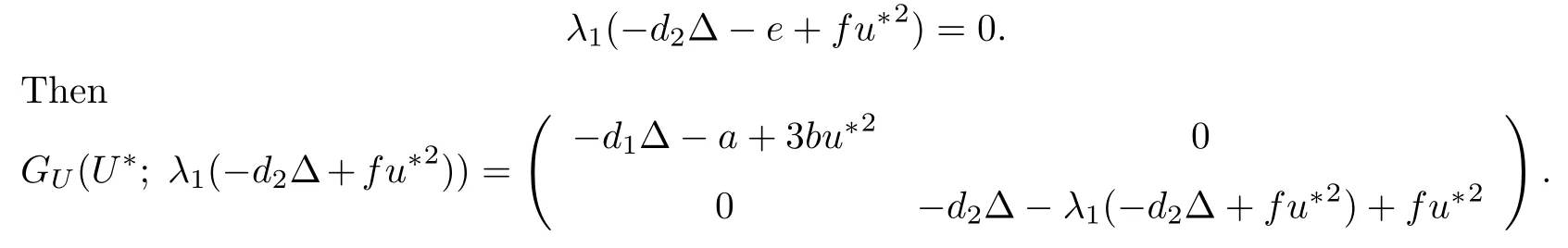
Remark 3.1λ1(−d2∆−e+fu∗2)=0 implies that λ1(−d2∆+fu∗2)must be positive. In fact,this assertion holds.For the eigenvalue problem (

by the variational principle of eigenvalues(see[20]),we know that the principal eigenvalue λ1(−d2∆+fu∗2)is given by
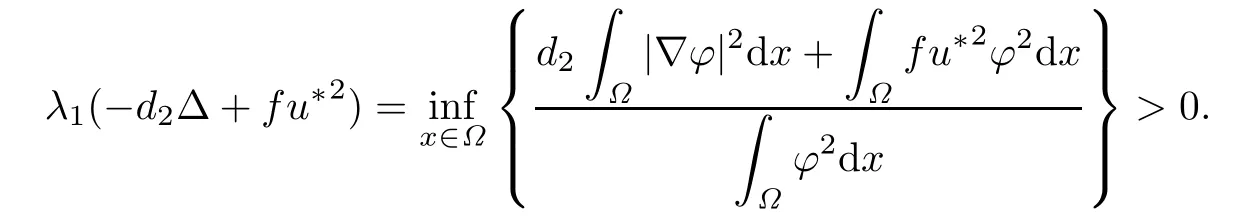
The bifurcation result reads as follows.


So GUe(U∗;λ1(−d2∆+fu∗2))(0,ψ)T/∈R(GU(U∗;λ1(−d2∆+fu∗2))).
Hence,by the Crandall-Rabinowitz bifurcation theorem(see[21]),there exist some s0>0 and sufficiently smooth functions β:(−s0,s0)−→Rand(ω1,ω2)T:(−s0,s0)−→ X satisfying



This shows that mu∗is a lower solution of(3.3).Furthermore,it is obvious that 0 is an upper solution of(3.3).Therefore,we have
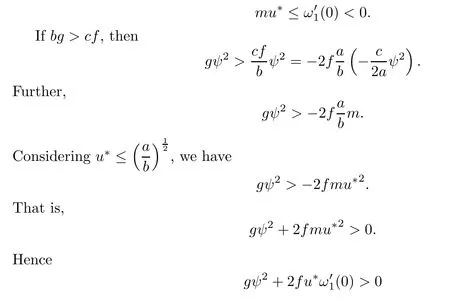
(note that m<0 and ω′1(0)<0).This leads to
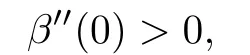
and for s>0,small enough,
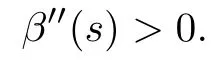
This implies that β′(s)is monotone increasing near s=0.Since β′(0)=0,we know that
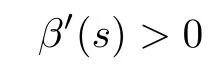

[1]Leung A.Equilibria and stabilities for competing-species,reaction-di ff usion equations with Dirichlet boundary data.J.Math.Anal.Appl.,1980,73:204–218.
[2]Cosner R C,Lazer A C.Stable coexistence state in the Volterra-Lotka competition model with di ff usion.SIAM J.Appl.Math.,1984,44:1112–1132.
[3]Li L,Logan R.Positive solutions to general elliptic competition models,differential Integral Equations,1991,4:817–834.
[4]Wang L,Li K.On positive solutions of the Lotka-Volterra cooperating models with di ff usion.Nonlinear Anal.,2003,53:1115–1125.
[5]Roeger L-I W.A nonstandard discretization method for Lotka-Volterra models that preserves periodic solutions.J.differential Equations Appl.,2005,11:721–733.
[6]Jia Y,Wu J,Nie H.The coexistence states of a predator-prey model with nonmonotonic functional response and di ff usion.Acta Appl.Math.,2009,108:413–428.
[7]Blat J,Brown K J.Global bifurcation of positive solutions in some systems of elliptic equations.SIAM J.Math.Anal.,1986,17:1339–1352.
[8]Aisharawi Z,Rhouma M.Coexistence and extinction in a competitive exclusion Leslie-Gower model with harvesting and stocking.J.differential Equations Appl.,2009,15:1031–1053.
[9]Haque M,Venturino E.E ff ect of parasitic infection in the Leslie-Gower predator-prey model.J.Biol.Systems,2008,16:425–444.
[10]Korobeinikov A.A Lyapunov function for Leslie-Gower prey-predator models.Appl.Math. Lett.,2001,14:697–699.
[11]Davidson F A,Rynne B P.Local and global behaviour of steady-state solutions of the Sel’kov model.IMA J.Appl.Math.,1996,56:145–155.
[12]Wang M.Non-constant positive steady states of the Sel’kov model.J.differential Equations, 2003,190:600–620.
[13]Lieberman G M.Bounds for the steady-state Sel’kov model for arbitrary p in any number of dimensions.SIAM J.Math.Anal.,2005,36:1400–1406.
[14]Kuptsov P V,Kuznetsov S P,Mosekilde E.Particle in the Brusselator model with flow.J. Phys.D,2002,163:80–88.
[15]Kang H,Pesin Y.Dynamics of a discrete Brusselator model:escape to in fi nity and Julia set,Milan J.Math.,2005,73:1–17.
[16]Golovin A A,Matkowsky B J,Volpert V A.Turing pattern formation in the Brusselator model with superdi ff usion.SIAM J.Appl.Math.,2008,69:251–272.
[17]Ye Q,Li Z.Introduction to Reaction-Di ff usion Equations.Beijing:Science Press,1990.
[18]Berestyski H,Lions P L.Some applications of the method of super and subsolutions.Lecture Notes in Math.,1980,782:16–42.
[19]Yamada Y.Stability of steady states for prey-predator di ff usion equations with homogeneous Dirichlet conditions.SIAM J.Math.Anal.,1990,21:327–345.
[20]Keener J P.Principles of Applied Mathematics.MA:Addision-Wesley,Reading,1987.
[21]Crandall M G,Rabinowitz P H.Bifurcation,perturbation of simple eigenvalues and linearized stability.Arch.Rational Mech.Anal.,1973,52:161–181.
[22]Smoller J.Shock Waves and Reaction-Di ff usion Equations.New York:Springer-Verlag,1983.
Communicated by Shi Shao-yun
92D25,93C20,35K57
A
1674-5647(2012)02-0127-10
date:March 17,2008.
This work is supported partly by the NSF(10971124,11001160)of China and NSC(97-2628-M-110-003-MY3)(Taiwan),and the Fundamental Research Funds(GK201002046)for the Central Universities.
杂志排行
Communications in Mathematical Research的其它文章
- The Budget Constrained Multi-product Newsboy Problem with Reactive Production: A Problem from Entrepreneurial Network Construction∗
- Trivariate Polynomial Natural Spline for 3D Scattered Data Hermit Interpolation∗
- Stability of Fredholm Integral Equation of the First Kind in Reproducing Kernel Space∗
- Stability of Global Solution to Boltzmann-Enskog Equationwith External Force∗
- Likely Limit Sets of a Class of p-order Feigenbaum’s Maps∗
- Computing Numerical Singular Points of Plane Algebraic Curves∗
