模糊控制在污水技术评估实验室温控系统中的应用

张伟，许春莲* ，黄海明，马爱君，武少伟

1.中国环境科学研究院，北京 100012

2.山东电子职业技术学院，山东 济南 250200

为适应我国环境保护技术的快速发展，有效提升环境保护能力，开展了水污染防治生物技术实验室验证评估。通过对生物处理新技术全面客观的验证评估，可以有效地进行新技术推广，推动环保技术的创新发展。在实验室验证评估过程中，为满足微生物的生存需要，验证评估用的原水需具有适当和稳定的温度。按照工艺流程，来自居民楼的生活污水首先经格栅处理后与冷冻液进行热交换，变为5℃的实验用原水，然后通过加药进行水质调整，使水质保持在稳定的范围内，进入污水处理设备前需经过与65～80℃热水进行热交换使水温达到13～20℃，以满足验证评估客观性和科学性的要求。

由于温度控制系统具有不确定、非线性、大滞后等特点，常规的PID控制难以满足验证评估所需原水温度控制要求［1］。1964年美国的Zadeh教授创立了模糊集合理论，1974年英国的Mamdani研制出第一台模糊控制器。模糊控制器不需要了解对象的精确数学模型，根据专家知识进行控制，用模糊控制器实现对温度控制系统的控制，大大改进了原系统的控制效果，在一定程度上满足了系统快速性的要求［2-6］。针对生物处理技术实验室验证评估过程中原水升温控制系统，笔者设计了一种自适应模糊控制器，根据温控系统中热交换器后原水温度的反馈，通过模糊规则推理和决策，在线整定控制参数，以实现对验证评估用原水温度的自适应控制。

1 原水温度控制系统

水污染防治生物处理技术实验室验证评估过程中，进入生物技术处理流程的原水应具有合适、稳定的温度。收集于生活区的原水经过低温储存、水质调整，与锅炉提供的热水通过热交换器，水温升至验证所需的温度后，直接进入生物技术处理流程，开始验证评估工作。温度控制系统主要是保证原水出水有恒定的预设温度，控制元件是热水调节三通阀，该阀门控制流经交换器热水的流量，将预设定的原水温度作为给定值，经热交换后原水的温度作为反馈值，阀门的开度作为输出值，以保证流入生物技术处理单元的原水温度的恒定。原水温度控制系统原理如图1所示。

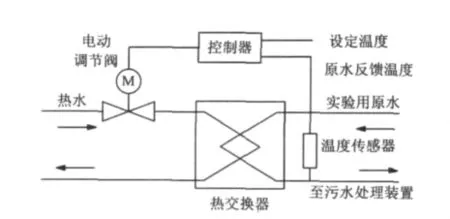
图1 温度控制系统原理Fig.1 The principle diagram of temperature control system

2 模糊控制器设计

由于被控对象的复杂性(非线性)，难以建立精确的数学模型，因此，有关被控对象的知识主要来源于领域专家或操作人员的知识和经验。针对验证评估中的温度控制系统，通过控制原理可以确定基本控制策略。因此设计一种自调整模糊控制器，可实现动态和稳态性能很好的控制。模糊控制器结构如图 2 所示［7-9］。

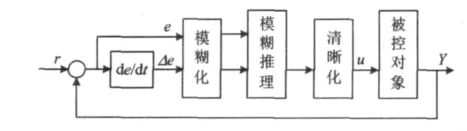
图2 模糊控制器结构Fig.2 The structure diagram of fuzzy controller

在运行中不断地检测偏差和偏差变化率，将其输入模糊控制器进行模糊化，运用模糊推理，进行模糊运算，对输出控制量在线修改并清晰化，作用于被控对象，使被控对象具有良好的静态及动态性能。模糊控制器的设计分为清晰量的模糊化、模糊控制规则和模糊量的清晰化三部分。

2.1 清晰量的模糊化

在模糊控制系统运行中，控制器的输入值、输出值是有确定数值的清晰量，而在进行模糊控制时，模糊推理过程是通过模糊语言变量进行的，因此需将物理量的清晰值转换成模糊语言变量。

该控制器中各语言变量的论域设定如下:

为计算机处理方便且不影响仿真结果，在该控制器中论域E、EC及U等语言变量的隶属函数取三角函数(图3)。

2.2 模糊控制规则

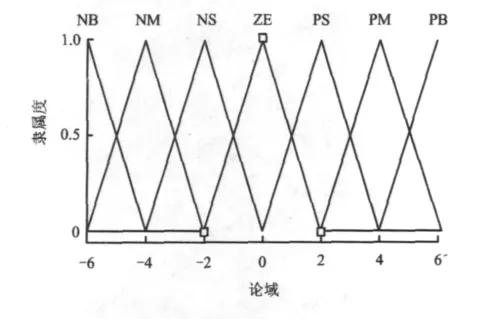
图3 E、EC及U的隶属函数Fig.3 The membership function of E，EC and U

模糊控制规则是基于手动控制策略建立的，而手动控制策略又是人们通过学习、实验以及长期经验积累而逐渐形成的［3］。从系统的稳定性、响应速度、超调量和稳态精度等各方面考虑，根据过程模糊模型生成控制规则。当偏差较大时，对偏差给予较大权重，以尽快消除误差，提高响应速度;当偏差较小时，为避免系统超调，对偏差变化率的影响给予较大的权重，以尽快进入稳态［10-12］，据此生成模糊控制规则，如表1所示［2］。为表明论域E、EC及U之间的控制关系，根据模糊控制规则生成的模糊控制规则表面如图4所示。

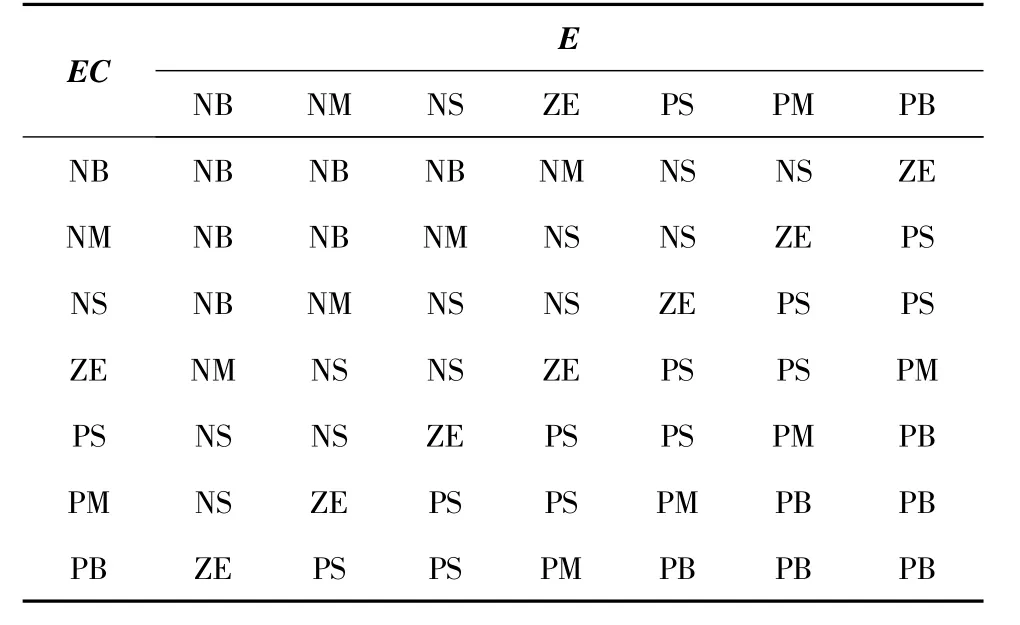
表1 模糊控制规则表Table 1 Regulations of fuzzy control

2.3 模糊量的清晰化

经过模糊推理决策，整定的输出量要进行清晰化取得精确值以计算输出控制量，即热水调节电动阀的开度。常用的清晰化方法包括最大隶属度法、重心法、中心平均法等。该控制器中采用中心平均法求取输出量的精确值。

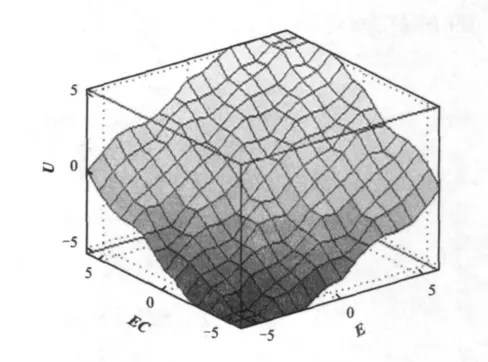
图4 模糊控制规则表面Fig.4 Rules surface of fuzzy control

中心平均法既避开了求取隶属函数的积分运算，同时又考虑了各模糊集合对精确值的影响。该方法计算较简单，清晰化的鲁棒性较好，是模糊推理系统中常用的方法［7］。中心平均去模糊化方法公式:

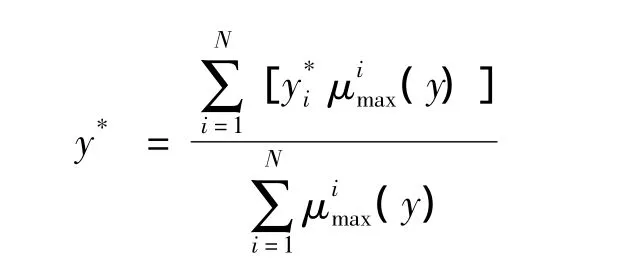
3 模糊控制器应用

热交换器系统模型可以用纯滞后环节和一阶惯性环节表示。对于水污染防治生物处理技术实验室验证评估过程中的热交换系统，函数模型可表示如下:

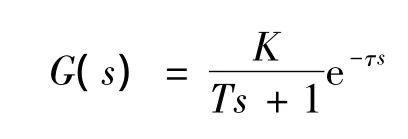
式中，K为增益系数，取值5;T为时间常数，取值3500 s;τ为滞后时间，取值200 s;s为时间变量。

在Matlab7.0工作环境下，利用模糊推理系统编辑器建立一个fis文件，定义为flc.fis。在Simulink仿真环境下，根据图2的模糊控制器结构利用工具箱编辑系统框图，输入为偏差论域E和偏差变化率论域EC，输出为温控系统模型输出，并增加积分环节与模糊控制器输出进行叠加，以消除静态误差，然后与被控对象温控系统的模型相连接，输出反馈到控制器输入端，得到控制器与一阶滞后被控对象组成的控制系统仿真框图，如图5所示。

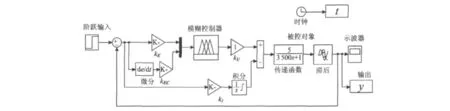
图5 模糊自调整控制系统仿真Fig.5 Simulation block diagram of fuzzy self-adjustment control system

4 仿真结果与分析

在单位阶跃输入下，通过调整量化因子(kE，kEC)和控制增量比例因子(kU)，可得到比较理想的模糊控制仿真结果。kE取值1.35，kEC取值0.98，kU取值1.05，kI取值0.0016。对积分环节采取限幅，该次仿真实验中限幅为0.2。利用仿真参数对话框，设置相关的仿真参数，仿真时间设置为5000 s，采样周期设置为1 s。对热交换器分别采用常规PID控制器和模糊自调整控制器进行调节，其中PID控制器参数按临界比例法［13］进行调整，两种控制器系统的单位阶跃响应如图6所示。

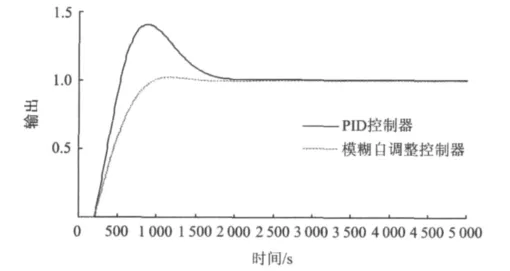
图6 两种控制器系统的单位阶跃响应Fig.6 Response of two control system on step signal

由图6可知，利用模糊自调整控制器与比例积分环节控制量叠加后，可消除静差，减小超调量，响应速度快，调节时间短。与常规PID控制器相比，模糊自调整控制器具有良好的快速性和鲁棒性，提高了系统的动、静态性能。

5 结语

针对大滞后的温度控制系统，与常规PID控制器相比，采用模糊自调整控制器可以使系统的动态性能和稳态性能得到改善，具有良好的控制效果。但通过仿真结果可以看出，控制器缺乏较强的自适应能力，系统仍有一定的超调量。因此，在今后研究中考虑综合神经网络、遗传算法的智能控制器，在线训练模糊规则、调整量化因子等，以优化温控系统的动态性能和鲁棒性，实现控制目的。

［1］陶永华.新型PID控制及其应用［M］.北京:机械工业出版社，2002.

［2］孙增圻.智能控制理论与技术［M］.北京:清华大学出版社，2003.

［3］易继锴，侯媛彬.智能控制技术［M］.北京:北京工业大学出版社，2003.

［4］YANG X H，LIU T R，SUN J.Optimal PID control of heat exchanger temperature［J］.Advanced Materials Research，2011，204/205/206/207/208/209/210:21-24.

［5］PADHEE S，SINGH Y.A comparative analysis of various control strategies implemented on heat exchanger system:a case study［C］//Proceedings of the World Congress on Engineering:Ⅱ.London:International Association of Engineers，2010.

［6］MAIDI A，DIAF M，CORRIOU J.Optimal linear PI fuzzy controller design of a heat exchanger［J］.Chemical Engineering and Processing，2008，47(5):938-945.

［7］MAZINAN A H，SADATI N.Fuzzy predictive control based multiple models strategy for a tubular heatexchanger system［J］.Applied Intelligence，2010，33(3):247-263.

［8］ARTURO P，CLAUDIA R，KEVIN P，et al.On-line fuzzy-logicbased temperature control of a concentric-tube heat exchanger facility［J］.Heat Transfer Engineering，2009，30(14):1208-1215.

［9］ ŞAHIN ŞENCAN A，KILIÇ B，KILIÇ U.Optimization of heat pump using fuzzy logic and genetic algorithm［J］.Heat and Mass Transfer，2011，47(12):1553-1560.

［10］MAZINAN A，SADATI N.Fuzzy multiple models predictive control of tubular heat exchanger［C］//2008IEEE World Congress on Computational Intelligence. Piscataway:IEEE Press，2008:1845-1852.

［11］HABBIA H，KIDOUCHEA M，KINNAERTB M，et al.Fuzzy model-based fault detection and diagnosis for a pilot heat exchanger［J］.International Journal of Systems Science，2011，42(4):587-599.

［12］TABATABAEE S，ROOSTA P，SADEGHI M S，et al.Fuzzy PID controller design for a heat exchanger system:the energy efficiency approach［C］//International Conference on Computer Applications and Industrial Electronics(ICCAIE). Los Alamitors:IEEE Computer Society Press，2010:511-515.

［13］李园，李平.填料塔热交换系统的模糊模型PID优化控制［J］.工业仪表与自动化装置，2006(5):50-53.○