OFDM 中改进的基于循环前缀的ML 迭代同步算法

孙文胜 ，潘婷婷

(杭州电子科技大学通信工程学院，杭州310018)

准确的同步是实现OFDM 系统的关键技术之一［1，7］。在OFDM 系统中有关定时和频率偏差估计的同步算法主要有两类:一类是数据辅助估计，即非盲估计，它基于导频符号来实现估计［8］。另一类是非数据辅助估计，即盲估计，它是利用构造信号的结构(如基于循环前缀和虚拟子载波)进行估计，这类算法克服了导频符号浪费信道资源的缺点［2］。

基于CP(Cyclic Prefix，循环前缀)的算法，最大特点是巧妙地利用了CP 的特性，不需要额外的冗余信息来同步［4］。1997 年，Van de Beek 提出了基于CP 的最大似然(ML)估计算法［3］，该算法的频偏估计范围小，定时估计较为粗糙，并且在多径信道下性能较差，很难直接应用到实际OFDM 系统当中。文献［5］提出利用数据帧内各个OFDM 符号的CP分别进行频偏估计的算法，，该算法虽然能够较好地纠正每个OFDM 符号内的残余频偏，但其算法复杂度较高。本文基于原有的最大似然(ML)迭代算法［6］，提出了一种改进的基于CP 的ML 迭代同步算法。

1 OFDM 系统模型

在发送端首先进行数字调制生成复信号Xn，通过傅立叶反变换IFFT 将信号调制到N 个子载波上得到时域信号为

然后进行并串转换以及插入长为Ng的CP，构成一个长为N+Ng的OFDM 符号。经过多径衰落信道后，受时延、频偏以及高斯噪声的影响，实际接收信号应为

式中，L 为信道的多径数目;αi为第i 径信道的衰落系数;τi为第i 径的延迟样点数，d，ε 分别为时延样点数和频率偏移，w(n)为离散加性高斯白噪声。

2 基于循环前缀的迭代ML 同步算法

2.1 传统的基于循环前缀的ML 同步算法

Van de Beek 等提出了利用OFDM 的CP 特性，在时域进行联合的定时和频率估计算法。为了克服多径效应，引入了CP 作为保护间隔。CP 是信息符号中部分数据的重复，显然，与这部分数据存在较大的相关性，利用这个区别来得到符号定时d 和频率偏差ε 的最大似然估计算法。其基本原理是计算在(d，ε)二维空间中各个取样值的后验概率的最大值。能量项r(d)，Φ(d)为

式中，r(n)表示接收到的信号，r*(n)表示取共轭，d表示CP 中最后一个采样点的位置，ε 为归一化最小频率偏差。

最大似然函数为

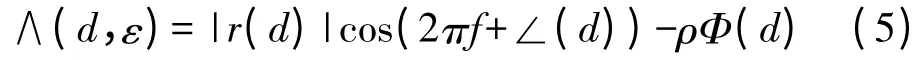
式中，∠表示取相位。ρ 为r(n)和r(n+N)之间的相关系数的幅度，和分别表示信号和噪声的方差，SNR 表示信噪比，定义SNR=。式(5)的ρ 可由式(6)得到:

由此得到的定时偏差d 和频率偏差ε 的最大似然估计为:

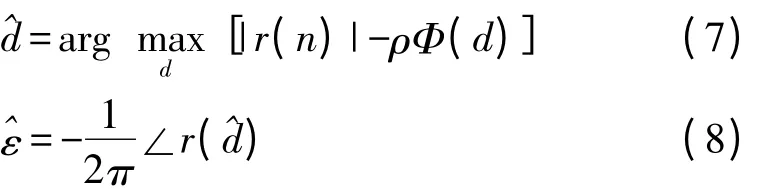
上述ML 方法，如果只考虑N+2Ng个抽样值，则在式(5)中求解最大值的范围分别为d∈［0，Ng］和ε∈［－0.5，0.5］。从上述分析可知，ML 算法具有计算量小、冗余度低、算法实现简单且具有可同时估计定时偏差和频率偏差的优点。但是，该算法的频率偏差估计范围小，定时估计较为粗糙，很难直接应用到实际OFDM 系统当中。

2.2 基于循环前缀的ML 同步迭代算法

利用ML 算法与迭代技术相结合，使式(5)中的2 个变量分离，最后达到最大化的目的。由于频率偏差ε 是连续的，而定时偏差d 是离散的且存在有限个抽样值，所以选择d 作为迭代过程的迭代变量比选择ε 要好。

在第j 次抽样中，选择d0，j为迭代起始点，定义di，j，εi，j分别为第i 次迭代的定时偏差和频率偏差，其中j=0，1，…，N+Ng－1。则式(8)可写为:

式(9)中计算所得的ε1，j代入最大似然函数式(5)，则式(5)改为;

式(10)中只含有一个变量d，于是可得

式(11)中得到的di，j代入式(9)重复上述过程，得到ε2，j，d2，j，ε3，j，d3，j，…，如此计算下去直到dn，j=dn+1，j，迭代过程结束。其迭代过程可简单表示为d0，j→ε1，j→d1，j→ε2，j→…→εn，j→dn，j→εn+1，j→dn+1，j，until dn，j=dn+1，j。

其间得到许多迭代收敛对(di，j，εi，j)。设最后得到的迭代收敛对为(dn，j，εn，j)，其中，εn，j，将其代入式(5)计算其值，得:

则在集合{C0，C1，…，CN+Ng－1}中对应于最大值的迭代收敛对即为所求。从以上的迭代过程看出，需对所有抽样点进行迭代计算，这样做计算量大、用时多，而且存在较大的冗余，所以需要寻求一种简化的方法。

3 改进的基于循环前缀的ML 同步迭代算法

在频率选择性信道中，多径效应使得OFDM 符号在时间轴上被扩散，CP 的前面一部分采样点被码间干扰ISI(Inter Symbol Interference)所污染，这时的相关峰值就不明显。因此，有必要对符号同步粗估计，对得到的FFT 窗口位置进一步地限制，其允许的范围由CP 长度Ng和多径信道弥散长度L 共同决定。

3.1 对相邻多个符号多点相关求均值

循环前缀的起点和数据区的起点虽然存在一定差异，但是考虑到噪声的存在，这种差异就可能被淹没，而传统的ML 算法采用单点求相关值，势必造成影响。因此，考虑联合M 个点求相关值取其平均。这里，M 的取值有一定的讲究，取得太大会加大算法的复杂度，取得太小效果不明显。

对于多径衰落信道，选取信道变换相对缓慢以及相关性大的符号，因此，根据最大多径时延τmax最大多普勒频移fd来确定，M 取⎿1/(2fdT)」和⎿1/(τmaxFc)」的最小值比较合适。其中，T 为OFDM 的符号间隔，Fc为子载波间隔，⎿」表示向下取整。因此，可以根据CP 长短和最大多径时延来决定其大小。在SNR 比较高、多径延时也不很明显的情况下，可以缩小M;反之，可以取得大些。这样做考虑了信道对相关值的影响从而使得抽样点的幅度变化进一步变小，使迭代算法的估计值更加准确。因此，最大似然求相关的表达式改为

在信道衰落严重的情况下，考虑在一个OFDM 符号内多点平均求相关值，减少噪声的影响，以降低突发性相关尖峰的概率，式(13)可写为:

其中，P 表示同一符号中的连续点的个数。

3.2 减少参与运算的CP 长度

在多径衰落信道中，循环前缀的一部分抽样点会受到ISI 影响，使得r(d)的值发生改变，从而影响整个迭代算法的准确程度。由于多径时延和多普勒频移，CP 中只有Ng－τmax个点没有被污染，因此，在运算的时候，不是把所有的CP 都包括在内，而是去掉绝大多数被多径干扰的CP，在本文算法中，取1/4 的CP 长度。实际应用中，可根据SNR 和最大多径时延调整参与运算的CP 长度。则式(13)可写为:

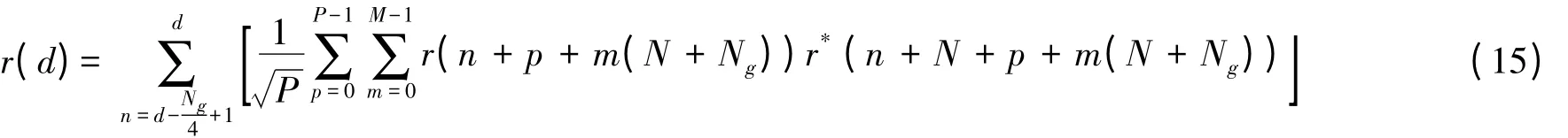
3.3 迭代间隔D 的研究

从以上的迭代过程看出，需对所有抽样点进行迭代计算，这样做计算量大、用时多，而且存在较大的冗余，需要寻求一种简化的方法。所以，选择迭代起始点以长度D 作为间隔，也就是说选择d0，j，d0，j+D，d0，j+2D，…进行迭代即可。

这个D 的长度选择是关键问题，取得太小，对降低算法复杂度效果不明显，取得太大，会降低估计精度，所以，必须在算法复杂度和精度之间权衡。由于噪声和多径影响，每个符号的最大迭代长度D 是不同的。这种现象如图1 所示，显示了前30 个符号的最大迭代长度。由图1 可知，每个符号的最大迭代长度是不同的。如果我们可以找到最适合的迭代长度D，只需计算d0，j，d0，j+D，d0，j+2D，…，就足以得到准确的定时偏差和频率偏差。

图1 每个符号的最大迭代长度

为准确估计不同的迭代长度D，在帧数大于1000 时，我们分别选取N 和Ng不同值的OFDM 系统作系统仿真。N 和Ng不同的OFDM 系统中迭代长度D 由表1 和图2 所示。

表1 N 和Ng 不同的OFDM 系统中迭代长度D 的取值

图2 Ng 和迭代长度D 的关系

由图2 可见，准确的迭代长度D 几乎与循环前缀的长度Ng成线性正比关系。因此，选择确切的迭代长度D=Ng，可以在保证取到最大迭代收敛对，取得准确的定时和频率偏差的同时，最大限度的降低算法复杂度

3.4 改进的基于CP 的ML 同步迭代算法

根据以上改进点及采取的改进方案，可得到改进的ML 迭代算法，其步骤总结和算法流程图如图3所示。

图3 改进的ML 迭代算法流程图

(1)选择初始化变量d0，j。并令j=0。

(2)将变量d0，j代入式(15)计算得r(d0，j)，接着由式(11)～式(13)求出对应的迭代收敛对

(3)将得到的迭代收敛对代人式(12)，来确定最大似然函数Cj的值。

(4)令j=j+Ng，若j≤N+Ng－1，则返回执行步骤(2);否则执行下面的步骤(5)。

(5)从所有由步骤(3)得到的Cj值中确定最大值Cmax，则与之对应的迭代收敛对为即为要求的定时偏差和频率偏差。

4 仿真及性能分析

以MSE 为准则来实现本文算法与原迭代算法的性能比较。仿真中所用的参数为:子载波数N=1024，循环前缀Ng=256，子载波调制方式为QPSK。在改进的算法中，M 取值为6。信道模型:4 径衰落，多径之间指数衰落，每径延迟70 个采样点。在多径衰落信道下比较原迭代算法与本文算法的性能。

图4 和图5 分别为在多径衰落信道对定时偏差和频率偏差估计的性能。由图4，经比较，可看出，对于定时偏差的估计，两者曲线的走势相近，几乎不相上下，随着信噪比的增大，比原迭代算法估计精度略有提高，但是，本文算法的复杂度要相对低得多。由图5，可看出，对于频率偏差的估计，本文算法比原迭代算法估计精度要高，性能较好。

图4 定时偏差的均方差的比较

图5 频率偏差的均方差的比较

可见本文算法对定时偏差和频偏的估计比原算法的性能都要好，并且算法复杂度较低，这是因为原迭代算法使用CP 的所有采样点，而CP 的一部分采样点因为多径效应受到干扰，影响估计精度。而本文算法优越的原因是采用多点相关求均值，且去掉了由于多径影响受干扰的CP 部分，从而提高了估计精度。

5 总结语

本文对于基于CP 的ML 迭代同步算法进行了改进，得到了一种可在多径衰落信道下获得较准确的定时估计和频率偏差估计的迭代算法。本算法考虑到多径信道的影响，利用多个OFDM 符号多个抽样点相关求均值，去掉了CP 受多径干扰的部分，达到增加同步估计精度的目的。并且提出迭代间隔D，有效的降低了算法复杂度。仿真结果表明，本文算法能够有效的提高估计精度，有效的降低了算法复杂度。

［1］ 王文博，郑侃.宽带无线通信OFDM 技术［M］.北京:人民邮电出版社，2003.

［2］ 佟学俭，罗涛.OFDM 移动通信技术原理与应用［M］. 北京:人民邮电出版社，2003.

［3］ van de Beek J J，Sandell M，Borjesson P O.ML Estimation of Time and Frequency Offset in OFDM Systems［J］.IEEE Transactions on Signal Processing，1997，45(7):1800－1805.

［4］ 唐彦波，葛万成，龚国强. 多径衰落信道下的正交频分复用符号同步算法［J］.同济大学学报，2009，37(8):1096－1099.

［5］ 彭小勇，肖悦，李少谦. 一种新的基于循环前缀的残余频偏纠正算法［C］//现代化电子信息技术理论及应用，2005.

［6］ 吴国庆.基于迭代ML 算法的OFDM 同步技术［J］. 现代电子技术，2008，31(1):36－37，40.

［7］ 马杨军，胡耀明.OFDM 通信系统中符号同步的优化设计［J］.电子器件，2009，32(4):781－787.

［8］ 毛剑慧，乔树山，吴斌.一种可靠的OFDM 系统时间和频率同步方案［J］.电子器件，2008，31(3):955－958.