球谐波展开法求解玻尔兹曼传输方程综述

郭 爽，李建清

(电子科技大学物理电子学院，成都610054)

在半导体产业发展初期，采用宏观的漂移扩散模型或流体力学模型能够很好地模拟器件的性能。最近几十年，由于半导体器件特征尺寸的不断缩小，漂移扩散模型或流体力学模型已经不能够准确地描述其传输特性。如果忽略量子力学效应，半经典的玻尔兹曼方程(BTE)是半导体器件中载流子传输特性及其分布最好的数学描述，它能够比较准确地描述电子的微观行为［1－4］。常用的直接求解BTE 的方法主要有蒙特卡洛(MC)法和球谐波展开(SHE)法。MC 法从微观的角度把半导体器件中的载流子看成分立的个体，主要研究载流子的个体行为，通过模拟一个随机过程来求解BTE。MC 法非常灵活，而且可分析复杂的能带结构和散射过程，不需要做很多近似，因此广泛应用于器件模拟［7］。但由于MC 法的随机特性，该方法具有很多缺陷，比如，计算量大，很难模拟小事件和小信号分析，小电流下需要很大的CPU 时间等。另一种直接求解BTE 的方法是SHE 法，SHE 法对BTE 进行球谐波展开，离散后获得代数矩阵方程，从而求得BTE 的确定解。SHE 法能够提供整个器件的分布函数，不依靠迁移率模型，不易受统计噪声的影响，避免了MC 法的随机性缺点，并且能够保存载流子能量分布的信息，而且计算量比较小，尤其在小信号分析和噪声分析中，SHE 法比MC 法更有优势［1－6］。长时间以来，由于SHE 法需要很大的内存，导致其在器件模拟方面受到限制。最近几十年，随着计算机内存和速度的指数级增长，该方法的可行性也大大增加。早在二十世纪九十年代，一阶展开的SHE 法就应用于一维器件的模拟，后来逐渐扩展到任意阶展开［8－10］和二维实空间的模拟［11－14］，并且在物理模型上也有了很大的改善，包括一些全带效应的低阶展开 ，全带结构的价带模拟［1，16］，考虑磁场作用的体硅模拟［15］，相关散射机制的MOSFET 模拟［17，19］，采用低阶展开的二维器件模拟［12，17］以及高阶展开的二维模拟［13］。为了克服高阶展开的巨大内存需要，尤其是对于二维、三维器件，K. Rupp 等提出了压缩矩阵存储定理［3］。通过结合有限体积法数值离散方法以及迎风差分、H－转换以及最大熵消散(MEDS)等数值稳定技术［1，3－4，8，23］，大大地改善了高阶SHE 解的稳定性。

1 玻尔兹曼方程(BTE)

BTE 用于研究半导体中非平衡状态下电子的分布函数，可得到不同条件下电子的分布函数f(→，→，t)，进而能够求出电子的各种输运参量。BTE 形式如下:

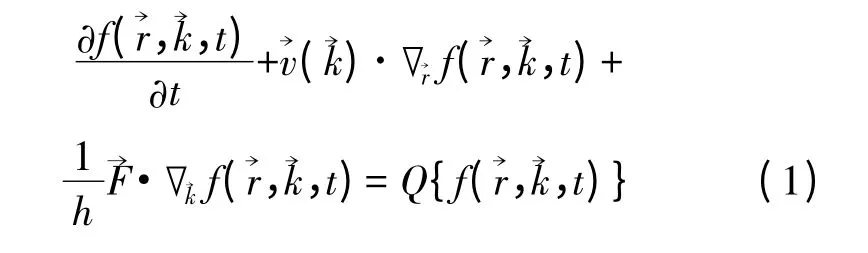
其中Q 为散射算符，由各种散射机制的散射率s确定:

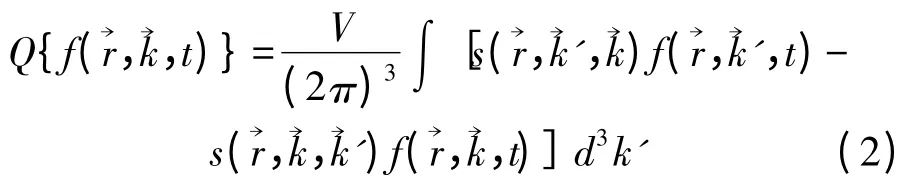
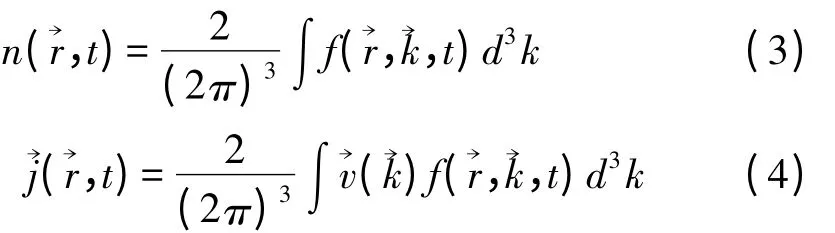
利用SHE 法求解BTE 主要有3 种方法:项匹配法、Galerkin 方法和投影法。下面分别介绍这3 种方法。

2 项匹配法

将分布函数在实空间中每一点展开为一系列球谐波加权求和:

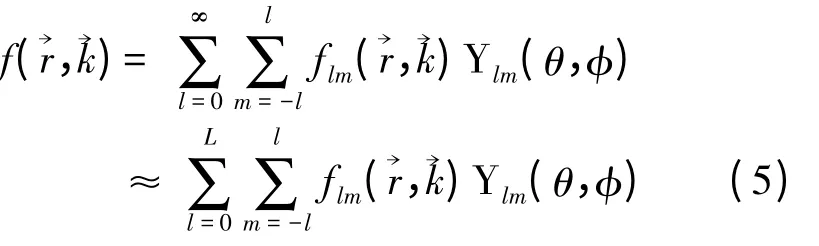
考虑一维实空间 ，以极坐标表示的二维动量空间(k，θ)，由于分布函数关于电场的对称性，球谐波函数退化为勒让德多项式，与φ 无关，即:

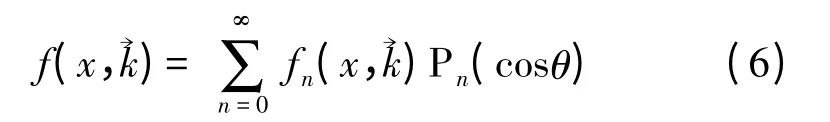
将分布函数插入到BTE 中，通过匹配相同谐波阶数的展开项，得到一系列以展开系数为未知量的耦合偏导方程［11－12］，最后离散偏导数方程组得到关于展开系数fn(x，→)的代数方程组。如果将分布函数展开到一阶，即n 分别取0 和1 则得到［8］:

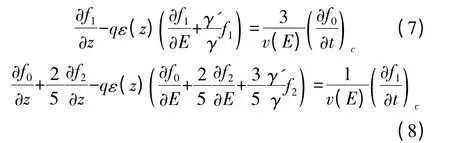
文献［11，24］对分布函数展开到一阶得到的以上两个偏导方程式进行了离散。图1 为文献［20］中采用项匹配法求解BTE，模拟硅中电子传输得到的两个结果图，左右两个图分别是在电场为70 kV/cm 和500 kV/cm 时，将分布函数展开到一阶球谐波得到的分布函数随能量的变化曲线，并与MC 法对比的结果。从图中可以看出，包括二阶谐波展开系数能够得到与MC 法非常接近的结果，并且在较高的能量下，MC 法引入了数值噪声(如图1(a))，而采用SHE 法能得到稳定的结果。

项匹配法存在的问题是，偏导方程组由展开阶数决定，展开阶数必须提前确定，而且如果要求高阶解，则必须重新对方程进行展开和离散，过程繁琐，很难扩展到任意阶展 另一方面，高阶展开对器件传输特性的模拟是非常重要的，如果忽略一些高阶展开将会影响结果的准确性。

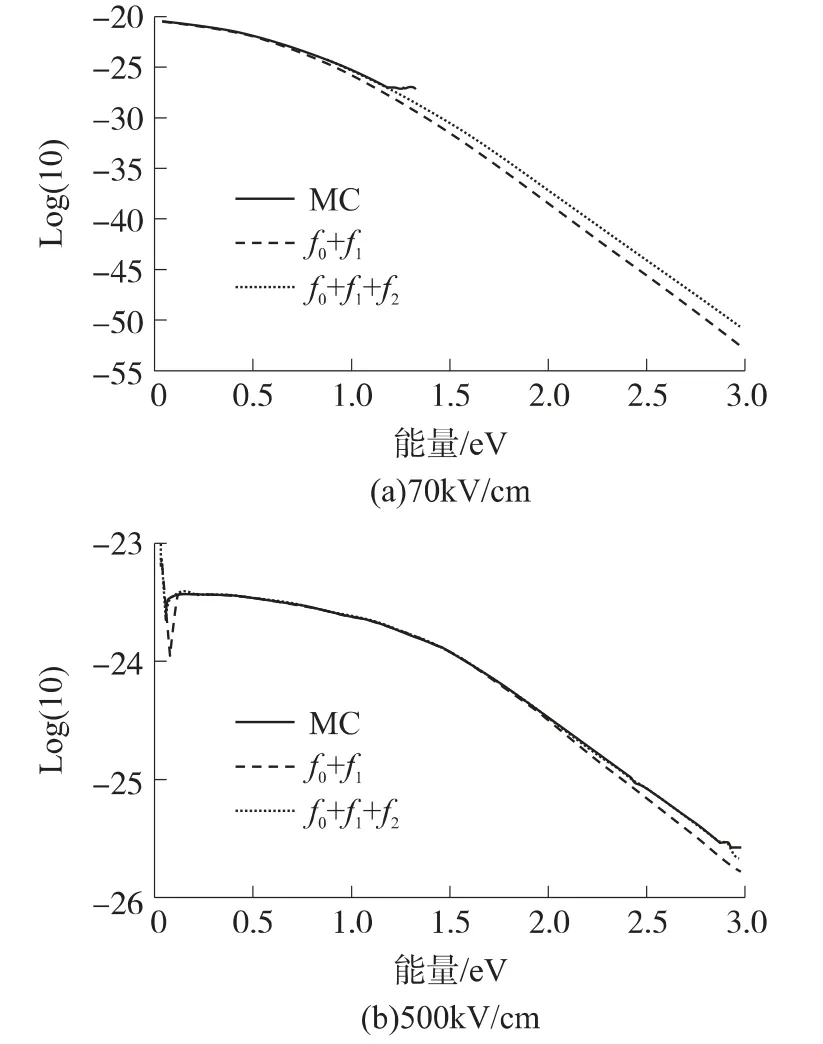
图1 MC 方法和项匹配法得到的分布函数随能量的变化

3 Galerkin 方法

Galerkin 方法的思路是将分布函数展开为球谐波函数之和，并将球谐波展开插入到BTE 中，然后对BTE 的每一项同乘以球谐波函数的共轭，并在整个动量空间进行单位球积分，最后采用有限差分法在能量和实空间对展开系数进行离散，得到以谐波展开系数为未知量的代数矩阵方程［8，21］:

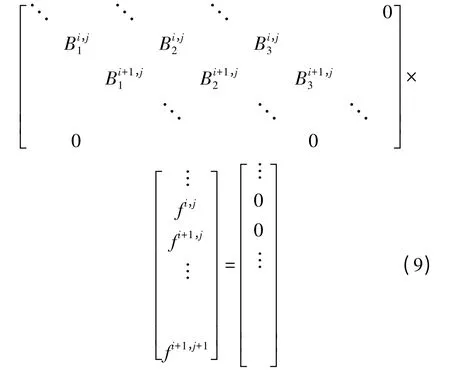
以上矩阵方程中，f 为能量－空间网格中任意给定一点的未知球谐波系数矢量。矩阵方程的右端取决于散射机制和边界条件。对分布函数展开系数对能量和实空间方向的导数采用不同的差分格式离散，在不考虑数值稳定性的情况下，仅仅影响非零矩阵块在矩阵中的位置。

Khalid Rahmat 等作者在文献［21］中利用Galerkin 方法模拟一维N+NN+管，采用单边两点近似，对于偶数谐波展开系数对能量和空间方向的求导采用前向差分，而对于奇数谐波展开系数对能量和空间方向的求导采用后向差分。尽管该差分定理在大多数情况下是稳定的，但是在N+N 结处出现了不稳定。针对单边差分格式存在的不稳定性，Khalid Rahmat 等作者在文献［8］中提出了一种解决方法，即采用迎风格式的差分来离散展开系数对能量的导数。当电场为正时，奇数谐波系数对能量的求导采用前向差分，偶数对能量的求导采用后向差分;当电场为负时，奇数谐波系数对能量的求导采用后向差分，偶数对能量的求导采用前向差分。图2为分别采用迎风离散和单边离散得到的关于能量的一阶谐波系数对比图。图3 为在N+NN+管的实空间方向两点处，分别展开到一阶和三阶得到的分布函数。由图2 和图3 可以看出，相比低阶展开，高阶展开能够得到更加圆滑的分布函数，同时，迎风格式的差分离散大大提高了SHE 解的稳定性。

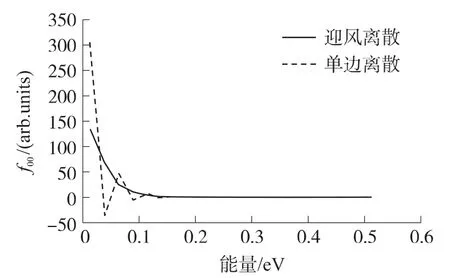
图2 单边和迎风离散得到的f0 对比图

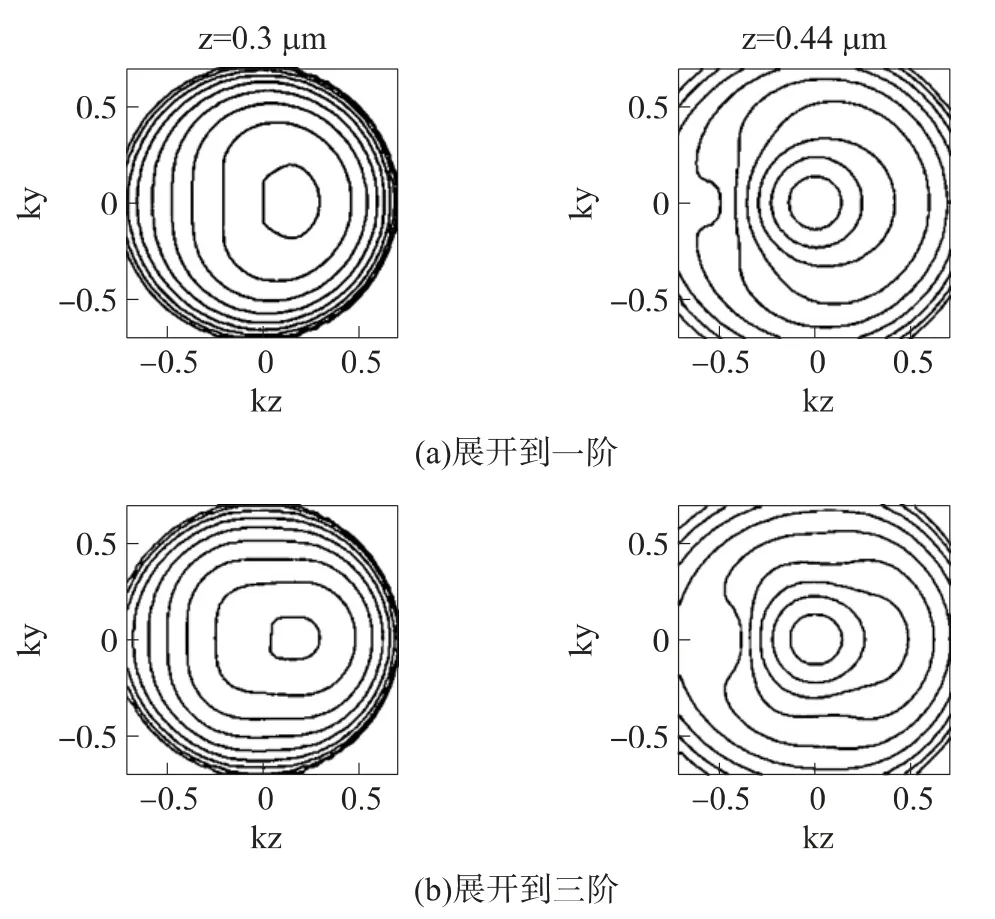
图3 一阶和三阶展开得到的分布函数

Galerkin 方法的优点在于更高阶展开只增加代数方程组产生的系数矩阵的大小，而对于项匹配法，高阶展开不仅会扩大耦合偏导方程组而且需要对其进行重新离散。Galerkin 方法允许在不同的空间区域采用不同的展开阶数，而且将球谐波展开阶数作为程序的一个输入参数，便于检验高阶展开对于器件模拟结果的影响［8］。

4 投影法

投影法的思路是利用球谐波函数将BTE 投影为以分布函数展开系数与一般状态密度乘积为待求解的平衡方程:即将BTE 转化为球谐波方程，并在能量空间和实空间中利用有限体积方法对球谐波方程离散。投影法将分布函数展开为关于能量的函数，其优点为由于热平衡时的分布函数在等能面上是各向同性的，在许多散射模型中，散射率是能量的函数而且散射期间能量转换也是常数，从而散射积分在等能面上可以很容易的计算出来。因此分布函数在等能面上的展开比起关于波矢的模的展开有许多优点［1］。

为了在等能面上展开分布函数，需要在能量空间与波矢空间建立一种映射关系，根据这种转换关系，利用微观量投影表达式［1，22］，将BTE 在等能面上投影为关于展开系数与一般状态密度乘积的球谐波方程，详细的推导过程可参见文献［2］，得到球谐波方程:

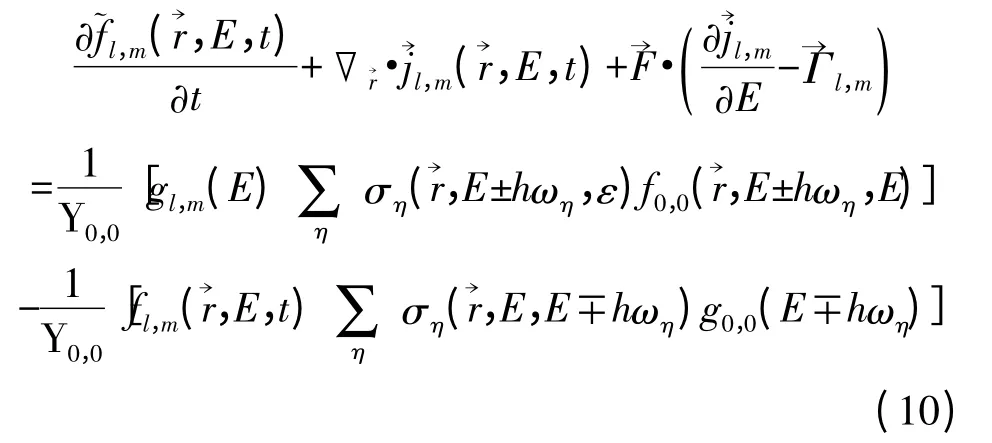
为了得到稳定的SHE 解，文献［1－2］采用MEDS，引入熵函数

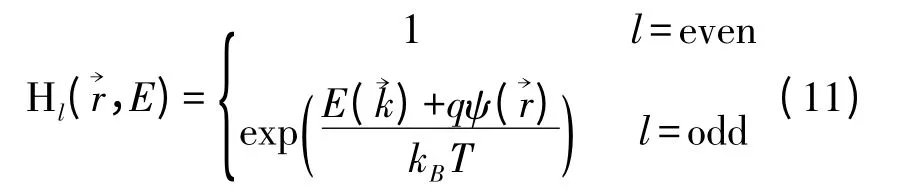
在球谐波方程(10)两边同时乘以熵函数(11)，得到:

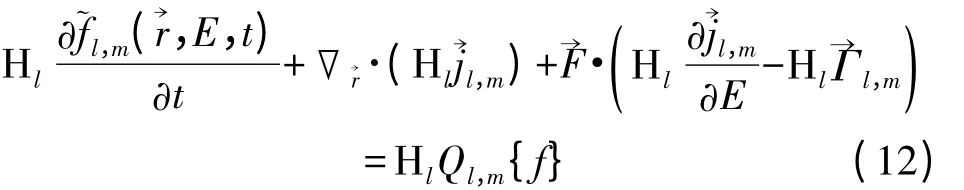
从而将球谐波方程(10)划分为奇偶两部分。对稳定后的平衡方程(12)采用有限体积法［2］在能量和实空间中进行离散，保证BTE 的粒子数守恒特性。

由于数值稳定性问题主要与空间偏导与其他变量导数之间的耦合有关，而平衡方程中既有对空间变量的偏导，又有对能量的偏导，从而会导致数值不稳定。文献［4］采用H－转换，即将其中，H=ε－ψ(r)表示电子总能量，ψ(r)为电子静电势。该方法相对于MEDS 的优势在于即使在弹道限制下也能准确的处理自由流算符，但是存在的不足是引入了与电势有关的能量网格。

C.Jungemann 等作者在文献［9］中采用投影法以及MEDS 和H－转换模拟了一维N+NN+。图4 为将球谐波展开到一阶和九阶时得到的电流随外加偏压的变化以及相对误差。由图可以看出，电流作为外加偏压的函数，在小偏压下一阶展开就已经出现比较大的相对误差，主要原因是N+NN+内部存在的内建电场，导致了准弹道传输 因此， 展开的最大阶数对于器件传输特性具有较大的影响。

图4 展开到一阶和九阶时的电流和相对误差

目前存在5 种能带模型可以用于SHE 法，分别是:Modena 模型［27］、Vecchi 模型［6］、各向异性模型［25］、扩展的Vecchi［26］模型以及全带模型。S.－M.Hong 等作者在文献［22］中采用投影法模拟N+NN+管，图5 ～图7 为采用Modena 模型、扩展的Vecchi模型以及全带模型得到的电流、电子速度和电子能量的分布图，并与全带结构的蒙特卡洛(FBMC)法比较结果。从图中可以看出，扩展的Vecchi 模型和FBMC 法取得了基本一致的模拟结果，但是仍然存在略微的差异，主要原因就是对能带结构做出的近似。文献［25］中采用各项异性能带结构的投影法模拟N+NN+管，该能带结构模型能够准确的模拟碰撞电离等高能效应，并且可以得到与FBMC 法基本吻合的模拟结果。

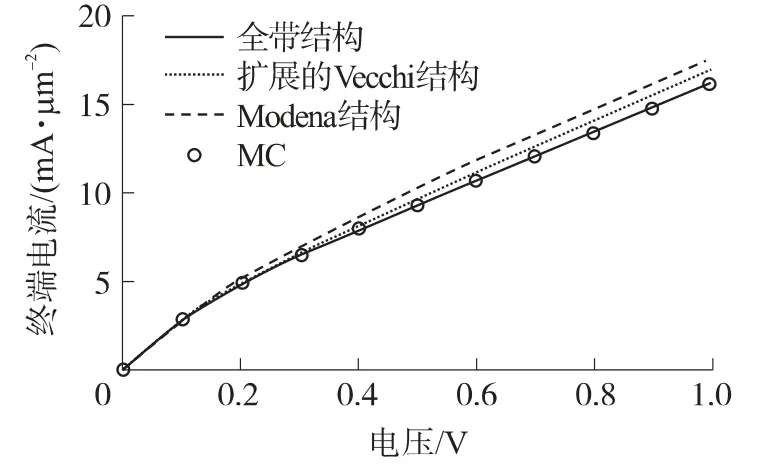
图5 不同能带模型以及MC 方法得到的终端电流

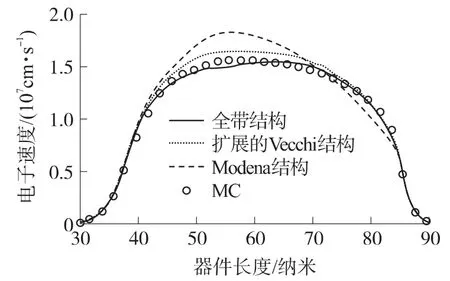
图6 不同能带模型以及MC 方法得到的电子速度图

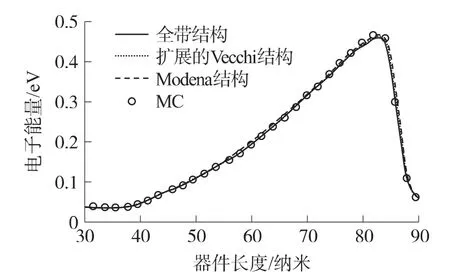
图7 不同能带模型以及MC 方法得到的电子能量

由此可以看出，各向异性模型、扩展的Vecchi 模型以及全带模型都能取得与FBMC 法相一致的模拟结果，全带模型得到的结果更加接近FBMC 法。Modena 模型不能准确的描述高场传输和碰撞电离。Vecchi 模型由于受限于最低阶的展开不适合于短沟道器件终端电流的计算。各向同性的扩展的Vecchi模型在计算热载流子特性和终端特性方面比Modena模型准确，并且不需要额外的内存和CPU 时间。从数值效率上比较，各向异性模型存在的不足是增加了耦合项的数目，从而导致需要的内存增大。全带模型在取得与最简单的Modena 模型相同的CPU 效率的同时，能够得到比其他能带模型更准确的模拟结果。因此，从物理准确度和数值效率两方面考虑，全带模型是最好的选择，扩展的Vecchi 模型次之［22］。

5 总结

用于直接求解BTE 的项匹配法、Galerkin 法以及投影法的共同点是将分布函数展开为一系列球谐波函数之和。不同之处在于前两种方法是将分布函数展开为关于波矢模的展开系数与球谐波函数乘积之和，而投影法是展开为关于能量的展开系数。而且项匹配法和Galerkin 法得到的是以球谐波展开系数为待求解的代数矩阵方程，但是投影法是将最初的连续方程转化为网格点上以球谐波展开系数与一般状态密度之积为待求解的离散的代数矩阵方程。目前，投影法作为求解BTE 的一种SHE 方法得到了广泛的应用，主要是由于高阶展开能够准确的描述器件的弹道效应和高场传输特性，并且该方法能够结合MEDS 和H－转换稳定技术，从而大大地改善SHE 解的数值稳定性。

［1］ Jungemann C，Pham A T，Meinerzhagen B.Stable Discretization of the Boltzmann Equation Based on Spherical Harmonics，Box Integration，and a Maximum Entropy Dissipation Principle［J］.Journal of Applied Physics，2006，100(2):024 502－024502－13.

［2］ Rupp K. Numerical Solution of the Boltzmann Transport Equation using Spherical Harmonics Expansions［D］.Dissertation of Master，Vienna University of Technology，2011.

［3］ Rupp K，Jüngel A，Grasser T. Matrix Compression for Spherical Harmonics Expansions of the Boltzmann Transport Equation for Semiconductors［J］. Journal of Computational Physics，2010，229(23):8750－8765.

［4］ Hong S M，Jungemann C，Bollhöfer M.A Fully Coupled Scheme for a Boltzmann－Poisson Equation Solver Based on a Spherical Harmonics Expansion［J］.Journal of Computational Electronics，2009，8(3):225－441.

［5］ Jungemann C，Meinerzhagen B.Analysis of the Stochastic Error of Stationary Monte Carlo Device Simulations［J］. IEEE Trans.Electron Devices，2001，48(5):985－992.

［6］ Vecchi M C，Rudan M.Modeling Electron and Hole Transport with Full－Band Structure Effects by Means of the Spherical－Harmonics Expansion of the BTE［J］.IEEE Trans.Electron Devices，1998，45(1):230－238.

［7］ 王祖军，刘书焕，唐本奇，等.SiGe HBT 器件特征参数的数值模拟与分析［J］.电子器件，2009，32(3):534－537.

［8］ Rahmat K，White J，Antoniadis D A. Simulation of Semiconductor Devices Using a Galerkin/Spherical Harmonic Expansion Approach to Solving the Coupled Poisson－Boltzmann System［J］. IEEE Trans.Computer－Aided Design of Integrated.Circuits and Systems，1996，15(10):1181－1196.

［9］ Jungemann C，Hong S M，Matz G.High－Order Spherical Harmonics Solution of the Boltzmann Equation and Noise Modeling［C］//International Workshop on Computational Electronics (IWCE)，2010:1－6.

［10］ Wu Y J Hennacy K，Goldsman N，Mayergoyz I. Two Dimensional Submicron MOSFET Simulation Using Generalized Expansion Method and Fixed Point Iteration Technique to the Boltzmann Transport Equation［C］//VLSI Technology，Systems，and Applications，Proceedings of Technical Papers，1995:122－126.

［11］ Ventura D，Gnudi A，Baccarani G.Multidimensional Spherical Harmonics Expansion of Boltzmann Equation for Transport in Semiconductors［J］.Applied Mathematics Letters，1992，5(3):85－90.

［12］ Gnudi A，Ventura D，Baccarani G.Two－Dimensional MOSFET Simulation by Means of a Multidimensional Spherical Harmonics Expansion of the Boltzmann Transport Equation［J］.Solid State Electron.，1993，36(4):575－581.

［13］ Hong S M，Jungemann C，Bollhöfer M. A Deterministic Boltzmann Equation Solver for Two－Dimensional Semiconductor Devices［C］//Proc.SISPAD，2008:293－296.

［14］ Vecchi M C，Mohring J，Rudan M. An Efficient Solution Scheme for the Spherical Harmonics Expansion of the Boltzmann Transport Equation［J］.IEEE Trans.on CAD of Integrated Circuits and Systems，1997，16(4):353－361.

［15］ Smirnov S，Jungemann C. A Full Band Deterministic Model for Semiclassical Carrier Transport in Semiconductors［J］. Journal of Applied Physics，2006，99(6):063707－063707－11.

［16］ Pham A C，Meinerzhagen B.A Full－Band Spherical Harmonics Expansion of the Valence Bands up to High Energies［C］//Proceedings of SISPAD，2006:361－364.

［17］ Liang W，Goldsman N，Mayergoyz I.2－D MOSFET Modeling Including Surface Effects and Impact Ionization by Self－Consistent Solution of the Boltzmann，Poisson，and Hole－Continuity Equation［J］.IEEE Trans.Electron Devices，1997，44(2):257－267.

［18］ Reggiani S，Vecchi M C，Rudan M. Investigation on Electron and Hole Transport Properties Using the Full－Band Spherical－Harmonics Expansion Method［J］. IEEE Trans. Electron Devices，1998，45(9):2010－2017.

［19］ 崔强，韩雁，董树荣，等.Mos 器件二次击穿行为的电路级宏模块建模［J］.传感技术学报，2008，21(2):361－364.

［20］ Ventura D，Gnudi A，Baccarani G.An Efficient Method for Evaluating the Energy Distribution of Electrons in Semiconductors Based on the Spherical Harmonics Expansion［C］//International Workshop on VLSI Process and Device Modeling，Oiso，Japan，1991:27－29.

［21］ Khalid Rahmat，Jacob White，Dimitri A Antoniadis. A Galerkin Method for the Arbitrary Order Expansion in Momentum Space of the Boltzmann Equation Using Spherical Harmonics［C］//Proc.NUPAD V，1994:133－136.

［22］ Hong Sung－Min，Pham Anh－Tuan，Christoph Jungemann.Deterministic Solvers for the Boltzmann Transport Equation ［M］. Springer Press，2011.

［23］ Ringhofer C.Numerical Methods for the Semiconductor Boltzmann Equation Based on Spherical Harmonics Expansions and Entropy Discretization［J］.Transp.Theory Stat.Phys.，2002，31(4):431－452.

［24］ Gnudi A，Ventura D，Baccarani G.One－Dimensional Simulation of a Bipolar Transistor by Means of Spherical Harmonic Expansion of the Boltzmann Transport Equation［C］//Proceedings of SISPED，1991，4:205－213.

［25］ Hong S M，Matz G，Jungemann C A.Deterministic Boltzmann Equation Solver Based on a Higher Order Spherical Harmonics Expansion With Full－Band Effects［J］.IEEE Trans.Electron Devices，2010，57(10):2390－2397.

［26］ Jin S，Hong S M，Jungemann C.An Efficient Approach to Include Full－Band Effects in Deterministic Boltzmann Equation Solver Based on High－Order Spherical Harmonics Expansion［J］. IEEE Trans.Electron Devices，2011，58:1287－1294.

［27］ Brunetti R，Jacoboni C，Nava F，et al.Diffusion Coeffcient of Electrons in Silicon［J］. Journal of Applied Physics，1981，52(11):6713－6722.