复数域中两类函数的单值分支问题
2012-12-21冯志新
冯 志 新
(吉林师范大学 数学学院,吉林 四平 136000)
复数域中两类函数的单值分支问题
冯 志 新
(吉林师范大学 数学学院,吉林 四平 136000)
针对不同多值函数,分别运用限制辐角法和连续变化法系统地研究了对数函数与根式函数的单值分支问题.
多值函数;辐角;函数改变量;单值分支
初等多值函数是复变函数论中初等函数部分的一个重要内容[1],其解析性质和映射性质要比初等单值函数复杂得多,研究的思想方法也比较独特,学生不易理解和掌握,从而这部分内容成为该课程教学的一个难点.复变函数的解析性是以极限、连续、可微作为基础,而这些概念都是针对单值函数来说的,因此无法在原来的意义下研究多值函数的解析性.在实际应用中遇到多值函数时也只是取它的一个确定的值,因此研究多值函数的根本方法是把多值函数分解为单值函数来研究,即通过特殊的方法把初等多值函数分解为若干单值分支,进而再研究每个单值分支的连续性、解析性等性质.
对于初等多值函数,引起其多值性的主要原因是辐角的多值性,针对比较简单的多值函数,如根式函数、对数函数Lnz用“限制辐角法”将其分解为单值函数比较简单,比较复杂的一般根式函数和一般对数函数LnR(z) 用“连续变化法”分解(其中R(z)为有理函数).
1 根式函数w= (n是>1的整数)的可单值分支问题

用限制辐角的方法确定其单值分支,步骤如下:
限制辐角:令0≤ ar gz< 2π(或 -π< argz≤π)


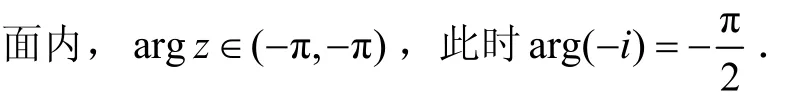
2 一般根式函数)与一般对数函数 LnR( z)的可单值分支问题
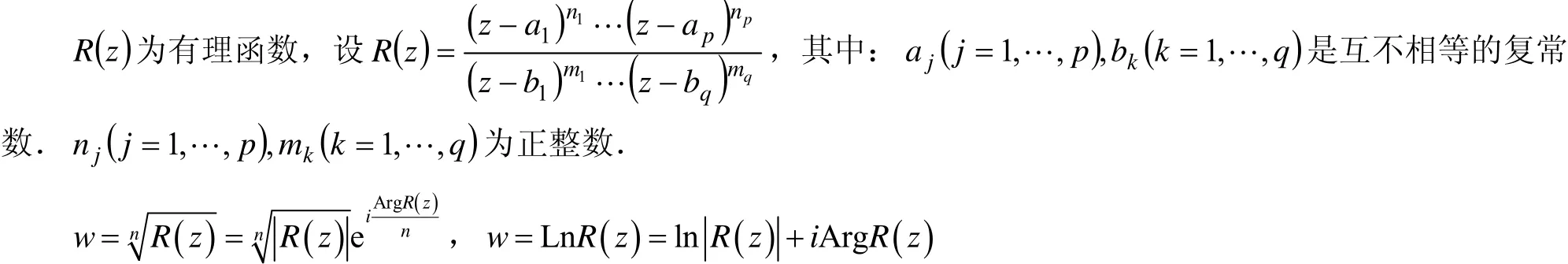
显然这两个多值函数的多值性是由 ArgR(z) 的多值性引起的,因此先研究ArgR(z)的可单值分支问题.而函数 ArgR(z) 比 Argz要复杂得多,继续用限制辐角法研究很困难,利用函数改变量研究起来思路清晰,比较容易理解.
2.1 ArgR( z)的可单值分支问题

用简单曲线l适当地连接各支点,沿l割开z平面得到的区域D就是ArgR(z)的可单值分支区域.
ArgR(z)可单值分支的确定:设D是 ArgR(z) 的可单值分支区域z0∈D,初值ϑ0=argR(z0).对于∀z∈D,在D内任意作一条连接z0,z的简单曲线L,ΔLArgR(z)= argR(z) - argR(z0),故f(z) = argR(z)= ΔLArgR(z) +ϑ0,称其为由初值ϑ0确定的单值分支.
2.2 LnR( z)的可单值分支问题

定理2LnR(z) 的支点与正常点和 ArgR(z)相同.
故 LnR(z) 的可单值分支区域与 ArgR(z)的可单值分支区域作法相同.

例2 求函数w=Ln( 1-z2)的一个可单值分支区域,并求当z=0时取值为零的分支在z=2点的值.
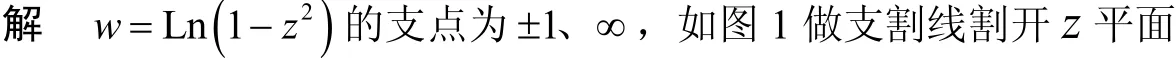
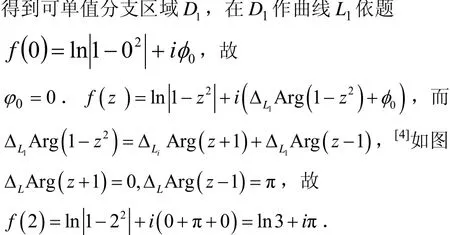
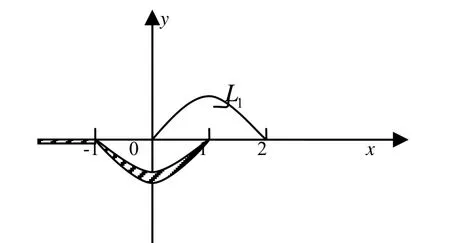
图1 w=Ln(1- z2)的可单值分支区域
2.3 w=)的可单值分支问题


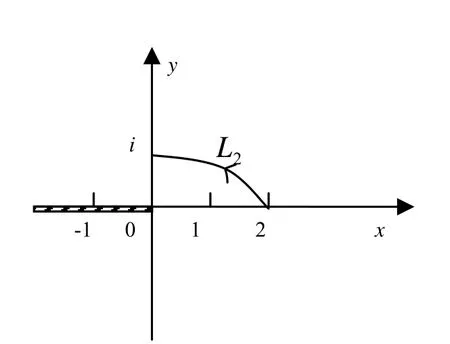
图2 w=的可单值分支区域
用连续变化法研究多值函数的单值分支问题时需要注意的是,支割线应尽量选取一条最简单的连接所有支点的曲线,特殊情况也可选多条,同时所作支割线要避开题中给出的已知点(起点)和要求的点(终点),因为这两点应该是在可单值分支区域内的,有时也在边界上岸或下岸;在可单值分支区域内作简单曲线连接起点和终点,因此这条简单曲线不能和支割线有交点.
容易看出和 Lnz分别是和 LnR(z)的特殊情况,也可用连续变化法求解,根据定理1和定理3,和 Lnz的支点都为 0,∞ ,因此任意一条连接0,∞的简单曲线都是支割线,但其中最简单的就是正实轴或负实轴,可见还是限制辐角法比较简单.
[1] 韩惠丽,房彦兵.多值函数在复变函数中的应用[J].大学数学,2007,23(4):180-183.
[2] 钟玉泉.复变函数论[M].北京:高等教育出版社,2004:64-87.
[3] 刘声华,宫子吉,沈永祥.初等解析函数[M].长春:吉林大学出版社,1991.
[4] 王长庆,姜俊彬.多值函数改变量及其在求解单值分支中的应用[J].辽宁师范大学学报,1997(4):347-350.
The Single-Valued Branches of Two Functions in Complex Number Field
FENG Zhi-xin
(College of Mathematics, Jilin Normal University, Siping, Jilin 136000, China)
In this paper, we make a systematic study of the single-valued branches of logarithmic function and radical function in complex number field by using “limiting argument” method and “continuous transforming” method.
multi-valued function; argument; function transforming; single-valued branches
O174.5
A
1673-2065(2012)01-0029-04
2011-09-26
吉林省教育厅“十二五”科学技术研究项目(2011- 160)
冯志新(1979-),女,吉林双辽人,吉林师范大学数学学院讲师,理学硕士.
(责任编校:李建明英文校对:吴秀兰)
