共形平坦流形中具有常平均曲率的超曲面

宋晴晴，宋卫东

（安徽师范大学数学计算机科学学院，安徽芜湖241000）

1 引言及主要结果

设Nn+1是n+1 维共形平坦单连通完备黎曼流形，Mn是Nn+1中具有常平均曲率的紧致无边的超曲面。对于共形平坦流形的子流形已有不少研究［1-3］。文［1］研究共形平坦黎曼流形中具有常平均曲率的完备超曲面，获得了一些刚性定理，文章继续类似的问题得到如下结果：

定理1设Mn是局部对称共形平坦流形Nn+1中的紧致无边的超曲面，且具有常平均曲率，以S代表其第二基本形式模长的平方，令Tc，tc分别是Nn+1的Ricci 曲率的上确界和下确界，如果Nn+1在Mn上x点处的截面曲率Kn+1in+1i满足，则

1）如果S≤，那么M是全脐的超曲面。

2）如果S=，那么M是全脐的或者与一个有两个不同的主曲率，且其中一个主曲率是一重的超曲面等距。

其中S代表其第二基本形式模长的平方，tc，Tc分别是Nn+1的Ricci 曲率的上确界和下确界，{λi}是M的主曲率。

2 准备工作

如无特别说明，规定各类指标的取值范围如下：

1 ≤A，B，C，…≤n+1;1 ≤i，j，k，…≤n

并且Σ 号下重复指标表示在相应范围内求和。

设Mn是n+1维局部对称共形平坦空间Nn+1中具有常平均曲率的完备超曲面。在Nn+1上选取局部标准正交标架场{eA} ，使得它限制在Mn上，{ei} 与Mn相切，en+1与Mn正交。设{ωA} 和{ωAB}分别是{eA} 的对偶标架场和联络1-形式。在此标架下Nn+1的结构方程为[4]

限制在Mn上，有[5]

其中：ωij是Mn的联络1-形式。hij，Rijkl，KABCD分别表示Mn的第二基本形式，曲率张量R的分量和Nn+1曲率张量K的分量。Mn的第二基本形式模长的平方的平均曲率。用hijk和hijkl分别表示hij的共变导数，则[5]

Nn+1是局部对称的，则

又Nn+1是共形平坦的，即其黎曼曲率张量为

其中：K，KAB分别为Nn+1的数量曲率、Ricci曲率。

令Tc，tc分别是Nn+1的Ricci曲率的上确界和下确界，则

引理[6]设u1，u2，…，un是n个实数，满足=B，B≥0，则

且等号成立当且仅当有n-1个ui相等。

3 定理1的证明

现定义hij的Laplacian为则

由于Mn具有常平均曲率，所以

因此

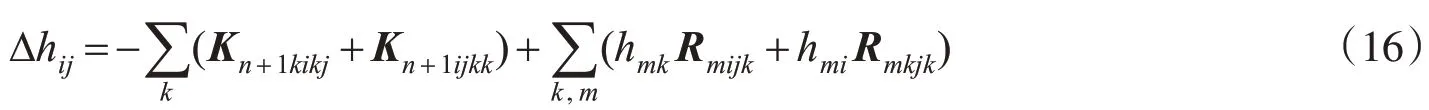
由［7］知

则有

选取适当的基使

下面估计（18）式中各项，由（11）式有

令

因此，由（13）（21）式有

作正交变换

F(x，y)可以写成

令x=，y=。

又由于（23）是正交变换，于是

x2+y2=u2+v2=S

可得

以（22）（24）得

由（18）（19）（20）（25）（26）式可得

又由定理1的条件可得

所以

1）若

则由（27）式有

0=|Z2|=S-nH2

于是M为全脐类空超曲面。

2）若

则（27）式等号成立，于是（22）（26）式均取等号，由（22）等号成立知，至少有n-1个λi相等。（i）若

λ1=λ2=…=λn

则M全脐。

（ii）若

λ1=λ，λ2=…=λn=u，λ≠u

利用hijk的定义。有

0=λiωij+λjωji=(λi-λj)ωij

故

从而当

当等式（22）成立时，有Kijij=。

由（6）式得

由引理不妨设

μ1=μ2=…=μn-1，μn≠μ1，μi=H-λi，i=1，2，…，n

故

λi≥H(i=1，2，…，n)

令

λ1=λ2=…=λn-1，μ=λn

由方程（30）可得

从而

所以，M与一个有两个不同的主曲率，且其中一个主曲率是一重的超曲面等距。

即定理1得证。

［1］吴泽九.共形平坦流形的一类具常平均曲率的完备超曲面［J］.华东交通大学学报，2008，25（2）：59-63.

［2］段仁杰，陈抚良. 局部对称共形平坦黎曼流形中具有平行平均曲率向量的紧致子流形［J］. 江西科学，2011，29（3）：308-312.

［3］宋卫东，刘敏.关于局部对称共形平坦空间中具有常数量曲率的子流形［J］.数学物理学报，2010，30（4）：1102-1110.

［4］ISHI HARA T. Maximal spacelike submanifolds of a pseudo-riemannian space of constant curvature［J］. Michigan Math J，1988，35（3）：345-352.

［5］YAU S T.Submanifolds with constant mean curvature I，II［J］.Amer J Math，1974，96（2）：346-366.

［6］OKUMURA M. Hypersurfaces and a pinching problem on the second fundamental tensor［J］.Amer J Math，1974，96（1）：207-213.

［7］水乃翔，吴国强.局部对称黎曼流形中的极小超曲面［J］.数学年刊，1995，16（6）：687-691.

［8］张剑峰.局部对称共形平坦黎曼流形中紧致子流形的一个刚性定理［J］.高校应用数学学报A辑，2002，17（4）：485-490.