一种基于反距离加权方法的层状三维地质界面拟合算法

李 楠，雷玲玲，肖克炎，

(1．中国地质科学院矿产资源研究所，北京 100037;2．长江大学地球科学学院，湖北 荆州434023)

一种基于反距离加权方法的层状三维地质界面拟合算法

李 楠1，雷玲玲2，肖克炎1，2

(1．中国地质科学院矿产资源研究所，北京 100037;2．长江大学地球科学学院，湖北 荆州434023)

三维空间中地质曲面模拟是矿产勘查、大比例尺成矿预测等地学领域的重要研究内容之一。与地球化学、地球物理数据的曲面拟合相比，地质界面拟合更加复杂且具有一般性。从功能需求角度出发，地质界面拟合需要处理层状地层、不整合地层以及存在构造的地层等多种情况;从算法实现角度讲，该拟合过程不同于物化探数据通过某一属性值进行曲面拟合的情况，因为在地质界面模拟过程中，不存在这样的特征值进行曲面拟合，因此不能直接使用物化探数据等值面提取的思想模拟地质接触界面。针对上述问题，提出了一种基于反距离加权法移动立方格算法的层状地层曲面拟合算法。该方法模型适合绝大多数层状地学三维曲面模拟。

地质界面;空间插值;移动立方格算法;等值面;隐式地质建模

0 引言

在地质勘探过程中，勘探人员通过钻孔、槽探、坑道、填图和编录等技术手段可以获取地质体和地质界面的三维控制点信息。在计算机领域，这些控制点被称为空间散乱点或离散点数据。由离散点集出发，重构该点集所属的曲面，称为曲面重建。笔者所讨论的地质界面重建属于该类问题。曲面重建，即构造出对象几何模型，是当今三维数据场建模的核心问题之一。曲面重建问题抽象为：给定三维空间曲面S上的一组采样点P，通过数学模型找到一个曲面 S'，使得 S'合理地逼近 S(Hoppe et al，1992)。其主要包括两大类算法：一类是参数曲面模型法，另一类是曲面提取法。

参数曲面模型法主要包括逼近样条曲面和插值样条曲面两种类型。其中，插值样条通过离散点，而逼近样条不过离散点。该方法的优点是曲面的获得不是由用户给定某一特征值得到的，而是由某一数学模型拟合得到的。但无论上述哪种方法，生成的地质界面均为单值面，不能很好地满足地质实际需要。文献对上述方法做了详细分析(毛先成，2006)。

曲面提取方法是地学曲面重构的主要研究内容。其核心思想是按照给定的阈值从体数据中抽取空间曲面，然后再按照传统方法进行绘制。这类方法主要包括轮廓线法(Keppel，1975)，等值面法(Lorensen et al，1987)，几何变换(Boissonnat，1984)等方法。提取等值面法由于其操作简单、精确度较高等原因一直是曲面重建研究的重要内容。这种方法的核心思想是用户给定一组值，算法根据这组值提取对应的等值面。

地质体接触界面提取与其他地学数据等值面提取的主要区别是接触界面提取的对象往往是一组地质认识信息而不是某一特征值，如，地球化学、地球物理等数据的分析值等。

综上所述，在上述两种曲面拟合算法思想的基础上，提出基于反距离加权方法和移动立方格(Marching Cubes，MC)算法的层状三维地质界面拟合算法。该算法的核心思想：首先由离散点进行空间插值得到三维栅格模型;其次建立增量函数f(Δ z)=zIDW－z，求出最优拟合曲面值 f(Δz)=ziso;最后，基于Marching Cubes算法和ziso追踪得到等值面S，即为层状地质界面。

1 算法思想

1．1 算法基本概念

介绍一些相关的概念及术语定义以便后文论述使用。

(1)曲面拟合(Edward，2003)。所谓曲面拟合，就是根据实际试验测试数据，求取函数f(x，y，z)与变量x，y，z之间的解析式，使其所确定的曲面通过或近似通过所有的实验测试点。也就是说，是所有实验测试点拟合的曲面M'能够合理逼近控制点所在曲面M。

(2)地理学第一定律(Tobler，1970)。任何事物之间均相关，而距离较近的事物总是比距离较远的事物影响更大。这里的距离不仅包含空间上的，也包含时间上的距离。

(3)移动立方格算法(Lorensen et al，1987)。移动立方格算法本质是从一个三维数据场中提取出一个等值面，所以也称为“等值面”算法。其算法思想是在规模大小为Nx×Ny×Nz的体数据场中，由每8个顶点组成1个体元，每个顶点都有1个数值，体元每条棱上的数值都是线性变化的。等值面的生成就是根据两相邻顶点的增量函数值生成等值点，然后将每个体元中的所有等值点按组合方式连接起来，生成指定值的等值面的过程。在标量场曲面的增量函数建立完成后，可以使用上述方法追踪地质体曲面。

(4)K-近邻查询。给定查询点和正整数K，从数据集中距离查询点最近的K个数据，当K=1时，为最近领域查询。

1．2 算法主要思想

笔者提出基于反距离加权方法和移动立方格算法的层状三维地质界面拟合算法。反距离加权方法假设未知点的值受较近控制点的影响比较远控制点影响更大。影响程度用点之间距离乘方的倒数表示。这种特性使得该方法可以应用于模拟连续曲面，最经典的例子是构建DTM模型。在三维空间中，尽管空间插值的结果是规则网格，但其数学本质不会发生变化，即较近控制点的影响比较远控制点影响更大。因此，如果待插值为高程值z，则空间插值的结果表示由采样点拟合的曲面M。此时就可以使用移动立方格算法提取曲面M'，使之能够合理逼近控制点所在曲面M。

1．3 算法流程

如1．2节所述，总结笔者提出的算法总体流程如下。

步骤1：基于反距离加权(IDW)方法对地层采样点的高程值z进行空间插值。

步骤2：建立插值结果与待插点实际高程值z'的增量函数f(Δz)。

步骤3：选择增量函数f(Δz)的某个值，作为曲面提取值。

步骤4：应用移动立方格(MC)法，提取f(Δz)的某个值处的等值面。

步骤5：计算曲面光照、设置颜色、重建曲面拓扑结构等。

综上所述，根据算法的主要思想和总体流程，总结算法流程如图1所示。

图1 算法总体流程图

2 算法实现

本算法主要包含两个主要内容：(1)快速三维空间插值算法;(2)移动立方格算法。

在三维空间中，随着点数量的增加，K-近邻查询非常耗时。例如，在三维空间中对12 000个点进行反距离加权空间插值，设待插点达到1 000万，如果使用线性方法进行方法其时间复杂度将达到0(12 000×10 000 000)。可以看出，上述方法的时间复杂度是用户无法接受的。

笔者提出使用八叉树和R-Tree树两种空间索引结构，完成三维散乱点云的K-近邻查询，提高三维空间插值算法的效率。

2．1 算法1：三维离散点快速空间插值算法

输入：离散点集合 P{(x，y，z)|x，y，z为任意实数}

输出：栅格体S

步骤1：建立三维点云P的八叉树空间索引。步骤2：建立八叉树空间索引的三维R-Tree树索引。

步骤3：通过矩阵计算获得待插点的搜索范围。

步骤4：应用反距离加权方法对地层分界点的高程值z进行空间插值，得到S。

使用移动立方格算法，提取地质曲面。

在移动立方格方法中，由于每个体元存在8个顶点，每个顶点可能有正和负两种状态(等值面经过0状态)，因此，每个体元按照其顶点的正、负分布，共有28=256种不同的组合状态。尽管判断等值面将与哪些体元相交在理论上很容易理解，但是，根据这256种状态求出每个体元的等值面是个相当繁琐且容易出错的过程。实际工作中，根据互补对称性和旋转对称性可以将这256种状态简化为15种情况(蒋先刚，2003)(图2)。但是，简化的模型是一个存在二义性的模型，在文中采用渐近判别法(Nielson et al，1991)来消除二义性。

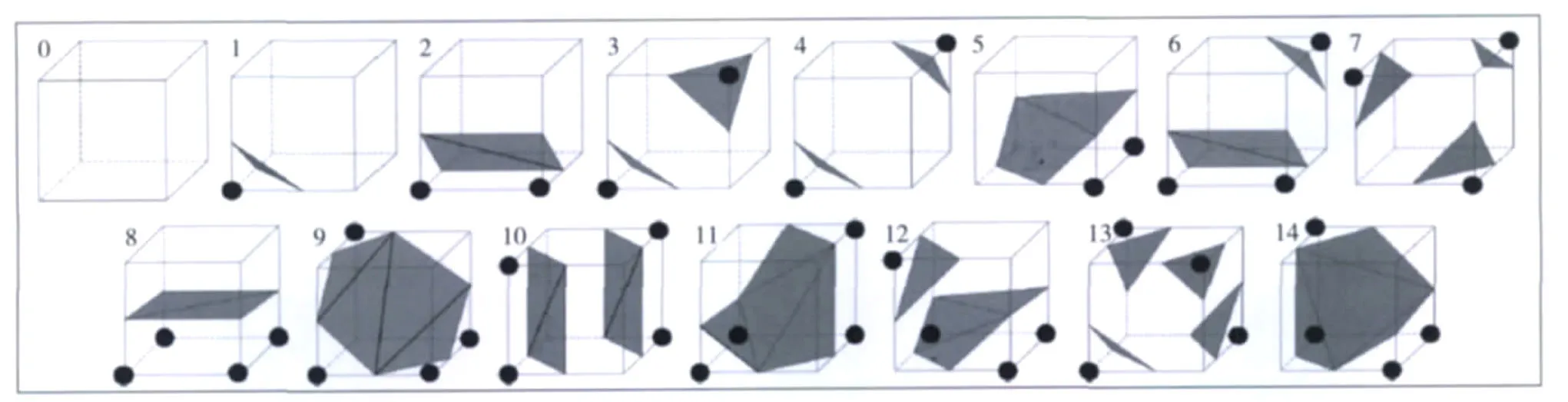
图2 模型简化的15种情况

2．2 算法2：提取地质分界曲面

输入：栅格体S，待提取等值面的值ziso

输出：三角网Surface

步骤1：查找包含值ziso的立方格。

步骤2：按照图2的方式生成三角面片。

步骤3：计算每一个三角形的法向量。

步骤4：结束。

3 实验与分析

使用西藏某矿区三维地层采样数据作为实验数据，该矿区由钻孔获得的地层分界界面采样数据是416个。实验环境、硬件开发环境：CPU主频为2.16G Hz和内存为1G的PC机;软件开发环境：MS Windows XP操作系统和Visual C++7．0。算法效果如图3、图4、图 5、图 6、图7 所示。

4 结论

在已有曲面拟合算法思想的基础上，笔者提出了基于反距离加权方法和移动立方格算法的层状三维地质曲面拟合算法。本算法的优点在于以数学原理与地理学第一定律为基础，实现层状地层的快速、精确拟合。该方法模型能够适合绝大多数层状地学三维曲面模拟。不足之处是不能解决不整合、构造等复杂情况，这也是本算法下一步研究的方向。

图3 地层接触界面采样点

图4 栅格化结果

图5 地层分界界面拟合结果

图6 地层分界界面拟合与剖切结果对比

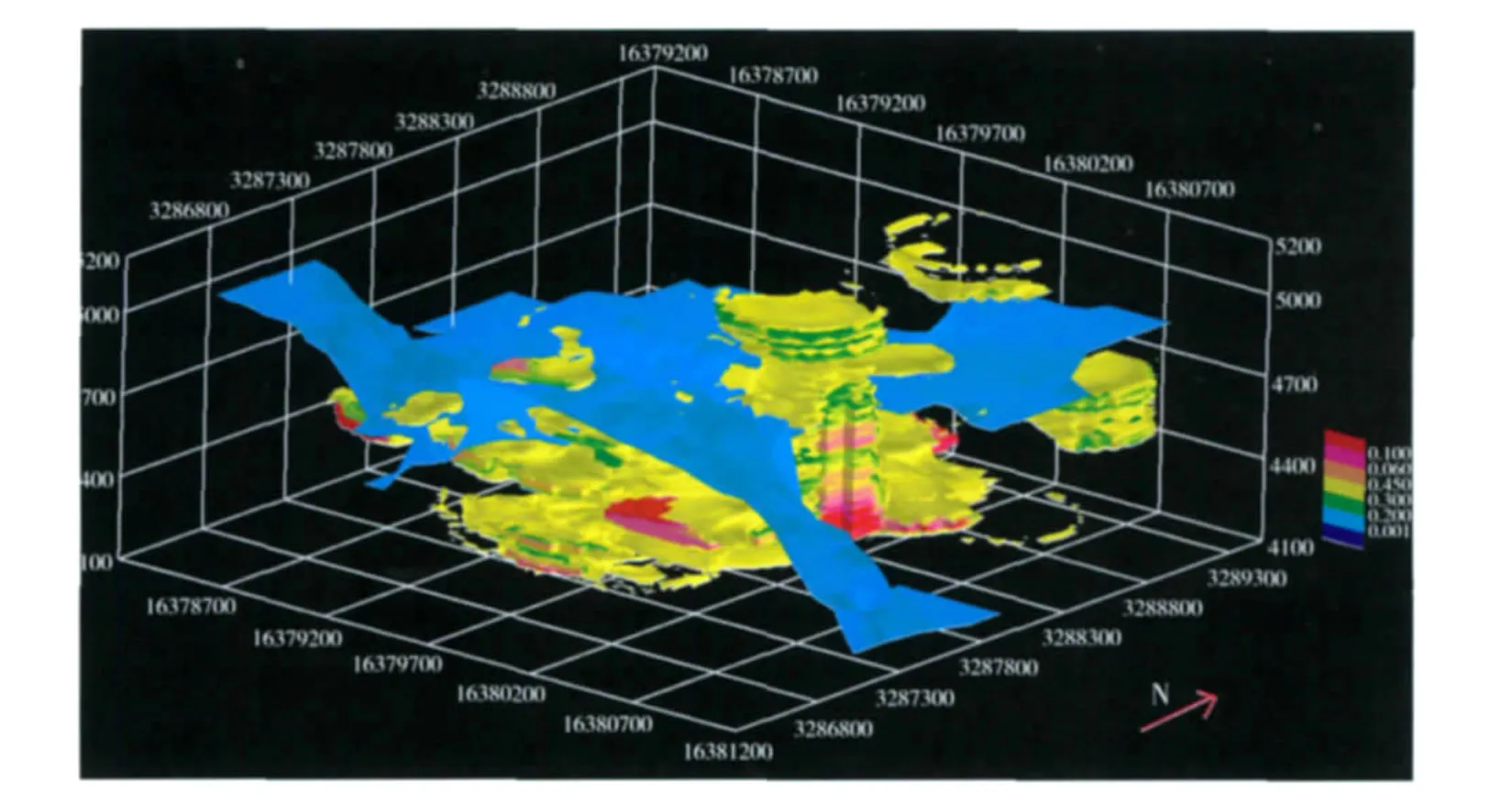
图7 地质界面与化探异常以及矿体复合显示

毛先成．2006．三维数字矿床与隐伏矿体立体定量预测研究［D］．长沙：中南大学．

蒋先刚．2003．三维数据场重构与显示工程软件设计［M］．北京：万水出版社．

BOISSONNAT J D．1984．Geometric structures for three-dimensional shape represent ation［J］．ACM Trans Graphics，3(4)：266－286．

EDWARD ANGLE．2003．Interactive Computer Graphics：A Top-Down Approach Using OpenGL［M］．Beijing：Higher Education Press．

HOPPE H，DEROSE T，DUCHAMP T，et al．1992．Surface reconstruction from unorganized points［J］．Computer Graphics，26(2)：71－78

KEPPEL E．1975．Approximating complex surfaces by triangulation of contour lines［J］．IBM Journal of Research and Development，19(1)：2 －11．

LORENSEN W E，CLINE H E．1987．Marching Cubes：A high Resolution 3D Surface Construction Algorithm ［J］．Computer Graphics，21(4)：163 －169．

NIELSON G M，HAMANN B．1991．The asymptotic decider：resolving the ambiguity in marching cubes［C］//Proceedings of Visulization'91，San Diego：CA，83－91．

TOBLER W．1970．A computer movie simulating urban growth in the Detroit region［J］．Economic Geography，46(2)：234－240．

Stratiform 3D geological interface fitting algorithm based on inverse distance weighted method

LI Nan1，LEI Ling-ling2，XIAO Ke-yan1，2

(1．Institute of Mineral Resources，Chinese Academy of Geological Sciences，Beijing 100037，China;2．School of Geosciences，Yangtze University，Jingzhou 434023，Hubei)

Geological curved surface modeling was an important research content in fields of mineral exploration and large-scale mineral assessment．Geological curved surface modeling was more complex，and of generality compared with that of other geological data like geochemical data or geophysical data．Geological curved surface modeling needed to solve many complex situations such as unconformity or faults．In response to these issues，the authors proposed an algorithm of fitting layered geological surface that was based on two algorithms of inverse distance weighted method(IDW)and marching cubes(MC)．The algorithms were characteristic of speedy，accurate fitting for stratified layers on the foundations of mathematical principles and the first theorem of geography，suited most 3D curved surface modeling of the layered earth sciences．

Geological interface;Spatial interpolation;Marching cubes algorithm;Iso-surface;Implicit geological modeling

TP391

A

1674－3636(2012)03－0291－05

10．3969/j．issn．1674-3636．2012．03．291

2012－06－06;编辑：陆李萍

国家高技术研究发展计划(863)“矿产资源评价数字矿床模型及可视化技术研究”(2006AA06Z114)、国家科技支撑计划“西部优势矿产资源潜力评价技术及应用研究”(2006BAB01A01)、矿产勘查三维预测评价信息平台开发及应用示范研究(1212010012013)、中央国家机关基本业务费基金项目等基金资助

李楠(1980— )，男，副研究员，博士，主要从事地图制图与地理信息工程、大比例尺矿产资源评价研究，E-mail：superln1980@yahoo．com．cn