新的格子Bhatnagar-Gross-Krook模型求解修正的Burgers方程
2012-12-19乐励华
高 云, 乐励华
(东华理工大学数学与信息科学学院,江西抚州 344000)
新的格子Bhatnagar-Gross-Krook模型求解修正的Burgers方程
高 云, 乐励华
(东华理工大学数学与信息科学学院,江西抚州 344000)
随着计算机技术的发展,数值模拟方法求解偏微分方程得到越来越广泛的应用。格子Boltzmann方法是一种新型的模拟方法,由于该方法具有计算效率高、边界条件容易处理、完全并行性等独特的优点,使得它具有广泛的应用领域。利用格子Bhatnagar-Gross-Krook模型来求解修正的Burgers方程,首先用该方法正确的恢复了宏观方程,然后数值模拟了两个具有解析解的修正Burgers方程。把模拟解与解析解进行对比,发现数值解与解析解和前人研究中的数值解都吻合很好。
格子BGK模型;修正的burgers方程;数值解
高云,乐励华.2012.新的格子Bhatnagar-Gross-Krook模型求解修正的Burgers方程[J].东华理工大学学报:自然科学版,35(1):89-93.
GaoYun,Le Li-hua.2012.A New Lattice Bhatnagar-Gross-Krook Model for the Modified Burgers’Equation[J].Journal of East China Institute of Technology(Natural Science Edition),35(1):89-93.
本研究考虑的修正burgers方程为
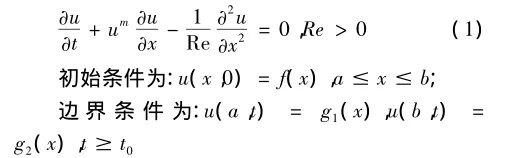
其中Re是描述粘性系数v(=1/Re)的Reynolds数。
修正的burgers方程是重要的非线性对流扩散方程。Bateman(1915)第一次提出burgers方程,之后,很多学者作了进一步的研究和发展。近年来,修正的burgers方程被应用于实际的输运问题中,例如湍流、波在热弹性介质中的传播、河流和沉淀物中污染物的运输和散射、低频吸收的媒介中非线性波的传播等。许多学者一直在构造修正burgers方程的高效数值方法。Irk(2009)采用六次样条函数的配置方法、Bratsos(2010)用有限差分方法、Ramadan(2005a)采用五次样条插值的配置方法来求解修正burgers方程。
格子Boltzmann方法在模拟流体复杂的物理问题时是一种有效的方法。与传统的计算方法相比,该方法具有许多独特的优势,如计算效率高、边界条件容易处理、具有完全并行性等。格子Bhatnagar-Gross-Krook(BGK)模型是目前格子Boltzmann方法研究和应用的主要模型之一,已经在多孔介质流(Xu et al.,2004)、血液流(Fang et al.,2004)、多相流(Hou,1997)等领域取得了很大的成功。由于格子Boltzmann方法的独特优势,目前,该方法正逐步应用于模拟非线性系统,如对流扩散方程(Shi et al.,2009,2010),反应扩散方程(Chen et al.,1995),泊松方程(Chai et al.,2008),KdV方程(Chai et al.,2008)等。
本文在基于格子BGK模型和Chapman-Enskog展开的基础上来求解方程(1),发现数值解与解析解和其它模型的数值解都吻合很好。
1 格子BGK模型
使用Qian等(1992)提出的D1Q3模型,该格子BGK模型分布函数的演化方程为:
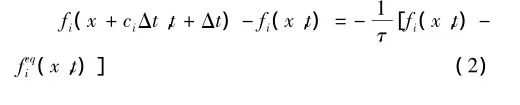



尽管,阎广武等(1999)应用多尺度展开技术,通过选择平衡态分布函数的高阶矩的格子Boltzmann方法研究了Burgers’方程,对于一维模型,将速度离散成4个方向,每一个节点与相邻近的4个节点相连,即D1Q4模型。Duan等(2008)针对该方程提出2-bit模型,即D1Q2模型,将速度离散成2个方向,每一个节点与相邻近的2个节点相连,通过Taylor展开和多尺度分析,从格子Boltzmann方程恢复了Burgers’方程。但是,对于Burgers’方程本研究选取D1Q3模型,介于即D1Q4模型与D1Q2模型之间,本研究模型更简单,精度也更高。
2 数值模拟
为了验证D1Q3格子BGK模型的有效性,模拟了修正 Burgers方程。在模拟中,使用了 Guo等(2002)提出的非平衡态外推方法来处理边界条件。为了检验数值方法的有效性,误差定义为:


在模拟中,选取 α=0.9,Δx=0.005,Δt=0.01。表1给出数值模拟结果与解析解的比较,从中可以看出数值解与解析解和 Ramadand等(2005b)模拟的解差别很小。表2显示了误差的比较,可以看出本文的误差较小。表3给出了不同粘性系数v的误差,v越小的,误差越小。因此,格子BGK模型更适合小的粘性系数v。另外,还模拟了v=0.001和v=0.000 5两种情况(图1,图2),从图中可以看出数值解和解析解非常吻合。

表1 数值解与解析解的比较在v=0.001,t=4.0Table 1 Comparison of numerical solution and analytic solution while v=0.001,t=4.0
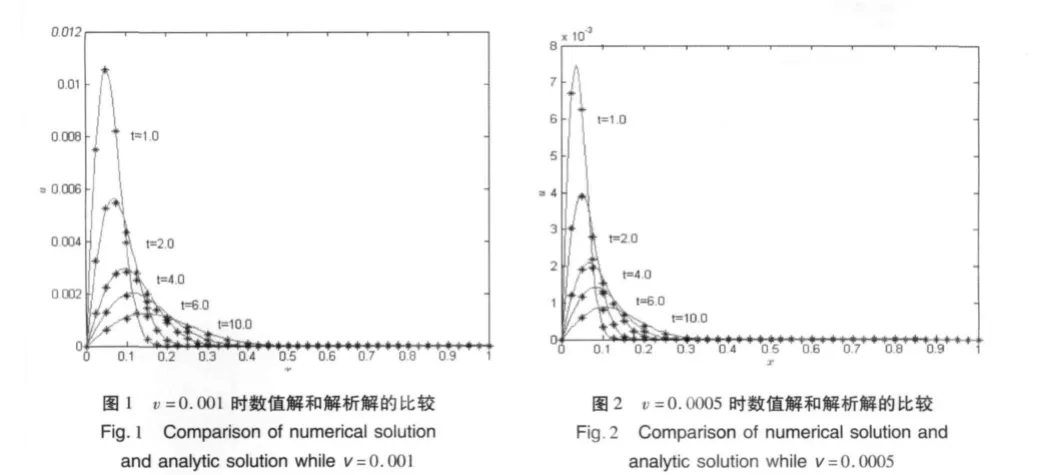
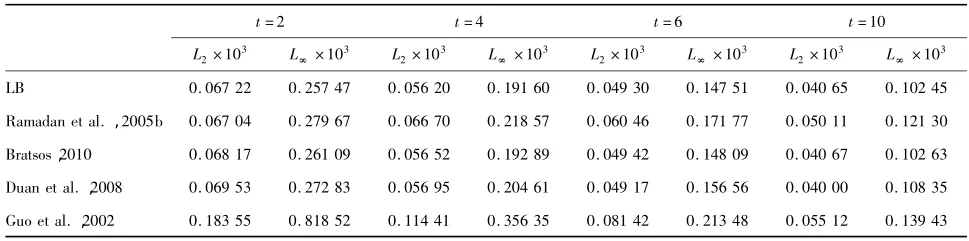
表2 v=0.001,Δx=0.005,Δt=0.01时误差比较Table 2 Error comparison while v=0.001,Δx=0.005,Δt=0.01

表3 不同粘性系数v的误差比较Table 3 Error comparison of different v of viscosity coefficient

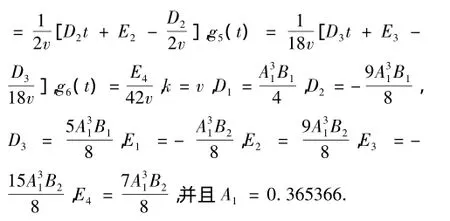
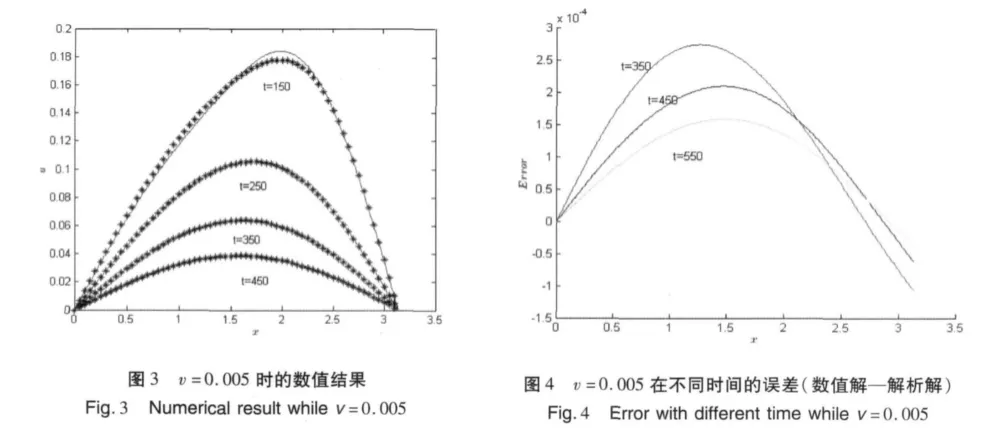
选取Δx=0.01,Δt=0.01,α=0.1,v=0.005进行模拟。然后将所得的数值结果与其它文献结果进行L2,L∞误差比较(表4)。发现格子BGK模型的误差更小。图3显示了粘性系数时的数值结果。图4显示了数值解与解析解的误差情况。

表4 v=0.004在不同时间的误差比较Table 4 Error comparison with different time while v=0.004
4 结语
本研究在基于格子BGK模型的基础上,对修正的Burgers方程进行了数值模拟。发现本文模拟的数值结果和方程的解析解吻合很好。由于采用D1Q3模型,将速度离散成3个方向,每一个节点与相邻近的3个节点相连,简化了算法的同时,也减少了误差。同时,也与以前文献的结果也进行了比较,发现本研究的误差更小。对模型稳定性分析是下一步工作的目标。
阎广武.1999.用格子Boltzmann方法研究Burgers方程[J],力学学报,31:143-151.
Bateman H.1915.Some recent researches on the motion of fluids[J].Monthly Weather Rev,43:163-170.
Bratsos A G.2010.A fourth-order numerical scheme for solving the modified Burgers equation[J].Comput.Math.Appl 60:1393-1400.
Bratsos A G,Petrakis L A.2011.An explicit numerical scheme for the modified Burgers’equation[J].Int.J.Numer.Meth.Biomed.Engng 27:232-237.
Chai Z H,Shi B C,Zheng L.2008.A unified lattice Boltzmann model for some nonlinear partial differential equations[J].Chaos Solitons Fractals,36:874-882
Chai Z H,Shi B C.2008.A novel lattice Boltzmann model for the Poisson equation[J].Appl.Math.Model 32:2050-2058.
Chen S,Dawson S P,Doolen G D,et al.1995.Lattice methods and their applications to reacting systems[J].Comput.Chem.Eng.,19:617-646.
Duan Y L,Liu R X,Jiang Y Q,2008.Lattice Boltzmann model for the modified Burgers’equation,Appl.Math.Comput 202:489-497.
Fang H P,Chen S Y.2004.Boltzmann method for three-dimensional moving particles in a Newtonian fluid[J].Chin.Phys.,13:47-53.
Guo Z L,Zheng C G,Shi B C.2002.Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J].Chin.Phys.,11:366-374.
Hou S,Shan X,Zou Q,et al.1997.Evaluation of two lattice Boltzmann models for multiphase flows[J].J.Comput.Phys.,138:695-713.
Irk D.2009.Sextic B-spline collocation method for the modified Burgers equation[J].Kybernetes,38:1599-1620.
Qian Y,d’Humiéres D,Lallemand P.1992.Lattice BGK models for Navier-Stokes equation[J].Europhysics Letters.,17:479-484.
Ramadan M A,El-Danaf T S.2005a.Numerical treatment for the modified Burgers equation[J],Math.Comput.Simul,70:90-98.
Ramadan M A,El-Danaf T S,Alaal F.2005b.A numerical solution of the Burgers’equation using septic B-splines[J].Chaos Solitons Fractals,26:1249-1258.
Saka B,Da 2008.A numerical study of the Burgers’equation[J].J.Franklin Inst 345:328-348.
Shi B C,Guo Z L.2009.Lattice Boltzmann model for nonlinear convection-diffusion equations[J].Phys.Rev.E,79:016701.
Shi B C,Guo Z L.2011.Lattice Boltzmann simulation of some nonlinear convection-diffusion equations[J].Comput.Math.Appl.,61:3443-3452.
Xu Y S,Zhong Y J,Huang G X.2004.Lattice Boltzmann method for diffusion-reaction-transport processes in heterogeneous porous media[J].Chin.Phys.Lett.,21:1298-1301.
A New Lattice Bhatnagar-Gross-Krook Model for the Modified Burgers’Equation
GAO Yun, LE Li-hua
(Dept.of Mathematics&Information Science,East China Institute of Technology,Fuzhou,JX 344000,China)
The methods of numerical simulation are applied widely with the development of computer technology.The lattice Boltzmann method has a more wide application owing to its high computing efficiency,easier processed boundary conditions,and parallel computation.In this study,the Bhatnagar-Gross-Krook model is used to solve the modified Burgers’equation.First,the macroscopic equation is recovered with this model.Then,the two modified Burgers’equations with analytical solutions are numerical simulated.Results show numerical simulation and analytical solutions match well with numerical simulation of previous publication.
LBGK model;modified burgers’equation;numerical solution
O24
A
1674-3504(2012)01-089-05
10.3969/j.issn.1674-3504.2012.01.013
2011-09-18 责任编辑:张国庆
高 云(1986—),女,硕士生,研究方向:微分方程。E-mail:gaoyun1986@126.com
