干污泥表面形貌及孔隙分布规律*
2012-12-18张忠梅孙春华金孝祥赵培涛葛仕福刘长燕
张忠梅 孙春华 楼 军 金孝祥 赵培涛葛仕福 刘长燕
(1.浙江富春江环保热电股份有限公司 2.东南大学能源与环境学院)
干污泥表面形貌及孔隙分布规律*
张忠梅**1孙春华1楼 军1金孝祥1赵培涛2葛仕福2刘长燕2
(1.浙江富春江环保热电股份有限公司 2.东南大学能源与环境学院)
污泥干燥焚烧以回收其热能的资源化利用正受到越来越多的关注。污泥干燥过程中,孔隙的大小及其分布直接影响污泥中液体及气体的传递过程,进而影响干燥速率。为研究干污泥表面形貌及孔隙分布规律,采用扫描电子显微镜观测了干污泥表面形貌,利用动态氮吸附法测量了干污泥的孔隙大小。利用数理统计方法研究了孔隙分布规律,研究结果表明干污泥的孔隙分布服从对数正态分布。建立了孔隙分布模型,求解了5种干污泥的孔隙分布特征参数,模型计算值与实际测量值吻合较好,均方根误差小于18.2%,所建立的干污泥孔隙分布模型具有一定的通用性及准确性。
干燥 干污泥 表面形貌 孔隙分布规律
0 前言
污泥是污水处理的副产品,不仅产量大,而且成分极其复杂,若处理不当,会造成二次污染。同时,作为二次资源,其资源化利用已经成为当今国内外广泛关注的课题之一。无论是热能利用,制复合肥,还是用作建材或其它化工原料,减少含水率是关键,污泥干燥或半干燥成为污泥资源化利用的第一步[1]。绝大多数干污泥是多孔物料,研究多孔物料干燥机理常采用的Whitaker宏观控制方程[2],实际上是一种体积平均意义上的近似,它把实际过程的复杂性转化到某些未知参数 (如有效扩散系数、有效导热系数等)上,这些参数无法直接测定。将多孔物料作为各向同性的介质来建立多相流传热传质方程,本身存在一定的缺陷。事实上多孔物料固相具有一定的框架,绝不是各向同性,水分扩散必然会受框架的影响而改变大小及方向。因此,孔隙的大小及其分布规律是多孔物料的重要结构特征,它直接影响多孔物料中液体及气体的传递过程[3-6]。通过对干污泥的形貌及孔隙分布展开研究,可以了解污泥干燥过程中的相关传递特性。
国内外在冶金、陶瓷、塑料、催化剂等多孔材料的孔径测量方法及孔隙分布规律等方面进行了较多的研究。对材料孔径及其分布的测定方法主要有:断面直接观测法、气泡法、透过法、气体吸附法、压汞法、X射线和中子的小角度散射等[7-10]。但干污泥的孔隙采用何种方法测量没有见过报道,对其孔隙分布规律的研究也较少。本文采用扫描电子显微镜对干污泥表面形貌进行观察实验,利用动态氮吸附法测量其孔隙大小,研究其分布规律,探究干污泥形态特征对干燥过程的影响,为污泥的资源化处理提供理论指导。
1 干污泥表面形貌实验观察
1.1 被测样品
污泥取自不同污水处理厂的脱水间,采用惰性粒子流化床干燥后,再在80℃真空下烘干数小时,得到本文的研究样品。不同样品的来源及性质如表1所示。

表1 污泥样品的来源及性质
1.2 观察结果
采用Sirion 200型扫描电子显微镜 (scanning elactren microscope)对被测样品表面形貌进行观察实验,其分辨率为1.5 nm,放大倍率为20万~30万倍。
图1、图2分别示出了样品1、样品5干燥后的形貌放大图。可以看出:在放大倍数较小时,孔隙分布不明显;但当放大倍数较大时,可以清楚地发现,干污泥是由大小不等的孔隙构成的多孔介质。

图1 印染污泥干品 (样品1)放大形貌

图2 造纸污泥干品 (样品5)放大形貌
2 干污泥孔隙半径的测量
2.1 测试方法和仪器
为了保证测量精度,对于不同的孔径范围应采用不同的测量方法。在干燥过程中,可将物料中的孔隙通道视为当量毛细管,其大小可用当量毛细管半径r来表示。毛细管中润湿壁面的液体与汽(气)体之间的界面呈下弯的凹液面形,此弯曲液面上的饱和蒸汽压pv与平液面上的饱和蒸汽压ps是不相同的。Kelvin定律将弯曲液面上的蒸汽分压pv与平液面上的饱和蒸汽压ps的关系表示成下式:
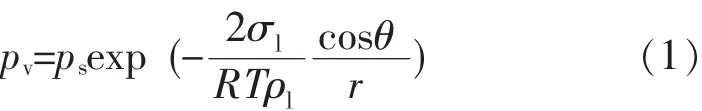
式中,σl、R、ρl、T分别为表面张力、气体常数、液体密度和温度。对于水和水蒸气,标准状态下其值 分 别 为 0.073 1 N/m、 461.5 J/(kg·K)、 998.2 kg/m3、 293 K。
假设液态水在毛细管中保持完全润湿状态,即润湿角θ=0,则在标准状态下式 (1)可写成:

从式(2)可知:当 r=1×10-7m 时, φ=0.99, 说明孔隙中水液面蒸汽分压pv与平液面上的饱和蒸汽压ps基本相同。以r=10-7m为界,可将毛细管分为微毛细管 (r<10-7m)和大毛细管 (r>10-7m)。对于污泥干燥过程,影响内部传递特性的主要是微毛细管,该范围孔径的测量通常采用灵敏度高、技术先进的动态氮吸附法测定。
本文采用动态氮吸附测量仪测量干污泥的孔隙半径,所用的氮气压力比pv/ps调节范围为0.05~0.98,控制精度达99.9%,氮、氦气体的纯度大于99.99%,测试精度高、重现性好,重复性误差小于3%。
2.2 干污泥孔隙半径的测量结果
采用动态氮吸附法对表1中5种样品的孔隙半径进行了测量,图3示出了样品1的孔隙分布曲线。由图3可见,在线性坐标系中,孔隙大小分布为非线性关系。为研究孔隙分布特征,应在非线性坐标系中研究孔隙分布规律。
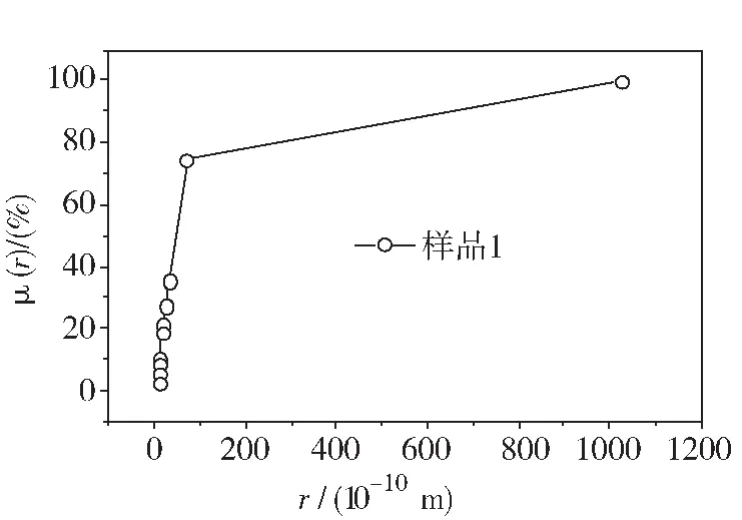
图3 样品1的孔隙分布曲线
3 干污泥孔隙分布规律
为了寻找孔隙分布规律,将样品1(见图3)及其它样品的孔隙分布曲线分别作在不同的坐标系中,结果发现,在对数正态坐标系中,孔隙分布函数与孔隙直径呈线性关系,如图4所示。在对数正态坐标系中,对5种样品的孔隙分布进行线性回归,求取每种样品的相关统计参数,结果如表2所示。可以看出,5种样品中,线性相关系数R2最小的是样品4,为0.946,其余样品的线性相关系数R2均大于0.987,说明这几种干污泥的孔隙分布基本上都服从对数正态分布,这与其他研究者对土壤、脱硫剂孔隙分布的研究结果一致[11-16]。
为了获得孔隙分布的数学表达式,假设干污泥的孔隙的半径分布是连续的,孔的形状为圆柱形,且孔隙分布函数f(r)具有对数正态分布形式,为:

图4 对数正态坐标系中干污泥样品的孔隙分布

表2 线性回归结果

式中,μ为孔隙分布函数的均值,代表了孔隙半径的取值中心;σ为孔隙分布函数的方差,代表了孔隙半径r的可能取值与均值μ的偏差的疏密程度。
模型方程 (4)中的均值μ、方差σ与对数正态坐标系中回归的直线斜率K、截距B的关系为:

将表2中的线性回归结果代入式(5)及式(6),即可求得各样品孔隙分布函数的特征参数。
根据上述方法,求得各样品孔隙分布特征参数如表3所示。可以看出:5种样品的孔隙均值在2~4.5 nm之间,属于微孔范围。一般来讲,均值μ大的多孔物料,其平均孔隙半径大,内部扩散阻力小,且降速干燥的传质势 (即毛细管中液面蒸汽分压pv)大,所以降速干燥速率大,降速干燥时间短;方差σ小的多孔物料,孔隙半径集中在均值μ附近,特别小的孔隙所占份额少,降速干燥时间短。5个样品中,样品1的均值最大且方差最小,相同条件下,降速干燥速率最大,干燥处理最容易;样品4的均值最小且方差最大,干燥处理最困难。

表3 干污泥孔隙分布函数的σ、μ值
将表3中的方差σ和平均值μ代入式 (4),可求解不同孔隙直径下的累计孔隙率Φ (r)。将计算值Φ (r)与实际测得的孔隙半径r所对应的孔隙率相比较,如图5所示。5种样品中,实际测量值与理论计算值相比,最大标准误差仅为18.2%,其中的3种小于9%,可见理论预测值与实际测量值吻合度较好,文中建立的干污泥孔隙分布模型具有一定的通用性和准确性。

图5 几种干污泥孔径分布的测量值与理论值的比较
4 结论
(1)采用扫描电子显微镜对干污泥表面形貌进行观察,得到了印染污泥及造纸污泥干燥后的形貌放大图,发现干污泥是由大小不等的孔隙构成的多孔介质。
(2)采用动态氮吸附法测量了5种干污泥的孔隙半径,结果表明5种污泥样品的孔隙均值为2~4.5 nm,属于微孔范围。
(3)干污泥的孔隙分布基本服从对数正态分布,建立了孔隙分布数学模型,求解了5种干污泥的孔隙分布特征参数。
(4)比较了模型方程的计算值与实际测量值,两者均方根误差最大仅为18.2%,两者吻合度较好,所建立的干污泥孔隙分布模型具有一定的通用性和准确性。
[1]解光武,蔡明招,郑文芝.国内外污泥的处理与处置技术 [J].环境技术,2003(5):24-27.
[2]Whitaker S.Simultaneous heat,mass and momentum transfer in porous media:A theory of drying[J].Advances in Heat Transfer,1977,13:119-203.
[3]李爱民,曲艳丽,杨子贤,等.污水污泥干燥过程中表观形态变化及水分析出特性 [J].化工学报,2004,55(6):1011-1015.
[4]李爱民,曲艳丽,陈满堂,等.污水污泥干燥特性的实验研究 [J].燃烧科学与技术,2003,9(5):404-408.
[5]葛仕福,施明恒.颗粒表面料层干燥机理 [J].化工学报,2005,56(1):30-34.
[6]安丽,陈祖齐,潘智生,等.污泥处置方法的研究[J].环境工程,2000,18(1):40-43.
[7]丁祥金,张继周,宝志琴,等.泡点法测定微孔径分布的改进算法[J].无机材料学报,2000,15(3):493-498.
[8]谭罗荣.岩土材料孔径分布测试结果的修正 [J].岩土力学,2002,23(3):263-267.
[9]刘培生.多孔材料孔径及孔径分布的测定方法 [J].钛工业进展,2006,23(2):29-34.
[10]朱黎冉,魏芸,李忠全.气泡法测量多孔材料孔径分布 [J].粉末冶金工业,2006,16(4):26-30.
[11]Feike J Leij,Teamrat A Ghezzehei,Dani Or.Modelling the dynamics of the soil pore-size distribution[J].Soil&Tillage Research,2002(64):61-78
[12]贾力,刘立平.CaO孔隙形成与钙转化的实验研究[J].工程热物理学报,2005,26(4):680-682.
[13]Mahuli S K,Agninotri R,Shriniwas C.Pore structure optimization of calcium carbonate for enhanced sulfation[J].American Institute of Chemical Engineers,1997,43(9):2323-2335.
[14]Simons G A,Garman A R.Small pore closure and the reaction of the limestone sulfation reaction[J].American Institute of Chemical Engineers,1986,32(9):1491-1499.
[15]曾艳艳,贾力.氧化钙孔结构特征的数学描述与分析[J].北京交通大学学报,2006,30(1):107-110.
[16]葛仕福,施明恒.被干燥多孔物料中孔隙大小及分布的探讨 [J].应用科学学报,2005,23(1):94-98.
Surface Morphology and Pore Size Distribution of Dried Sludge
Zhang Zhongmei Sun Chunhua Lou Jun Jin Xiaoxiang Zhao Peitao Ge Shifu Liu Changyan
Sludge drying and incineration for energy recovering has
more and more attention in recent years.The size and distribution of pores directly affect the transfer properties of liquid and gas in the sludge during drying process.In this paper,SEM (scanning electron microscope)was employed to observe the surface morphology and the Dynamic-Nitrogen-Adsorption method was used to measure pore size of the dried sludge.Then the data was analyzed with mathematical statistics.The results showed that the pore distribution of dried sludge obeyed the lognormal distribution.A theoretical model was built to solve the pore distribution parameters of five kinds of dried sludges.The root mean square error was less than 18.2%,implying a good agreement was reached between the experimental data and the theoretical calculating values.It also indicated that the model proposed in this study was accurate and practicable.
Drying;Dried sludge;Surface morphology;Pore distribution
TQ 028.6
水体污染控制与治理科技重大专项 (2010ZX07319-002)。
**张忠梅,男,1962年生,工程师。富阳市,311418。
2012-08-03)
