Zoomfft算法的实现

华北电力大学电气与电子工程学院 王 涛 陈邵权 范寒柏 王 磊

1.引言

传统的FFT方法得到的信号频谱是一种离散的频谱，其分辨率为Δf=fs/N，其中，fs为采样频率，N为采样点数。由此我们可以得出，频谱的分辨率是由采样频率fs和采样点数N来确定，根据乃奎斯特采样定理，要使信号的频谱不产生混叠，采样频率fs应大于信号带宽的两倍。而分辨率的提高(Δf越小分辨率越高)只能通过降低采样频率fs或增大采样点数N，但fs的降低受到乃奎斯特定律的限制，不能过小，过小会发生频谱混叠；而增加取样点数会增加运算量和存储量，使得算法的时间增大，效率降低。由此看来,只有长的时间数据才有可能得到高的频率分辨力,但是由于实际测量条件和硬件方面等的限制,这样做并不总是可能的。而在实际测量中，我们往往只是对信号的某一频段的频率感兴趣，只分析这个频段的信号即可。基于复调制的ZOOMFFT可以实现在较窄的频带范围实现较高的频率分辨率。是一种折中的方法[4]。因此在很多领域得到了广泛的应用。

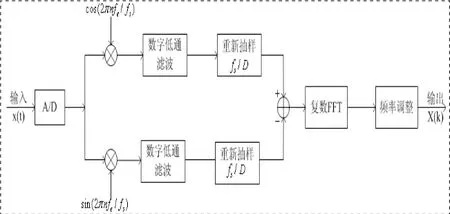
图1 基于复调制ZoomFFT的基本原理流程图

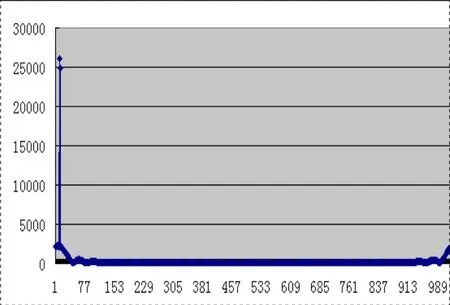
图2 实际信号ZoomFFT后未进行频率调整的频谱

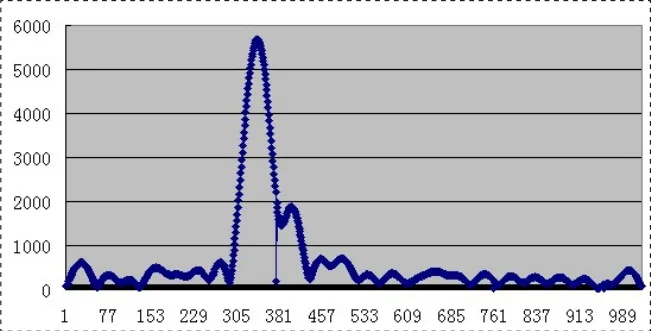
图3 测量物体动态时得到的频谱

2.ZoomFFT的基本原理

ZoomFFT方法基本原理是：移频——数字低通滤波——重新抽样——复FFT——频率调整，其原理过程如图1所示。

设模拟信号为x(t)，经过A/D采样后，得到离散的序列x0(n)，(n=0,1…N-1)，fs为采样频率，fe为需要细化频带的中心频率，D为细化倍数，N为FFT的点数，X(k)为输出的序列。具体的算法过程可归纳为以下几个步骤：

(1)复调制移频

所谓复调制移频指的是将频域坐标向左或向右移动，使得被观察的频段的起点移动到频域坐标的零频位置。模拟信号x(t)经过A/D转换后，得到离散的信号x0(n)，假设要观测的频带为f1～f2，则在此频带范围内进行细化分析，观测的中心频率为fe=(f1+f2)/2对x0(n)以e-j2πfe/fs进行复调制，得到的频移信号：

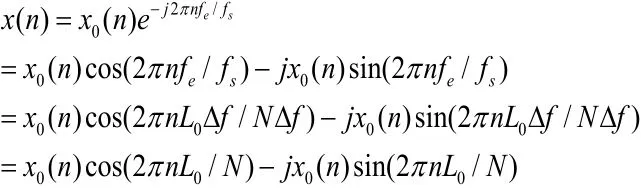
式中fs=NΔf为采样频率，Δf为谱线间隔，L0=fe/Δf为频率的中心移位，也是在全局频谱显示中所对应中心频率fe的谱线序号，则fe=L0Δf。由此可得出，复调制使x0(n)的频率成分fe移到x(n)的零频点，也就是说X0(k)中的第L0条谱线移到X(k)中零点频谱的位置。为了得到X(k)零点附近的部分细化频谱，可重新抽样把频率降到fs/D，D为细化倍数。为了是抽样后的频率不发生频谱混叠，需要在抽样前进行低通滤波。

(2)数字低通滤波

为了保证重新采样后的信号在频谱分析时不发生频谱混叠，需进行抗混叠滤波，滤出需要分析的频段信号，设细化倍数为D，则数字低通滤波器的截止频率fC≤fs/2D。

(3)重新抽样

信号经过移频、低通滤波后，分析信号点数变少，但再以较低的采样频率进行重新采样，在通过补零保证相同的采样点数时，样本的总长度加大，频谱的分辨率也就得到了提高。

设原采样频率为fs，采样点数为N，则频率分辨率为fs/N，现重采样频率为fs/D,当采样点数仍是N是，其分辨率为fs/(D*N)，分辨率提高了D倍。这样就在原采样频率不变的情况下得到了更高的频率分辨率。

(4)复数FFT

重新采样后的信号实部和虚部是分开的，需要对信号进行N点复FFT，从而得出N条谱线，此时分辨率为Δf′=fs′/N=fs/ND=Δf/D，可见分辨率提高了D倍。

(5)频率调整

经过算法运行后的谱线不为实际频率的谱线，需要将其反向搬移，转换成实际频率，进而得出细化后的频率。

3.ZOOMFFT的实现

目前我们用的芯片是STM32，在芯片上运行ZoomFFT算法程序，可直接调用STM32固件库，程序简单、稳定可靠、结构性强。STM32固件库有FIR滤波器，只要求出所需滤波器参数的系数，调用固件库的函数即可，计算既快又稳定，效率很高。FFT的实现是通过C语言编的FFT子函数，只要得到输入序列和FFT点数，调用FFT子函数就可求出FFT的输出序列。部分核心ZoomFFT的C语言程序如下：

mrelfft(adr,adi,N,-1);

//// /求幅频特性/////////

for(k=0;k＜N;k++)

{p=pow(adr[k],2)+pow(adi[k],2);

fft[k]=sqrt(p);}

//频率调整可通过公式实现f=fe+i*(fs/(D*1024.0));

4.实验结果

算法的验证通过两种方式进行了验证：函数信号发生器加入实际信号；在工程中实际测量。

(1)加实际信号。通过函数信号发生器加频率为55000Hz、幅值为1V和频率为55030Hz、幅值为0.7V的实际信号，得到的频谱如图2所示。

通过实验得出，未经过ZOOMFFT的信号，两个很接近的频率叠加到了一起，而经过ZoomFFT后的频谱在分辨率内可以分别，通过分析可得出ZoomFFT得到的信号频率比直接FFT得到的频率更真实，分辨率高、误差小、稳定性好。

(2)在工程中实验

将算法应用到测量设备中，测量物体动作时的返回频率，通过动态测量返回信号的频谱如图3所示。

由实验我们可以看出，函数信号发生器的信号是理想信号，测得频谱均为一根谱线，而实际测量中，由于有噪声的存在，测量的频谱不是一根谱线，而是一个峰，但峰顶的位置和实际频率一致，稍微的运动就可以从峰顶的位置反应出来。

实际的测量时，STM32通过外部AD进行采样，在其上只运行算法程序，约150毫秒，将移频时的三角函数的计算用数组表示，也就是将三角函数的值算出放在数组里，移频时直接调用数组，省去两次1024点的三角相乘计算的时间，用数组存放三角函数值后，算法程序耗时110毫秒。为降低，我们可测试了调用STM32固件库自带的汇编FFT，此时耗时约30毫秒，但STM32自带的FFT的输入输出都是32位整型，计算的精度没有C语言的浮点型变量FFT精度高。目前我们已经将该算法成功应用到了自己制作的水速测量算法中，并取得了理想的效果。

5.总结

通过实际的测量分析实现了对某频段的频谱细化分析，ZoomFFT在不增大FFT点数N的情况下降低了采样频率，提高了在细化频谱分析中有很重要的作用，可以通过此算法得到欲观测的频段局部频谱特性。由于计算量小，在实际应用中不需要用高速处理芯片，如我们应用的STM32足以满足其应用。可见ZoomFFT是一个行之有效的解决局部频段分析的方法。

[1]王世一.数字信号处理[M].北京:北京理工大学出版社(修订版),1997.

[2]胡广书.数字信号处理——理论、算法与实现[M].北京:清华大学出版社.1997.

[3]高怀钢,王华.一种分析频谱局部特性的快速算法[J].火控雷达技术,1999(3):14-17.

[4]江波,唐普英.基于复调制的ZoomFFT算法在局部频谱细化中的研究与实现[J].大众科技,2010(7):48-49.

[5]徐卓华.基于MATLAB的ZOOM FFT在水声测量中的应用[J].声学与电子工程,2004(4):13-16.