基于Lorenz系统提取数值模式可预报分量的初步试验

王启光 封国林 郑志海 支蓉 丑纪范

1 兰州大学大气科学学院，兰州 730000

2 国家气候中心气候研究开放实验室，北京 100081

基于Lorenz系统提取数值模式可预报分量的初步试验

王启光1封国林2郑志海2支蓉2丑纪范1

1 兰州大学大气科学学院，兰州 730000

2 国家气候中心气候研究开放实验室，北京 100081

针对数值预报模式中存在的非线性混沌特性，从提取可预报分量的思路出发，阐述了在数值模式中提取可预报分量的方法，并利用Lorenz系统进行了相关数值试验。研究发现，Lorenz系统初始误差在相空间中的增长速度是不同的，某些方向的误差增长速度较慢，即存在对初值扰动不敏感、相对稳定的可预报分量。根据数值模式切线性误差算子的特征值演化规律，提取出数值模式的可预报分量，并将模式变量在其基底上进行投影变换，建立了可预报分量数值模式。在此基础上，研究了Lorenz系统的混沌状态、模式参数误差及外部随机噪声对提取可预报分量的影响，发现基于可预报分量的数值模式，具有更好的预报技巧。

数值预报 可预报分量 奇异值分解 Lorenz系统

1 引言

大气是一个复杂的外有强迫、内有耗散的非线性巨系统，在太阳、海洋、陆地等外强迫因素的作用下，其内部发生一系列物理化学变化及相互作用，这为天气气候预测带来很大困难。早在1963年，Lorenz（1963）发现大气和其他不稳定动力系统类似，其可预报时效是有限的，他从流体的运动方程出发，通过简化方程获得了具有三个自由度的系统，并在计算机上用他所建立的微分方程模拟气候变化，意外地发现初始条件的极微小差别却可以引起模拟结果的巨大变化，这说明天气过程以及描述它们的非线性方程是如此的不稳定。基于此的研究工作 （Lorenz，1969，1982；Chou，1989；Ding and Li，2007；李建平和丁瑞强，2008；丁瑞强和李建平，2009）表明，逐日天气可预报时效的理论上限一般为2周，超过这个理论上限的天气预报被认为毫无准确率可言。然而，观测和动力理论研究均表明，即使在更长的时间尺度内，天气过程中仍然客观存在可预报的分量。例如，行星尺度的大气活动中心，其特征时间尺度往往比天气尺度更长；Chao et al.（1982）通过研究大气的非绝热耗散，发现了比Rossby波移动更慢的非绝热波，并认为它代表了半永久的活动中心，是长期数值天气预报的预报对象；基于MJO季节内振荡的热带高空环流场的预报时效可达30天 （李崇银等，2003；祝从文等，2004；陈光华和黄荣辉，2009；韩荣青等，2010；Ding et al.，2010，2011）。但数值预报模式与此相关的模拟预报能力还存在严重不足。一方面，随着观测技术的不断变革，观测资料日益丰富，加之资料同化、集合预报等方法的有效运用，使得模式的初始条件得到良好的改善。同时，数值预报模式中物理参数化方案的改进，计算机计算能力的提高等，从而使模式对实际大气行为的刻画更为具体，分辨率更高，这些对逐日数值天气预报的发展和水平的提高都做出卓有成效的贡献。另一方面，人们对中期和长期天气过程发生、发展的认识还很不充分，由于该过程是一个大气初值信息不断衰减，外部强迫影响逐步增强的过程，存在可预报源信息量不足的问题 （丑纪范，1974，1983；王鹏飞等，2009）。而且现有的数值模式和资料相对于大气的真实状态而言仍然十分粗糙，加之模式变量间的非线性相互作用以及计算误差等客观因素的影响 （庄照荣等，2010；李志强和俞永强，2011），致使利用数值预报模式进行长期天气预报仍存在很大困难。

当前，对较长时段的延伸期天气预报研究主要以统计手段为主，但这没有充分利用已掌握的物理规律，无法区分统计规律是本质的还是偶然的。在数值模式预报方面，由于初值和模式的不准确，使得预报误差在描述大气运动的非线性模式中不可避免地快速增长，数值延伸期预报的效果几近于随机情况。针对以上问题，丑纪范等 （2010）提出了提取数值模式中可预报分量的理论，将数值模式的状态变量分为可预报的稳定分量和不可预报的混沌分量，在预报过程中需要有针对性地采取不同的预报方案和策略。这有别于传统集合预报中寻找初始扰动发展最快方向的思路 （Ehrendorfer and Tribbia，1997；穆穆等，2007），只需对初始扰动不敏感的分量利用数值模式进行确定性预报，其余部分建议用历史资料给出概率分布，为改善数值模式的预报质量提供了一个全新的方向。郑志海 （2010）通过EOF分解压缩自由度的方法，在历史时空资料中分离出在实际大气和数值模式中均具有较强可预报性的分量，并利用历史资料信息对可预报分量进行相似误差订正，继而采取集合预报的方法，较好地提高了6～15天中长期数值预报技巧。但如何直接在数值模式中定量得到误差增长缓慢的基底，从而实现可预报分量提取的工作仍需进一步研究。

研究一种数值预报方法的有效性时，往往先从简单模式出发 （穆穆和段晚锁，2003；Feng and Dong，2003；任宏利，2006）。已有研究表明，三维Lorenz系统可以在某种程度上代表实际大气的一些特征（Anderson，1997），该模式已被广泛地应用于各种理论和方法研究中 （Gauthier，1992；封国林等，2009）。因此，本文选用Lorenz系统研究数值模式中可预报分量的提取过程，建立基于可预报分量的数值模式，探讨了初值扰动、系统混沌状态、模式误差和随机噪声对可预报分量模式的影响。

2 原理方法与模式介绍

2.1 提取可预报分量理论及方法

数值天气预报的本质是通过大气在一个时刻观测值求解刻画大气内部物理过程的动力学方程，从而由已知的初始时刻的大气状态预报未来时刻的大气状态。大气数值预报模式可以简化表示为：

其中，φ（x，t）为模式预报变量，x和t分别表示空间坐标和时间，H是φ的微分算子，对应于实际的数值模式。t0为初始时刻，φ0为初值。将 （1）式离散化后，可以得到一个非线性模式的解，它只依赖于初始条件：φT＝K（φ0），其中φ0∈Rn为初始时刻t0的近似真实的观测场，φT∈Rn为T时刻的预报场，K是数值模式根据初始条件到T时刻的积分。如果在初始场上加一个小扰动φ′0，则在时刻T有一个预报增量η，它们之间的非线性关系可表示为：

如果预报增量η对初始扰动φ′0不敏感，即满足O（η）～O（φ′0），则表明在时刻T，动力学方程对初值不敏感，是可预报的，反之则是不可预报的。当φ′0很小时，即‖φ′0‖≪‖φ0‖，那么根据 （2）式可得到预报增量与初始扰动的近似切线性关系：

其中，Lφ0，T为线性算子，它依赖于初始场φ0和预报时刻T，Rn空间的线性算子Lφ0，T即为一矩阵。它和传统的切线性模式不同，不再需要将数值模式演变的轨迹在每个时间间隔内都切线性化，而是将预报过程看成一个非线性映射K：Rn→Rn，不再考虑积分过程中的演变，认为预报误差增量是由于初始小扰动由非线性映射而来，Lφ0，T是对非线性映射的切线性化。由奇异值分解理论可知 （张永领等，2006），对任意向量L，存在两个正交矩阵U和V，

其中，

Λ是L的特征值 （λ1≤λ2≤…λn）组成的对角矩阵，U和V分别是L左、右特征向量组成的矩阵。每列ui、vi是Rn空间的一个向量，全体构成一组标准正交基，任一向量φ0（或φT）可按此基展开，一般称（u1，u2，…，un）为演化特征向量，（v1，v2…，vn）为初始特征向量。可以证明，对于特征值 （λ1≤λ2≤…λn），λp为 （1，2，…，p＜n）初始误差前p个分量的最大放大倍数，如果λp小于某个阈值，则可认为前p个分量对初值误差不敏感，是可以预报的，剩下的n－p个分量不可预报。

为确定前p个可预报分量，可以利用式（4）将切线性误差算子进行分解，根据误差增长情况取特征值λi较小时所对应的误差增长方向进行模式积分预报，而对于λi超过某一阈值对应的分量方向先行滤除，即可得到前p个可预报分量。对非线性数值预报模式而言，求解其切线性误差算子可以假设其非线性解为 （Kalnay，2005），

其中，K为模式根据初始时刻t0到t时刻的积分，可以在基本模式积分x（t）上加一个小扰动x′（t），则有

式 （6）中的x′（t）可以用和式 （5）同样的差分格式通过时间积分得到，当扰动较小时，此处可以看成，

其中，误差算子L（t0，t）＝∂K／∂x将初始时刻t0的扰动映射为t时的最终扰动。若忽略到扰动项中的二次项和更高阶项，

因此沿着n个单位向量x′i（t0）＝εei建立一个大小为ε的小扰动球作为初始扰动，以式 （8）进行计算，通过该方法选择初始扰动后，减去式 （5）即可得到线性误差算子矩阵。

2.2 Lorenz系统

Lorenz系统一般形式为：

考虑到物理背景，一般取δ＝10.0，b＝8／3，0＜r＜∞，令系统（9）左端为零，得到Lorenz系统的三个定常解 （王启光等，2008）：

当r＞24.74时，在整个相空间内不存在任何稳定的平衡态，这就是所谓的混沌状态。该状态仍然存在着一定的时空结构，即存在不同尺度的准周期特征。Lorenz系统处于混沌状态时具有初值敏感性、短期可预测性，长期不可预测性以及相空间遍历性。由于混沌系统对初值极其敏感，随着时间的演化，初值的微小差异会逐渐被放大，直至引起系统未来状态的显著不同，甚至得到完全相反的结果。

2.3 预报效果的检验统计量

对于Lorenz模式数值试验的预报结果检验有别于复杂数值预报模式的检验，后者主要关注预报误差场在空间型预报技巧的提高，而Lorenz模式的预报检验应更着重于预报的有效时间长度，当两个平衡态之间的转换报错了，预报误差就会突然增大到无技巧的状态，所以本文对Lorenz系统采用如下定义的相对预报误差 （任宏利，2006），

其中，T为预报时间，F代表预报，R代表实况。由大量的预报试验发现，当R（T）超过1.0时，预报就已经失效了，所以将此时对应的时间作为预报临界时间TC，到达该时刻后预报将失去意义。

3 误差增长及其算子特征值演化规律

本节选取Lorenz系统参数值为δ＝10.0，b＝8／3，r＝28.0，由于该系统对于z轴具有对称性，同时根据初值与不稳定平衡态的远近程度，分别选取初值 （1.0，－1.0，6.0）、（7.0，7.0，25.0）、（9.0，9.0，27.0）进行积分数值试验，简记 为INI1、INI2、INI3。运用数值计算的方法，采用积分步长为0.01，积分30个时间单位，得到样本量为3000的三维时间序列，一般可认为1个时间单位对应实际大气演化过程中的5天，即每20步积分相当于1天 （任宏利，2006）。为研究Lorenz系统误差增长情况，首先分别对三个不同初值的三个方向添加ε≤0.01的球形扰动作为初始误差集，初值扰动点的个数为20000个，得到的初值误差演化如图1所示。

图1中展示了模式初始状态、模式演化10步、模式演化1000步、模式演化2000步四个不同的状态。图1a、e、i分别代表INI1、INI2、INI3条件下，添加球形随机扰动时，模式初始误差场在相空间中的分布。初始时刻，相空间中的模式误差限制在初值点周围半径为0.01的球形区域范围内。从图1可以发现，在同一个初值条件下，随着积分时间的增加，初始的微小误差在不同方向增长速度明显不同，误差场扰动球的形状逐渐由球形变为椭球，有的方向误差快速增长，误差范围逐步扩大，而另外一些方向误差缓慢增长甚至收缩，随积分时间的进一步增加，误差在相空间中的结构变为弯曲的线状，并最终扩散到整个相空间的吸引子上。例如当初值为INI1时，积分时间到第10步 （图1b），误差在x－y平面投影变为长椭圆，值域的范围约为0.08，在x－y平面的对角线方向误差明显变大，而在x－z和y－z平面上的投影仍是圆形，值域范围基本保持初始状态0.02不变；当积分步长达到1000时 （图1c），误差在x－y、x－z、y－z三平面投影范围分别约为1.5、3、4，比初值误差范围都增大了数百倍，可以推断，此时模式变量的演化曲线将发生明显的分离，模式变量将变的不可预报；当积分步长为2000时 （图1d），最大相差0.02的初值误差场，已经遍布整个相空间吸引子中，起始时刻的球形扰动误差已变为典型的 “蝴蝶”形状，误差值域范围比初始状态扩大了数千倍。图1还表明，相同值域范围的初始扰动在不同的初值条件下，其误差发展速度明显也是不同的，例如，初值为INI3，积分10步时在各个平面投影的值域范围基本维持在0.02（图1j），在x－y和x－z平面中投影变为椭圆；当积分步长为1000时 （图1k），误差在x－y、x－z、y－z平面投影范围分别约为0.04，0.06，0.06，比初始误差值仅增长了几倍，可以推断，此时模式变量的演化曲线基本还是相吻合的，模式的可预报性仍然存在；当积分步长为2000步时，相空间中误差场形状变为长椭球状 （图1l），因此误差在某些方向增长仍然较小，模式仍存在一定的可预报性。初值为INI2时，误差增长的速度在各方向也是不同的，在相同演化步长时，其误差增长比INI3条件下快，而比INI1慢 （图1eh）。比较三初值条件下误差演化的情况，可以发现数值模式的预报过程中，客观存在误差增长相对缓慢的可预报分量。研究结果还表明模式误差的发展速度和初值所处相空间中的位置直接有关，这同已有的研究结论是吻合的 （Zou et al.，2006）。

为研究随机扰动量级对误差演化的影响，将上面的扰动范围增大10倍，即ε≤0.1，在INI2条件下误差演化结果如图2（见文后彩图）所示。比较图2a－d和图1e－h，虽然初值扰动的量级明显增大，但相空间中误差的演化仍然呈现某些方向增长快，而另外一些方向增长慢的状态，并且误差增长方向和速度基本与ε≤0.01时相同。这进一步说明误差增长较慢的可预报分量与数值模式内在的固有属性有关，在相似的初值条件下的可预报分量，具有相似的演化规律，为可预报分量的提取及其应用提供了良好的物理基础。

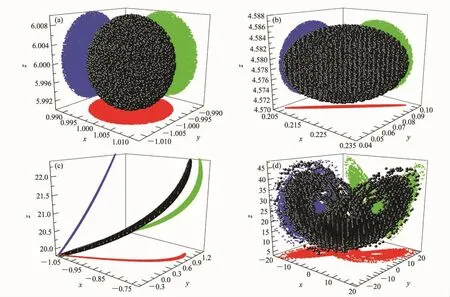
图1 （a－d）INI1、（e－h）INI2、（i－l）INI3添加随机扰动ε≤0.01误差演化情况：（a、e、i）初始状态；（b、f、j）10步；（c、g、k）1000步；（d、h、l）2000步Fig.1 The evolution of the errors under different initial values marked by（a－d）INI1，（e－h）INI2，（i－l）INI3when random perturbation was added to the Lorenz system with errorε≤0.01：（a，e，i）The initial status；（b，f，j）the evolution steps are 10；（c，g，k）the evolution steps are 1000；（d，h，l）the evolution steps are 2000

图1 （续）

基于以上模式误差增长规律的分析，下面分别就INI1、INI2、INI3条件下，将Lorenz模式各变量误差分别取0.01和0.1时，利用式 （1）～（9）计算出切线性误差算子L，进而得到特征值λi随积分时间的演化曲线 （如图3所示）。

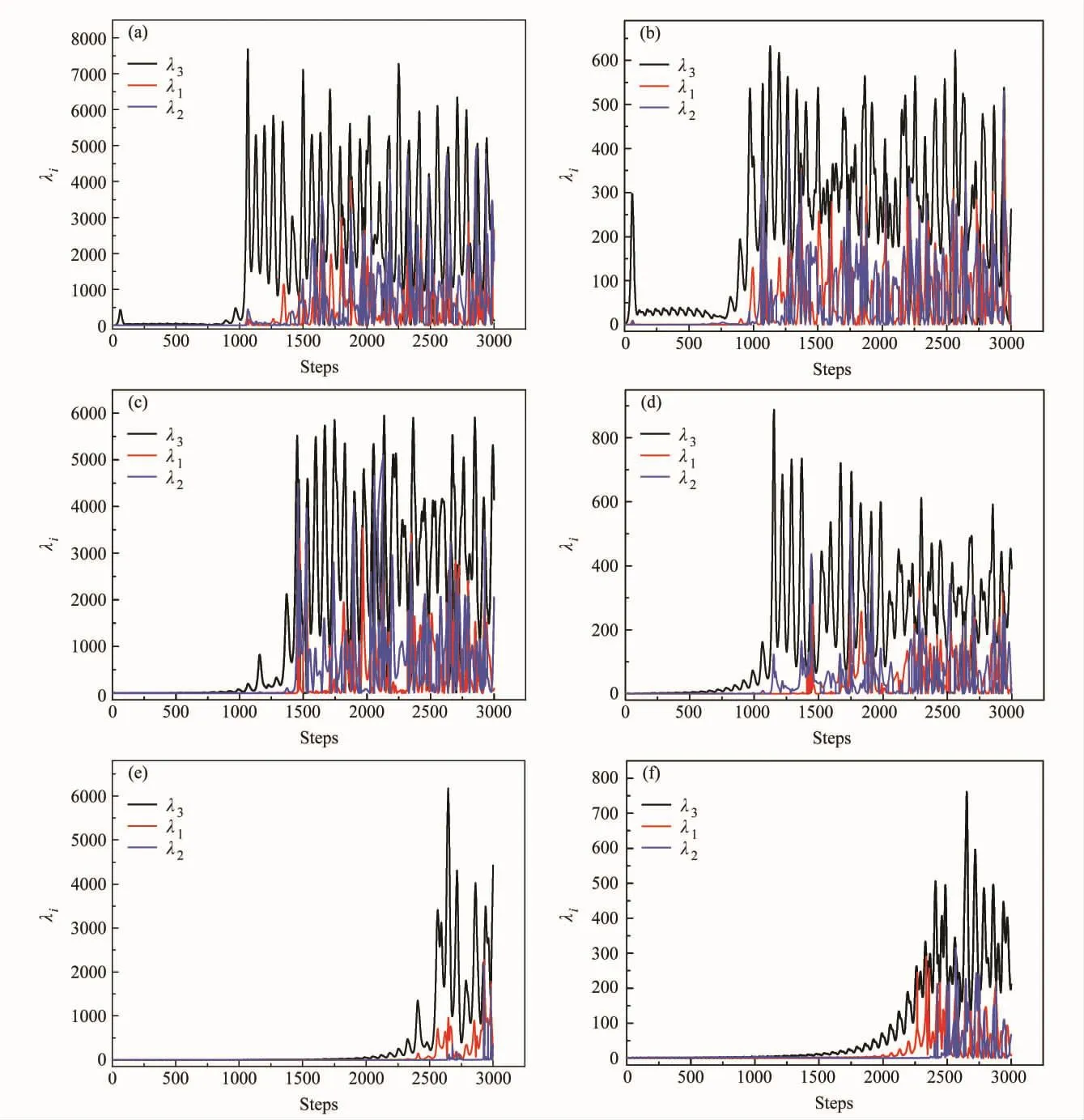
从图3中可以看出，切线性误差算子L的特征值λi随积分时间的增长差别明显，反映出初始误差在初始向量的不同方向上增长的速度不同这一特性。在初值INI1、ε＝0.01条件下，λ3在短时间内增长迅速，在积分50步后其演化轨迹即与λ1、λ2分离 （图3a），而λ1、λ2此时基本维持在 （0，1）之间，积分时间达到1500步以后，λ1、λ2、λ3都显著增大，表明此时模式变量误差在各个方向都明显增长，模式中基本无可预报分量而言，系统完全进入混沌状态，误差在相空间中的分布类似于图1d；当ε＝0.1时λ3迅速增长的状态更为明显，λ3在50步时即接近300，表示初始向量空间中，该方向上误差增长迅速。当初值为INI2、ε＝0.01时，λ3在积分1000步后才开始明显增长，将达到1500步时λ1、λ2、λ3都开始增大，但是λ1、λ2增长的量级比λ3小得多；ε＝0.1时，λ3在积分500步即快速增长，而λ1、λ2在1000步以内基本未增长，在1400步左右时三者才都快速增长。初值INI3的切线性误差算子特征值比其他两种初值情况增长的都缓慢，在ε＝0.01、0.1条件下，λ3分别在2000步和1500步后发生分离，λ1和λ2迅速增长的时间都要明显靠后。由第2节可知，λi的值反映了初始误差在初始向量对应方向上的增长倍数，Lorenz系统在非线性演化过程中误差增长在不同方向上的差别，为从初始向量基底上提取模式变量的可预报分量提供了可能。

进一步，以初值INI2为例，模式各变量分别添加ε＝0.01和ε＝0.1的初始扰动，对模式积分500步以内得到的L进行奇异向量分解，得到的特征值演化如图4（见文后彩图）所示。从图4中可以看出特征值λi在各方向上的增长在模式演化初期基本一致且都在 （0，1）之间，随着时间的增长，λ3逐渐增大，对应了相空间中误差演化的伸长方向，λ1趋向于0，对应了误差演化的收缩方向。λ2基本维持在1附近，说明该方向误差基本不增长。同时还可以发现，虽然添加扰动的量级不同，但两种情况下λ3都是在190步左右和λ1、λ2发生分离并开始缓慢增长。因此本文考虑误差增长规律，选取λ3＞2时对初始特征向量中该方向的分量予以滤除，仅保留其余两个方向分量，得到稳定分量基底，从而建立可预报分量模式。

4 提取可预报分量及敏感性试验

4.1 可预报分量模式的建立

可预报分量模式的建立可以通过以下途径实现，在积分过程中将模式变量投影到可预报稳定分量的基底上，再利用矩阵逆变换得到针对可预报分量的模式变量，然后向前积分，依次逐步变换积分即可。在已有的模式基础上进行改进，无需开发新模式，使用方便且可移植性强。其过程可简要表示

如下：

其中，A为数值模式稳定分量投影基底，φ为模式变量，为模式变量在可预报分量上的投影。设K为数值模式的积分算子，稳定分量的预报方程即为，

基于以上过程，表1比较了Lorenz系统原始变量模式和建立的可预报分量模式的TC。

表1 不同初值和扰动条件下Lorenz系统原始变量及可预报分量的TCTable 1 The prediction times（TC）of original variables and predictable components in Lorenz system under different initial values and perturbations

从表1中可以看出在三个不同初值条件下，对初值各变量分别进行大小为0.01和0.1的扰动，可预报分量的TC都要明显大于原始变量，具有更高的预报技巧。并且在同一初值条件下，初值扰动量级越大，TC则越小。由表1可以得出，对数值模式中误差增长慢的可预报分量进行预报，可以得到比原始变量模式更长的可预报时效。

4.2 控制参数变化对可预报分量模式的影响

对于Lorenz系统而言，当系统控制参数r增大时，系统动力学结构的混沌特性将更加明显，可预报性随之降低。为进一步研究提取可预报分量在非线性数值模式预报中的有效性，图5以初值INI2、ε＝0.1为例，研究了TC在原始变量模式和可预报分量模式中随着控制参数的变化情况。在控制参数从28以0.1的间隔逐步增大到30过程中，Lorenz系统原始变量模式的TC随着控制参数的增大，由11.14减小到5.65，呈明显的衰减趋势。而可预报分量的TC在此过程中始终比原始变量的大，并且没有明显的下降趋势，这说明提取的可预报分量的TC并不随系统的混沌特征明显而衰减，有较好的可预报价值。

图5 TC随控制参数的演化情况 （“orig”代表原始变量；“pred”代表可预报分量）Fig.5 The evolution of TCwith parameter r （“orig”：original variable；“pred”：predictable component）

4.3 模式误差及外部噪声影响

一般而言，数值模式误差主要可分为初值误差和模式误差两个方面。初值误差又可分为观测误差和分析误差；模式误差的来源较多，包括数值计算的截断误差、参数不准、物理过程缺失、动力方程缺陷、物理参数化方案缺陷等。因此，通过原始变量模式建立起的可预报分量模式，既要考虑到初值误差的影响，又要考虑模式误差存在时，可预报分量模式建立的有效性。本节以初值INI2、ε＝0.1为例，研究了分别对Lorenz模式参数b和积分过程变量中添加δ≤0.01的球形随机扰动情况，扰动次数为20000次，结果如表2所示。当对模式参数b进行随机扰动时，其原始变量模式TC最小值为7.61，最大值为11.14，历次扰动后TC的平均值为9.65。相同条件下可预报分量模式对应的值分别为9.07、14.72和11.82。当在积分过程变量中加入随机扰动时，其原始变量模式TC最小值为8.96，最大值为11.13，历次扰动后TC的平均值为10.29。相同条件下可预报分量模式对应的值分别为10.18、14、69和12.46。从扰动后的TC均值来看，可预报分量模式的预报效果仍然要优于原始变量模式，说明可预报分量模式在一定时间段内，不仅对初值误差不敏感，而且受模式变量误差的影响也比原始变量模式小。

表2 模式误差及外部随机噪声对TC的影响Table 2 The effects of model errors and external random noises on prediction time TC

5 结论和讨论

本文从提取数值模式的可预报分量出发，利用Lorenz系统进行了相关数值试验。通过研究误差在相空间中的增长状况，得知初始误差在不同方向增长速度不同，误差增长的不均匀性代表在一定时间范围内，数值预报模式中客观存在着对误差不敏感的较稳定的可预报分量。采用不同量级的初值扰动，研究了模式切线性误差算子特征值的演化规律，结果表明在初始特征向量的三个方向上，有一个方向误差增长速度明显较快，在很大程度上影响着数值预报模式的可预报时效。进而对该方向在积分过程进行滤除，建立了基于可预报分量的新模式。比较了不同初值条件下原始变量模式和可预报分量模式的预报临界时间，发现可预报分量模式预报临界时间比相同条件下原始变量的要长，说明其有更高的预报技巧。通过改变模式的控制参数，发现可预报分量模式受控制参数变化影响小。最后对数值模式变量进行了扰动，并试验了随机噪声对可预报分量模式和原始变量模式的影响。发现可预报分量模式比原始变量模式预报时效长，说明提取可预报分量方法在数值预报过程中，有潜在的应用价值。在本文的研究过程中还发现，在不同的初值条件下，可预报分量模式延长的可预报时间是不同的，这反映了对于Lorenz系统而言，可预报分量模式的效果可能受系统局地可预报性的影响，当系统初始状态处于可预报性较高区域，模式预报误差在各个方向发展速度均较慢，可预报分量模式相应的可预报时间将更长，反之则相反。并且可预报分量模式的预报效果还可能与初始误差的大小存在一定关系，这些问题还需要在后继工作中深入探讨。本文仅利用简单模式阐述了在数值模式中提取可预报分量的方法及其效果，在复杂模式中的应用及其可能存在的困难我们将在下一步工作中予以研究和解决。

（References）

Anderson J L.1997.The impact of dynamical constraints on the selection of initial conditions for ensemble predictions：Low－order perfect model results［J］.Mon.Wea.Rev.，125 （11）：2969－2983.

Chao J P，Guo Y F，Xin R N.1982.A theory and method of longrange numerical weather forecasts［J］.J.Meteor.Soc.Japan，60：282－291.

丑纪范.1974.天气数值预报中使用过去资料的问题 ［J］.中国科学 （A 辑），（6）：635－644. Chou Jifan.1974.A problem of using past data in numerical weather forecasting［J］.Science in China（Ser.A）（in Chinese），（6）：635－644.

丑纪范.1983.初始场作用的衰减与算子的特性 ［J］.气象学报，41（4）：385－392. Chou Jifan.1983.Some properties of operators and the effect of initial condition［J］.Acta Meteorologica Sinica（in Chinese），41（4）：385－392.

Chou J F.1989.Predictability of the atmosphere［J］.Advances in Atmospheric Sciences，6（3）：335－346.

丑纪范，郑志海，孙树鹏.2010.10－30d延伸期数值天气预报的策略思考——直面混沌 ［J］.气象科学，30（5）：569－573. Chou Jifan，Zheng Zhihai，Sun Shupeng.2010.The think about 10－30 d extended－range numerical weather prediction strategy—facing the atmosphere chaos［J］.Scientia Meteorologica Sinica（in Chinese），30（5）：569－573.

Ding R Q，Li J P.2007.Nonlinear finite－time Lyapunov exponent and predictability［J］.Physics Letters A，364：396－400.

丁瑞强，李建平.2009.非线性误差增长理论在大气可预报性中的应用 ［J］.气象学报，67（2）：241－249. Ding Ruiqiang，Li Jianping.2009.Application of nonlinear error growth dynamics in studies of atmospheric predictability［J］.Acta Meteorologica Sinica（in Chinese），67（2）：241－249.

Ding R Q，Li J P，Seo K H.2010.Predictability of the Madden－Julian oscillation estimated using observational data ［J］.Mon.Wea.Rev.，138（3）：1004－1013.

在广州车展开始之前，由于梅赛德斯-AMG G 63先型特别版试驾车的到位，我和摄影师还有他的朋友腾出了两天时间，从北京出发，行经300公里的高速路段，穿过了最近一年新闻联播中颇为著名的塞罕坝景区，来到了位于内蒙古，早已是一片白雪皑皑的乌兰布统。红山军马场，这个听起来有些浪漫又有些严肃的地名就是这一次我们一行三人的最终目的地，在凛冽的北风中，这片草原的主人早已不是那些听话且健壮的军马，取而代之的是洁白的积雪和偶尔代表着人类文明的深浅不一的车辙。

Ding R Q，Li J P，Seo K H.2011.Estimate of the predictability of boreal summer and winter intraseasonal oscillations from observations［J］.Mon.Wea.Rev.，139：2421－2438，doi：10.1175／2011MWR3571.1.

Ehrendorfer M，Tribbia J J.1997.Optimal prediction of forecast error covariances through singular vectous［J］.J.Atmos.Sci.，54（2）：286－313.

Feng G L，Dong W J.2003.Evaluation of the applicability of a retrospective scheme based on comparison with several difference schemes［J］.Chinese Physics，12：1076－1086.

封国林，王启光，侯威，等.2009.气象领域极端事件的长程相关性［J］.物 理 学 报，58 （4）：2853－2861. Feng Guolin，Wang Qiguang，Hou Wei，et al.2009.Long－range correlation of extreme events in meterorological field［J］.Acta Physica Sinica（in Chinese），58（4）：2853－2861.

Gauthier P.1992.Chaos and quadri－dimensional data assimilation：A study based on the Lorenz model［J］.Tellus（Ser.A），44：2－17.

韩荣青，李维京，董敏.2010.副热带北太平洋大气季节内振荡时空特征的诊断研究 ［J］.气象学报，68 （4）：520－528. Han Rongqing，Li Weijing，Dong Min.2010.A diagnostic study of the temporal and spatial characteristics of the intraseasonal oscillation over the subtropical northern Pacific［J］.Acta Meteorologica Sinica（in Chinese），68（4）：520－528.

Kalnay E.2005.大气模式、资料同化和可预报性 ［M］.蒲朝霞，杨福全，邓北胜，等，译.北京：气象出版社，178－190.Kalnay E.2005.Atmospheric Modeling，Data Assimilation and Predictability（in Chinese）［M］.Translated by Pu Zhaoxia，Yang Fuquan，Deng Beisheng，et al.Beijing：China Meteorological Press，178－190.

李崇银，龙振夏，穆明权.2003.大气季节内振荡及其重要作用［J］.大气科学，27（4）：518－535. Li Chongyin，Long Zhen－xia，Mu Mingquan.2003.Atmospheric intraseasonal oscillation and its important effect［J］.Chinese Journal of Atmospheric Sciences（in Chinese），27（4）：518－535.

李建平，丁瑞强.2008.短期气候可预报期限的时空分布 ［J］.大气科学，32 （4）：975－986. Li Jianping，Ding Ruiqiang.2008.Temporal－spatial distributions of predictability limit of short－term climate［J］.Chinese Journal of Atmospheric Sciences （in Chinese），32（4）：975－986.

李志强，俞永强.2011.耦合模式热带太平洋云—气候反馈模拟误差评估 ［J］.大气科学，35（3）：457－472. Li Zhiqiang，Yu Yongqiang.2011.Assessment of cloud－climate feedback simulation bias of coupled ocean－atmosphere model in the tropical Pacific［J］.Chinese Journal of Atmospheric Sciences（in Chinese），35（3）：457－472.

Lorenz E N.1963.Deterministic non－periodic flow［J］.J.Atmos.Sci.，20：130－141.

Lorenz E N.1969.The predictability of a flow which possesses many scales of motion［J］.Tellus，21：289－307.

Lorenz E N.1982.Atmospheric predictability experiments with a large numerical model［J］.Tellus，34：505－513.

穆穆，段晚锁.2003.ENSO可预报性研究的一个新方法：条件非线性最优扰动 ［J］.科学通报，48（7）：747－749. Mu Mu，Duan Wansuo.2003.A new method of ENSO predictability：conditional nonlinear optimal perturbation［J］.Chinese Science Bulletin（in Chinese），48（7）：747－749.

穆穆，王洪利，周菲凡.2007.条件非线性最优扰动方法在适应性观测研究中的初步应用 ［J］.大气科学，31（6）：1102－1112.Mu Mu，Wang Hongli，Zhou Feifan.2007.A preliminary application of conditional nonlinear optimal perturbation to adaptive observation［J］.Chinese Journal of Atmospheric Sciences （in Chinese），31（6）：1102－1112.

任宏利.2006.动力相似预报的策略和方法 ［D］.兰州大学博士学位论文. Ren Hongli.2006.Strategy and methodology of dynamical analogue prediction ［D］.Ph.D.dissertation（in Chinese），Lan Zhou University.

王启光，支蓉，张增平.2008.LORENZ系统长程相关性研究 ［J］.物理 学 报，57 （8）：5343－5350. Wang Qiguang，Zhi Rong，Zhang Zengping.2008.The research on long range correlation of Lorenz system ［J］.Acta Physica Sinica（in Chinese），57（8）：5343－5350.

王鹏飞，李建平，顾雷.2009.气候数值模拟研究中初始场衰减理论的理解和应用 ［J］.气象学报，67（2）：218－226. Wang Pengfei，Li Jianping，Gu Lei.2009.Understanding and application of the decay theory of initial condition effect in numerical climate simulation studies［J］.Acta Meteorologica Sinica（in Chinese），67（2）：218－226.

张永领，吴胜安，丁裕国，等.2006.SVD迭代模型在夏季降水预测中的应用 ［J］.气 象 学 报，64 （1）：121－128.Zhang Yongling，Wu Sheng'an，Ding Yuguo，et al.2006.Forecast of summer precipitation based on SVD iteration model［J］.Acta Meteorologica Sinica（in Chinese），64（1）：121－128.

郑志海.2010.基于可预报分量的6－15天数值天气预报业务技术研究 ［D］.兰州大学博士学位论文.Zheng Zhihai.2010.Operational technology research of 6－15days numerical weather prediction based on predictable components［D］.Ph.D.dissertation（in Chinese），Lan Zhou University.

祝从文，Nakazawa T，李建平.2004.大气季节内振荡对印度洋—西太平洋地区热带低压／气旋生成的影响 ［J］.气象学报，62（1）：42－50. Zhu Congwen，Nakazawa T，Li Jianping.2004.Modulation of tropical depression／cyclone over the Indian－western Pacific Oceans by Madden－Julian oscillation［J］.Acta Meteorologica Sinica（in Chinese），62（1）：42－50.

庄照荣，薛纪善，李兴良，等.2010.GRAPES全球模式的模式误差估计 ［J］.大气科学，34（3）：591－598. Zhuang Zhaorong，Xue Jishan，Li Xingliang，et al.2010.Estimation of model error for the global GRAPES model［J］.Chinese Journal of Atmospheric Sciences（in Chinese），34（3）：591－598.

Zou M W，Feng G L，Gao X Q.2006.Sensitivity of intrinsic mode functions of Lorenz system to initial values based on EMD method［J］.Chinese Physics，15（6）：1384－1390.

图2 初值条件为INI2且ε≤0.1时误差演化情况：（a）初始状态；（b）10步；（c）1000步；（d）2000步Fig.2 The evolution of errors under initial value INI2with errorε≤0.1：（a）The initial status；（b）the evolution steps are 10；（c）the evolution steps are 1000；（d）the evolution steps are 2000

图4 INI2条件下L特征值λi前500步的演变：（a）ε＝0.01；（b）ε＝0.1Fig.4 The same as Fig.3，but for the first 500steps with initial value INI2when（a）ε＝0.01and（b）ε＝0.1

The Preliminary Analysis of the Procedures of Extracting Predicable Components in Numerical Model of Lorenz System

WANG Qiguang1，FENG Guolin2，ZHENG Zhihai2，ZHI Rong2，and CHOU Jifan1

1CollegeofAtmosphericSciences，LanzhouUniversity，Lanzhou730000
2LaboratoryforClimateStudies，NationalClimateCenter，ChinaMeteorologicalAdministration，Beijing100081

The authors have proposed to extract the predictable components to make prediction in the numerical model which has nonlinear chaos.The method of extracting predicable components was introduced in a simple numerical model，and the numerical experiments were done based on Lorenz system.In the experiment，the authors found that the velocity of initial error increase is different for different components in the phase space，and there are some particular directions with slow error increase.That is to say，there exist predictable components which are relatively stable and insensitive to initial perturbation.The numerical model of the predictable components was established by extracting predicable components based on the evolution of the eigenvalues of the tangent operator error，and projecting the model variables onto the substrates.On the basis of these，the impacts of chaotic states，the errors of model parameters，and the external random noise on extracting the predicable components were studied.And the authors found that the numerical model of the predicable components has a better forecasting skill.

numerical prediction，predictable components，singular value decomposition，Lorenz system

1006－9895（2012）03－0539－12

P435

A

10.3878／j.issn.1006－9895.2011.11094

王启光，封国林，郑志海，等.2012.基于Lorenz系统提取数值模式可预报分量的初步试验 ［J］.大气科学，36（3）：539－550，

10.3878／j.issn.1006－9895.2011.11094.Wang Qiguang，Feng Guolin，Zheng Zhihai，et al.2012.The preliminary analysis of the procedures of extracting predicable components in numerical model of Lorenz system ［J］.Chinese Journal of Atmospheric Sciences（in Chinese），36（3）：539－550.

2011－05－23，2011－06－24收修定稿

国家自然科学基金资助项目40930952、41105070和41105055，全球变化重大研究计划2012CB955902和公益性行业 （气象）科研专项GYHY201106016

王启光，男，1981年出生，博士研究生，主要从事短期气候预测研究。E－mail：photon316＠163.com

封国林，E－mail：fenggl＠cma.gov.cn